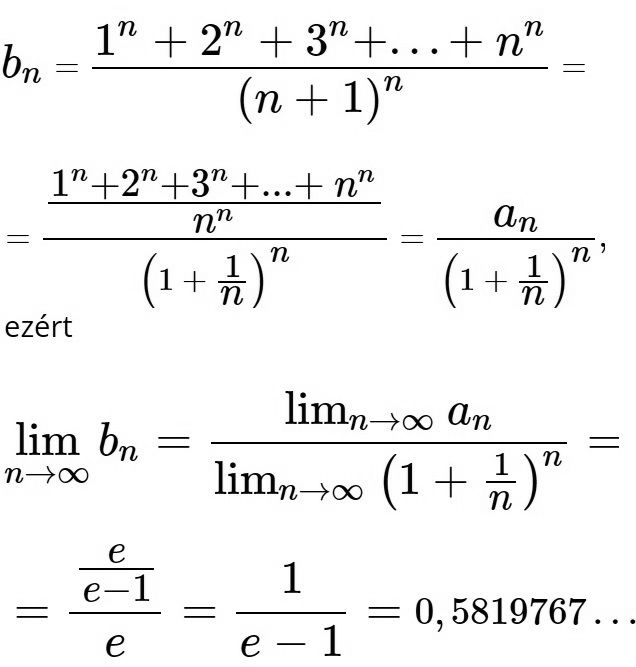Az alábbi rész kérdőjeles:
\(\displaystyle \lim_{n\to\infty}\Bigg(\frac{n}{n+1}\Bigg)^n+\Bigg(\frac{n-1}{n+1}\Bigg)^n+\Bigg(\frac{n-2}{n+1}\Bigg)^n+\Bigg(\frac{n-3}{n+1}\Bigg)^n+\dots ?= e^{-1}+e^{-2}+e^{-3}+e^{-4}+\dots\)
Ha \(\displaystyle b_n=\Bigg(\frac{n}{n+1}\Bigg)^n+\Bigg(\frac{n-1}{n+1}\Bigg)^n+\dots+ \Bigg(\frac{1}{n+1}\Bigg)^n\)
akkor attól még, hogy a tagok "függőlegesen" konvergálnak, tehát hogy fix k-ra
\(\displaystyle \lim_{n\to\infty}\Bigg(\frac{n-k}{n+1}\Bigg)^n=e^{-k-1}\)
még nem következik, hogy az \(\displaystyle e^{-k-1}\) határértékek összege megegyezik \(\displaystyle b_n\) határértékével. Az még elmondható, hogy \(\displaystyle b_n\) egy felső korlátja a mértani sor - bár már ehhez is hozzá kéne tenni , hogy ez a fenti limesz monotonitása miatt van - de hogy oda konvergál-e, az nem következik az általad leírtakból.
Ha \(\displaystyle b_{n,k}=\Bigg(\frac{n-k}{n+1}\Bigg)^n\) ha \(\displaystyle 0\leq k \leq n\) és \(\displaystyle b_{n,k}=0\) ha \(\displaystyle k>n\), akkor azt állítod, hogy
\(\displaystyle \lim_{n\to\infty}\sum_{k=0}^nb_{n,k}=\lim_{n\to\infty}\sum_{k=0}^\infty b_{n,k}=\sum_{k=0}^\infty(\lim_{n\to\infty}b_{n,k})\)
Viszont a fenti határátmenet csere nem nyilvánvaló.
A "szabályos" eljárás az, ami sakkmath 2. megoldásában van (Tannery-tétel). A képletek (indexek) egyszerűbbek lesznek, ha sakkmath megoldását követve a \(\displaystyle \lim_{n\to\infty}\sum_{k=1}^{n}\left(\frac{k}{n}\right)^n=\lim_{n\to\infty}S_n\) határértékét számoljuk először ki, aztán osztjuk e-vel.
Minden \(\displaystyle n\geq1\) esetén legyen:
\(\displaystyle a_{n,k}=\Bigg\{\begin{matrix}\bigg(\frac{n-k}{n}\bigg)^n & 0\leq k\leq n \\ 0 & k> n \\ \end{matrix}\).
Ez egy végtelen mátrix, aminek a főátlójában - kivéve az \(\displaystyle a_{1,0}\) -és felette minden elem 0, a nulladik (azaz az első) oszlop csupa 1-es.
Bármely fix k-ra ismert, hogy az \(\displaystyle a_{n,k}\) sorozat monoton növekvő és határértékére
\(\displaystyle \lim_{n\to\infty}a_{n,k}=e^{-k} \tag{1}\)
Legyen \(\displaystyle \varepsilon>0\) rögzített. Mivel \(\displaystyle \sum_{k=0}^{\infty}e^{-k}=\frac{e}{e-1}=S\), ezért létezik K, hogy
\(\displaystyle \sum_{k=0}^{K}e^{-k}>S-\varepsilon \tag{2}\)
Másrészt (1)-ben a monotonitás miatt
létezik \(\displaystyle N_0\), hogy \(\displaystyle n>N_0\) esetén \(\displaystyle 1-a_{n,0}<\frac\varepsilon {K+1}\)
létezik \(\displaystyle N_1\), hogy \(\displaystyle n>N_1\) esetén \(\displaystyle \frac1{e}-a_{n,1}<\frac\varepsilon {K+1}\)
...
létezik \(\displaystyle N_K\), hogy \(\displaystyle n>N_K\) esetén \(\displaystyle \frac1{e^K}-a_{n,K}<\frac\varepsilon {K+1}\)
Így, ha \(\displaystyle N:=\max(K,N_0,...,N_K)\), akkor összeadva a fenti K+1 darab egyenlőtlenséget, \(\displaystyle n>N\) esetén teljesül
\(\displaystyle \sum_{k=0}^{K}e^{-k}-\sum_{k=0}^{K}a_{n,k}<\varepsilon\)
Felhasználva (2)-t is:
\(\displaystyle \varepsilon>\sum_{k=0}^{K}e^{-k}-\sum_{k=0}^{K}a_{n,k}>
S-\varepsilon-\left(\sum_{k=0}^{n}a_{n,k}-\sum_{k=K+1}^{n}a_{n,k}\right)>S-\varepsilon-\sum_{k=0}^{n}a_{n,k}=S-S_n-\varepsilon\)
Azaz \(\displaystyle S-S_n<2\varepsilon\)
|