KöMaL Problems in Mathematics, December 2011
Please read the rules of the competition.
Show/hide problems of signs:
 |
Problems with sign 'K'Deadline expired on January 10, 2012. |
K. 313. Zsolti has nine identical drinking glasses. If one glass is placed onto another, the following different results are possible: If two tops or two bottoms touch, the two glasses will stay in that position. If a top meets a bottom, one glass will slide into the other and the combined height of the two glasses will be one and a half times the height of a glass. Zsolti is making a tower of glasses. He starts by arranging the nine glasses on the table in a 3×3 pattern, all with their tops facing upwards. Then he takes one row or column of glasses at the edge of the arrangement and places them, inverted, onto the glasses of the adjacent row or column. Thus he obtains a 2×3 arrangement. Then he inverts one of the rows or columns at the edge onto the adjacent one again, and so on, until a single tower of glasses is built. What may be the height of the tower?
(6 pont)
solution (in Hungarian), statistics
K. 314. The midpoint of the line segment AQ in the diagram is P, the midpoint of line segment BR is Q, the midpoint of CP is R, the midpoint of PL is K, and the midpoint of RM is L. Given that the area of triangle ABC is 441 cm2, find the area of triangle KLM.
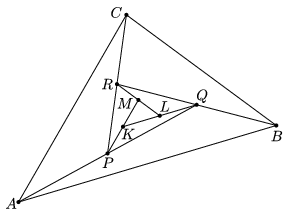
(6 pont)
solution (in Hungarian), statistics
K. 315. Let denote the greatest prime number smaller than n, and let
denote the smallest prime greater than n. Calculate the value of the expression
.
(6 pont)
solution (in Hungarian), statistics
K. 316. Find all common fractions that make a total of exactly 1 if added to 12/96, such that every digit occurs exactly once in the numerators and denominators of the two fractions together.
(6 pont)
solution (in Hungarian), statistics
K. 317. What may be the number of acute angles among the interior angles of a convex polygon?
(6 pont)
solution (in Hungarian), statistics
K. 318. Prove that if a, b, c, d are consecutive natural numbers, then d2 is a factor of the sum a+b2+c3.
(6 pont)
 |
Problems with sign 'C'Deadline expired on January 10, 2012. |
C. 1100. Fill in the appropriate fields of the table with numbers, such that, with the numbers given in the table, consecutive terms of geometric sequences are obtained in every row and in every column.
(5 pont)
solution (in Hungarian), statistics
C. 1101. We bought some packets of nine dice. In order to build a solid cube, we needed to open each packet. How many dice may have been left?
(5 pont)
solution (in Hungarian), statistics
C. 1102. D is the foot of the altitude drawn from vertex C of an acute-angled triangle ABC. Construct that line parallel to AB whose segment inside the triangle subtends a right angle at D.
(Suggested by G. Holló, Budapest)
(5 pont)
solution (in Hungarian), statistics
C. 1103. Gábor multiplied two positive numbers together, and found it interesting that the result was the same as the sum of the two numbers. He has forgotten the numbers themselves, but he can remember that they contained a single decimal digit each. What may be the numbers?
(5 pont)
solution (in Hungarian), statistics
C. 1104. Every angle of a hexagon is 120o, and the lengths of its sides are and
, alternating. Prove that the area of the hexagon is an integer.
(5 pont)
 |
Problems with sign 'B'Deadline expired on February 10, 2012. |
B. 4402. A white circle is inscribed in a dark unit square (see the figure). A dark square is inscribed in the circle, and the process is continued to infinity. What is the total of the dark areas?

(3 pont)
solution (in Hungarian), statistics
B. 4403. There are chessmen standing on some fields of a 20×20 chessboard. The rule is that a chessman can be removed from the board if at least a half of the fields is vacant in its row or in its column. What is the maximum possible number of chessmen on the board if all of them can be removed in a sequence of such steps?
(5 pont)
solution (in Hungarian), statistics
B. 4404. The angles of a polygon A1A2...A2n are all equal, and its sides satisfy A1A2=A3A4=...=A2n-1A2n and A2A3=A4A5=...=A2nA1. Prove that the polygon is cyclic.
(3 pont)
solution (in Hungarian), statistics
B. 4405. a and b are non-negative numbers such that a3+b3=2ab. Does that imply a2+b2 1+ab?
1+ab?
(4 pont)
solution (in Hungarian), statistics
B. 4406. Lines e1 and e2 are perpendicular, and P is a point on one of their angle bisectors, different from the intersection. Lines f and g pass through P, and intersect the lines ei at points Fi and Gi, respectively. Determine the locus of the intersection of the lines F1G2 and F2G1.
(4 pont)
solution (in Hungarian), statistics
B. 4407. Let k be a positive integer. How many non-negative solutions does the equation have?
(4 pont)
solution (in Hungarian), statistics
B. 4408. In a triangle ABC, the lengths of sides AC and BC are fixed, and the angle at vertex C is variable. The midpoint of side AC is M, the midpoint of side BC is N, and the centre of the square drawn over the side AB on the outside is O. For what value of will the sum of the distances OM and ON be a maximum?
(4 pont)
solution (in Hungarian), statistics
B. 4409. Assume that n is a positive integer and 2n+1 is a prime. What may be the remainder of this prime when divided by 240?
(4 pont)
solution (in Hungarian), statistics
B. 4410. The teacher in the maths club had an at most nth-degree polynomial in mind. The students may ask the value of the polynomial at any point on the real axis they want. What is the minimum number of points they need, in order to be able to decide in all cases whether the function is even?
(5 pont)
solution (in Hungarian), statistics
B. 4411. The axes of two right circular cones are parallel, and their apex angles are different. Prove that their common points all lie on the surface of a sphere.
(5 pont)
 |
Problems with sign 'A'Deadline expired on January 10, 2012. |
A. 548. Prove that
holds for arbitrary real numbers .
(5 pont)
A. 549. The diagonals of a circumscribed quadrilateral ABCD meet at E. Show that the incenters of the triangles ABE, BCE, CDE and DAE lie on a circle.
(Proposed by: G. Holló, Budapest)
(5 pont)
A. 550. Is it true that every sufficiently large positive integer is the sum of a Fibonacci number and a prime number?
(5 pont)
Upload your solutions above.
