A KöMaL 2018. februári fizika feladatai
Kérjük, ha még nem tetted meg, olvasd el a versenykiírást.
Feladat típusok elrejtése/megmutatása:
 |
M-jelű feladatokA beküldési határidő 2018. március 12-én LEJÁRT. |
M. 375. Mérjük meg egy ruhacsipesz szorítóerejét nyílásszögének függvényében!
Közli: Légrádi Imre, Sopron
(6 pont)
 |
G-jelű feladatokA beküldési határidő 2018. március 12-én LEJÁRT. |
G. 625. A toronyóra 1,5 m hosszú nagymutatóján az óra középpontjától a mutató vége felé mászik egy pók egyenletesen, 1 mm/s sebességgel. A pók pontban 12 órakor indul.
\(\displaystyle a)\) Mennyit mutat az óra, amikor a pók a mutató végére ér?
A mutató végére érve a pók a maga által szőtt fonálon ereszkedik le, melynek az egyik végét a mutató végéhez rögzíti.
\(\displaystyle b)\) Milyen sebességgel szője a fonalat, hogy 13 órakor éppen az indulási helyén legyen?
\(\displaystyle c)\) Milyen messze volt a pók az óra tengelyétől háromnegyed egykor?
(3 pont)
G. 626. Mennyi annak az \(\displaystyle \ell\) hosszúságú fonálingának a lengésideje (kis kitérések esetén), amelynek fonala középen egy szögbe ütközik, miközben áthalad az inga egyensúlyi helyzetén?
(3 pont)
G. 627. A Föld felszíne felett milyen magasságban lesz egy testre ható gravitációs vonzóerő éppen ugyanakkora, mint a Hold felszínén?
(3 pont)
G. 628. Reggelente mindig ugyanabban az órában megfigyelhetjük, hogy a Vénusz egyre közelebb kerül a Naphoz.
Vajon a Nap ,,előtt'' vagy pedig a Nap ,,mögött'' fog a Vénusz elhaladni?
Közli: Részegh Anna, Vácduka
(4 pont)
 |
P-jelű feladatokA beküldési határidő 2018. március 12-én LEJÁRT. |
P. 5001. Reggelente mindig ugyanabban az órában megfigyelhetjük, hogy a Vénusz egyre közelebb kerül a Naphoz.
Vajon a Nap ,,előtt'' vagy pedig a Nap ,,mögött'' fog a Vénusz elhaladni?
Közli: Részegh Anna, Vácduka
(4 pont)
P. 5002. A Föld középpontja enyhén hullámos ellipszispályán kering a Nap körül.
\(\displaystyle a)\) Mi az oka ennek a hullámosságnak?
\(\displaystyle b)\) Közelítőleg mekkora egy ilyen hullám amplitúdója?
Közli: Radnai Gyula, Budapest
(4 pont)
P. 5003. Két \(\displaystyle \ell\) hosszúságú fonálinga közvetlenül egymás mögött, egymással párhuzamos síkokban lenghet. Árnyékuk merőlegesen egy falra vetődik, időnként áthalad egymáson. Mindkét ingát ugyanakkora (kicsiny) szögben kitérítjük, majd \(\displaystyle t_0\) időkülönbséggel elengedjük. (\(\displaystyle t_0\) kisebb, mint az ingák lengésideje.)
\(\displaystyle a)\) Mikor találkozik az árnyékuk először?
\(\displaystyle b)\) Mikor következik be az \(\displaystyle n\)-edik találkozás?
Közli: Wiedemann László, Budapest
(4 pont)
P. 5004. Egy 8 méter hosszú, hajlékony fonál két végpontját azonos magasságban, egymástól 4 méter távolságban rögzítjük. A fonálon, arra felfűzve súrlódás nélkül mozoghat egy 0,5 kg tömegű test. A fonalat feszesen tartva a testet kezdősebesség nélkül úgy indítjuk el, hogy az indítási pont és a felfüggesztési pontok egy egyenesbe esnek.
Mekkora erő feszíti a fonalat, amikor a test a legnagyobb sebességgel halad?
Közli: Simon Péter, Pécs
(5 pont)
P. 5005. Két egyforma, henger alakú, bontatlan üdítőitalos doboz egyikét a mélyhűtőben megfagyasztjuk. Ezután egyszerre, egymás mellől indítjuk el őket egy lejtőn.
Melyik ér le hamarabb?
Példatári feladat
(3 pont)
P. 5006. Egy 200 g tömegű strandlabdát függőlegesen lefelé erősen a talajra dobunk. A labda a legjobban benyomott állapotában egy 10 cm átmérőjű körlap mentén érintkezik a talajjal, és ekkor a labdában lévő levegő nyomása 110 kPa lesz.
\(\displaystyle a)\) Mekkora a labda tömegközéppontjának legnagyobb gyorsulása, ha a talaj száraz és egy kicsit göröngyös?
\(\displaystyle b)\) Más értéket kapnánk-e a gyorsulásra, ha a talaj sima és nedves volna, és emiatt a labda talajjal érintkező része alatt nem maradna levegő?
(A külső légnyomás 100 kPa.)
Közli: Gnädig Péter, Vácduka
(5 pont)
P. 5007. Egy \(\displaystyle 70^\circ\)-os törőszögű prizmára lézersugarat bocsátunk. A sugár beesési szöge megegyezik a kilépési szöggel. A lézersugár az eredeti irányától \(\displaystyle 50^\circ\)-kal térül el.
Mekkora a prizma anyagának törésmutatója?
Közli: Zsigri Ferenc, Budapest
(3 pont)
P. 5008. Egy egyatomos gázt oly módon melegítünk, hogy a folyamat során a mólhője a gázállandó \(\displaystyle (R)\) legyen. Hányszorosára változik a gáz térfogata, ha a hőmérséklete a kétszeresére nő?
Példatári feladat
(5 pont)
P. 5009. Vákuumban \(\displaystyle B=2\) T indukciójú homogén, vízszintes irányú mágneses térben \(\displaystyle \ell=0{,}8\) m hosszú, igen vékony fonalú ingát a \(\displaystyle \boldsymbol B\)-re merőleges síkban vízszintesen kitérítünk, majd kezdősebesség nélkül elengedünk az ábra szerint.
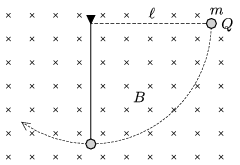
\(\displaystyle a)\) Mekkora töltést kell adnunk az inga \(\displaystyle m=0{,}1\) g tömegű gömbjének, hogy a legalsó ponton áthaladva a fonálerő a mágneses tér nélküli értékének 99%-a legyen?
\(\displaystyle b)\) Mekkora az egymás utáni két áthaladáskor mérhető fonálerők aránya?
Közli: Holics László, Budapest
(4 pont)
P. 5010. Egy ciklotronban protonok felgyorsításához 10 MHz frekvenciájú gyorsítófeszültségre van szükség. Mekkora frekvencia kell a deuteronok, az egyszeresen ionizált héliumatomok, illetve a kétszeresen ionizált héliumatomok felgyorsításához?
Példatári feladat nyomán
(4 pont)
P. 5011. A fémhúros gitár két legvékonyabb húrja az E és a H nagy szakítószilárdságú acélhuzal. A vékonyabb E húrt túlfeszítjük addig, amíg a G hangmagasságot elérve (egy egész hangközzel a 440 Hz-es normál A alatt) elszakad.
\(\displaystyle a)\) Milyen hangnál szakad el a H húr, ha azt is túlfeszítjük, és ugyanakkora szakítószilárdságú acélból készült?
\(\displaystyle b)\) Mekkora volt az E húr anyagának szakítószilárdsága?
\(\displaystyle c)\) A régóta használt húrok általában az alátámasztásnál vagy a hangolókulcsnál szakadnak el. Miért?
\(\displaystyle d)\) Miből lehetne még hangszerhúrt készíteni? Keressünk megfelelő anyagot a Függvénytáblázatban és az Interneten!
A gitárhúr rezgő részének hossza (menzúrahossz) 64 cm. Az acélhúr anyagának sűrűsége \(\displaystyle 7{,}8 \cdot 10^3~\rm kg/m^3\).
Közli: Vladár Károly, Kiskunhalas
(6 pont)
A fizika gyakorlatok és feladatok megoldásait honlapunkon keresztül küldheted be:
- megszerkesztheted vagy feltöltheted az Elektronikus munkafüzetben.
(Az interneten keresztül történő beküldésről olvasd el tájékoztatónkat)

