|
| [1315] rizsesz | 2006-08-21 15:27:37 |
 hát, a kecske által lelegelt terült egy körszelet kétszerese. innen pedig nem mehet nehezen.
|
|
| [1314] Vini | 2006-08-21 15:00:37 |
 Sziasztok.
Egy érdekes feladattal találkoztam. Így szól: Egy egység sugarú kör kerületén leverünk egy cölöpöt és kikötünk hozzá egy kecskét. Mekkora legyen a kötél amivel a kecskét kikötöttük, ha azt szeretnénk, hogy az egység sugarú kör területének felét tudja csak lelegelni.
Ha valaki meg tudná oldani, az jó lenne, mert én nem boldogulok vele. Meg lehet ezt egyáltalán középiskolás tudással oldani? Kösz
|
|
|
|
|
| [1310] jonas | 2006-08-01 01:26:54 |
 Még novemberben feladtam egy feladatot, amit senki nem oldott meg. Akkor ígértem két másik feladatot is, de ezeket nem tűztem ki érdeklődés hiányában, meg azért is, mert esetleg valaki bemondja, hogy szabad a gazda, és akkor szenvedhetek a megoldás leírásával. Mindhárom feladat arról a szemináriumról való, amelyre részben én gyűjtöttem a feladatokat.
Mivel most más okból leírtam ezek közül a második feladat megoldását, ezért ezt a feladatot most már nyugodtan feladhatom.
238. Az n-edik Catalan-szám 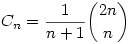 . Ismert, hogy ez egyenlő azon lépcsős utak számával, amelyek a kockás papírra rajzolt n jobbra mutató és n felfele mutató kis nyílból áll (valamilyen sorrendben), és nem megy a végpontokat összekötő átló fölé, vagyis minden prefixében legalább annyi jobbra nyíl van, mint fölfele mutató nyíl. . Ismert, hogy ez egyenlő azon lépcsős utak számával, amelyek a kockás papírra rajzolt n jobbra mutató és n felfele mutató kis nyílból áll (valamilyen sorrendben), és nem megy a végpontokat összekötő átló fölé, vagyis minden prefixében legalább annyi jobbra nyíl van, mint fölfele mutató nyíl.
Ezt tudva lássuk be, hogy bármely n-re
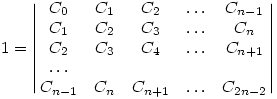
Ez a determináns a Catalan-sorozatból képzett Hankel-determináns, amelynek minden mellékátlójában egyenlő elemek állnak.
Lássuk be azt is, hogy
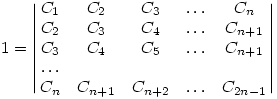
Ha valaki nem boldogul, akkor a megoldás itt olvasható (angolul).
Az első feladat tehát az (1141) hozzászólásban olvasható, a harmadikat viszont csak ennek a megoldása után szeretném föladni, mert összefügg.
|
| Előzmény: [1140] jonas, 2005-11-28 19:42:12 |
|
|
| [1308] 2501 | 2006-07-16 17:38:38 |
 Ez a kérdés a "Nehezebb matematikai problémák" témában is szerepel, a [296]-os hozzászólásban, de akkor addig gondolkoztam rajta, hogy végül teljesen elfelejtettem. :)
Bármely n hosszú dobássorozatot leírhatunk egy pozitív egészekből álló h1,h2,...,hm sorozatként, ahol hi az i-edik "egyszínű"-részsorozat hossza (tehát h1+h2+...+hm = n és m n). (Minden ilyen összeg valójában két sorozatot ír le, mivel a "színek" megcserélésével a leírás nem változik.) Nevezzük ezeket a sorozatokat n felbontásainak! n). (Minden ilyen összeg valójában két sorozatot ír le, mivel a "színek" megcserélésével a leírás nem változik.) Nevezzük ezeket a sorozatokat n felbontásainak!
Ebből a nézőpontból a kérdés úgy hangzik, hogy n-nek hány felbontása létezik, és ezek közül hányban szerepel k-nál nemkisebb tag (az eredeti kérdésre a válasz ezek aránya lesz). Ez utóbbit úgy is megkaphatjuk, hogy azokat számoljuk össze, amelyekben csak k-nál kisebb tagok szerepelnek, majd ezt az összesből kivonjuk.
Vezessük be az
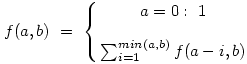
függvényt, amely azt adja meg, hogy a-nak hány olyan felbontása van, amely b-nél nemnagyobb pozitív egészekből áll.
(A fenti definíció azt "mondja", hogy f(a,b) értéke 1, hogyha a = 0. Egyébként pedig úgy kapjuk meg, hogy a-ból "lecsípünk" 1-et, 2-t, ... b-t (egészen addig, amíg a el nem fogy), minden esetben megnézzük, hogy a maradéknak hányféle felbontása van, és ezeket összegezzük.
Úgy emlékszem, hogy valamelyik IOI/CEOI válogatóversenyen volt egy feladat, amely valahogy úgy hangzott, hogy "Hányféleképpen lehet felugrálni egy a fokú lépcsőn, ha legfeljebb b fokot tudunk egyszerre átugrani?", és ez volt a megoldás.)
Ezzel kifejezve az eredeti kérdésre a válasz: 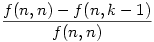
Az "érmés" vonatkozásban szemlélve az f(n,n) kifejezést láthatjuk, hogy egyenlő 2n-1-nel.
|
| Előzmény: [1303] Virág, 2006-07-16 11:29:29 |
|
| [1307] Virág | 2006-07-16 16:20:33 |
 Időközben megnéztem a F1-et, de érintőlegesen a feladaton is gondolkodtam.... :o) Nekem nagyon bonyolult, lehet, hogy nincs is erre konkrét képlet?
|
| Előzmény: [1306] Sirpi, 2006-07-16 13:51:49 |
|
| [1306] Sirpi | 2006-07-16 13:51:49 |
 Mondjuk ez a képlet tuti nem jó. Ha k=1, az azt jelenti, hogy legalább egy hosszú egyformákból álló blokk van, ennek esélye 1, nem pedig n/2n-1. Ugyanúgy ha k=2, akkor az esély 1-1/2n-1, nem pedig a képletből adódó (n-2)/2n-1. Jó kérdés, hogy mi lehet a helyes képlet...
|
| Előzmény: [1305] Virág, 2006-07-16 12:15:46 |
|
|
| [1304] Sirpi | 2006-07-16 12:09:14 |
 Na, csak hogy rendesen meglegyen (még nem gondoltam bele, hogy jó-e a képlet, és eltartott vagy 2 percig, míg rájöttem, mi akar az ott lenni...). Tehát annak esélye, hogy lesz legalább k db. egyforma oldal n dobásból:
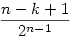
ami n=k-ra 1/2n-1-et ad (legalább ez a része tuti jó :-) ).
|
| Előzmény: [1303] Virág, 2006-07-16 11:29:29 |
|
| [1303] Virág | 2006-07-16 11:29:29 |
 Sziasztok! Egy érdekes feladat, legalábbis nekem. Tudnátok segíteni? Egy pénzérmét feldobok "n"-szer. Mi a valószínűsége annak, hogy lesz legalább "k" darab egyforma dobás egymás után? (Tehát "k" darab fej, vagy "k" darab írás közvetlenül egymás után.)
Valaki szerint ez a képlet talán jó?
2*(n-k+1)/(2 n) Ha n=k, akkor lesz: 1/(2(k-1)) , ajaj nem tudok beírni egy jelet, de gondolom tudjátok.
|
|
|
|
| [1300] Suhanc | 2006-07-11 10:16:01 |
 Kedves Mindenki!
Vérszemet kapva, a 236.feladat után szabadon:
237.Feladat Legyenek x, y, z, pozitív valós számok! Igazoljuk, hogy ekkor:
a) 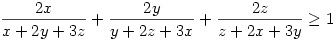
b) 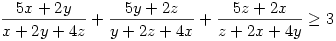
|
|
| [1299] jonas | 2006-07-07 13:01:35 |
 A javított kód -- ha valakit még érdekel ezek után:
Ky8qLi8iMV0yPDovXCIxKDYkMTApIzoxZTV9LmkuMWU2CisvKi4vIjFdMjwv
XCIxKDYkMTApIzoxZTV9LmkuMWU2Cg==
|
| Előzmény: [1284] jonas, 2006-06-21 12:24:22 |
|
|
| [1297] lorantfy | 2006-07-05 23:23:32 |
 Szia Suhanc!
Kösz a megoldást! Valóban az ismétlés nélküli és az ismétléses kombináció tipikus esetei ezek a példák, csak erre nem olyan könnyű rájönni.
Még a 233. feladat maradt állva, de Sirpi [1289] segítségével remélem erre is vállalkozik valaki!
|
| Előzmény: [1296] Suhanc, 2006-07-05 22:33:44 |
|
| [1296] Suhanc | 2006-07-05 22:33:44 |
 Kedves László!
Ha nem olvastam figyelmetlenül a hozzászólásokat, a 234.feladat még él. Egy lehetséges megoldás:
a)Tegyük fel, hogy valaki odaad nekünk 6 különböző számjegyet, azzal a kéréssel, csináljunk belőle az a)-nak megfelelő hatjegyű számot. Ekkor a legkisebb számjegyet írjuk előre, utána a második legkisebbet... azaz, e 6 számjegyből pontosan egy, a feladat feltételeinek megfelelő szám készíthető. Azt kell még eldöntenünk, hány ilyen számjegyhatos választható ki. A számjegyeknek a szigorú monotonitás miatt kell különbözőeknek lenniük, és 0 nem szerepelhet közöttük, hiszen azt csak a legelső helyre írhatnánk, de 0-val nem kezdünk számot. Így 9 számjegyből kell 6 különbözőt kiválasztanunk. Ez 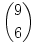 féleképp tehető meg. féleképp tehető meg.
b) A feladat az a)-hoz hasonló, de itt "csak" monotonitás az elvárt, így azonos számjegyek is lehetnek, ám 0 itt sem. Tehát itt 9 számjegyből ismétléssel kell kiválasztanunk 6-ot. Az ismert módon ez 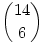 féleképp tehető meg. féleképp tehető meg.
|
| Előzmény: [1283] lorantfy, 2006-06-21 09:41:24 |
|
| [1295] Suhanc | 2006-07-05 19:47:19 |
 Kedves Tibi!
Egy lehetséges megoldás a feladatodra:
Írjuk az egyenlőtlenség jobb oldalán az 1-ek helyére a+b+c+d-t:
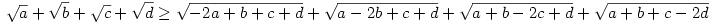
Legyen most
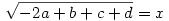
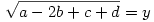
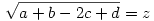
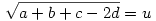
Ekkor:
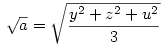
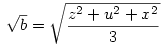
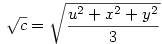
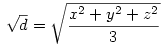
A bizonyítandó egyenlőtlenség ekkor:
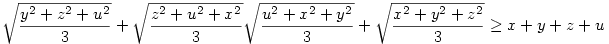
Nyilvánvaló, hogy x,y,z,u  0 . A bal oldalon a tagokat négyzetes-számtani közepekel becsülve épp a bizonyítandó állítást kapjuk. 0 . A bal oldalon a tagokat négyzetes-számtani közepekel becsülve épp a bizonyítandó állítást kapjuk.
Egyenlőség x=y=z=u esetén lehetséges, melyből a=b=c=d szükséges és elégséges feltétel levezethető.
|
| Előzmény: [1294] lorytibi, 2006-07-04 20:18:29 |
|
| [1294] lorytibi | 2006-07-04 20:18:29 |
 Sziasztok!
Matektáborban voltam a múlt héten és van egy példa, amit nem tudtunk megoldani:
236. feladat: Bbh., ha ![a,b,c,d \in \Big[0;\frac13 \Big]](keplet.cgi?k=D04D688A33348BD6) és a+b+c+d=1, akkor és a+b+c+d=1, akkor
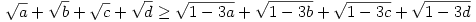
|
|
|
| [1292] lorytibi | 2006-06-24 16:50:54 |
 235.feladat megoldása: Egy konvex kilencszögnek 27 átlója van. Mivel nincs két párhuzamos átló, ezért ha az átlókat az egyik metszéspontba toljuk, akkor 54 félegyenes indul ki a pontból, 54 szöget alkotva. Így a szögek átlaga 360°/54, ami biztosan kisebb 7°, tehát biztosan van két olyan átló, melyek egyenesei 7°-nál kisebb szöget zárnak be.
|
| Előzmény: [1291] nadorp, 2006-06-23 08:34:47 |
|







 n). (Minden ilyen összeg valójában két sorozatot ír le, mivel a "színek" megcserélésével a leírás nem változik.) Nevezzük ezeket a sorozatokat n felbontásainak!
n). (Minden ilyen összeg valójában két sorozatot ír le, mivel a "színek" megcserélésével a leírás nem változik.) Nevezzük ezeket a sorozatokat n felbontásainak!  2a
2a

