| [1673] S.Ákos | 2007-01-01 19:11:48 |
 Maradékvizsgálat nélkül: Mivel a 0001;0002;0004;0008;0016 végződések nem felelnek meg, így az utolsó négy számjegyből alkotott szám osztható 16-tal és 1111-gyel, de ezeknek a közös többszörösei 0;17776;... így csak a 0000 jöhet szóba, de ez lehetetlen.
|
| Előzmény: [1671] jonas, 2007-01-01 17:32:26 |
|
|
| [1671] jonas | 2007-01-01 17:32:26 |
 (a) 239=549755813888
(b) Ehhez elég a 2-hatványok 10000-es maradékát megvizsgálni. Ez persze ciklikus, hiszen 2504 24 24 16mod 10000. A maradékok 2503-ig sorban könnyen kiszámolhatóak (nem másolom ide az összeset): 16mod 10000. A maradékok 2503-ig sorban könnyen kiszámolhatóak (nem másolom ide az összeset):
0001 0002 0004 0008 0016 0032 0064 0128 0256 0512 1024 2048 4096 8192 6384 2768 5536 1072 2144 4288 8576 7152 4304 8608 7216 4432 8864 7728 ... 8752 7504 5008
Ezek között pedig nincs 1111-gyel osztható.
|
| Előzmény: [1666] Python, 2007-01-01 15:29:09 |
|
|
| [1669] Lóczi Lajos | 2007-01-01 17:21:13 |
 a.) Az első 1600 kitevő átvizsgálása az alábbi eredményt adja: 2n pontosan akkor végződik 3 egyforma számjegyre, ha n az alábbi:
n=39,139,239,339,439,.... Ekkor amúgy mindig 888-ra végződik 2n.
b.) A számítógép 85 másodperc gondolkodás után nem tudott olyan 2-hatványt mondani, ami 4 egyforma számjegyre végződne. Az átvizsgált n kitevők tartománya: n=1-től egészen n=107-ig.
|
| Előzmény: [1666] Python, 2007-01-01 15:29:09 |
|
|
|
| [1666] Python | 2007-01-01 15:29:09 |
 304. feladat
a)Végződhet-e egy kettőhatvány 3 egyforma számjegyre? (10-es számrendszer)
b)Végződhet-e egy kettőhatvány 4 egyforma számjegyre? (10-es számrendszer)
|
|
| [1665] Lóczi Lajos | 2006-12-31 14:00:09 |
 Számunkra már több, mint egy éve nyitott az alábbi ártatlannak tűnő kérdés: oldjuk meg a valós számok halmazán a
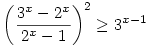
egyenlőtlenséget. Az eredményt persze tudjuk, csak a bizonyítást nem. Hátha valaki talál egy ügyes utat...
|
|
|
|
| [1662] Cckek | 2006-12-30 17:53:39 |
 Jólismert egyenlőtlenségek a G<L<A ahol
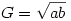 , ,
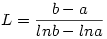 , ,
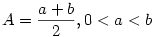 . .
Tud rájuk valaki egy egyszerű bizonyítást?
|
|
| [1661] HoA | 2006-12-29 16:40:53 |
 A képlet bizonyítása: Rakjunk le egy sorba s + n - 1 ( 222 + 4 - 1 = 225 ) fehér korongot. Közülük n-1 (3) tetszőlegeset takarjunk le egy-egy fekete koronggal. Minden ilyen lefedés a le nem takart s (222) korongot n (4) csoportra bontja, melyek közt 0 elemszámúak is lehetnek. Feleltessük meg, mondjuk balról jobbra az egyes csoportok elemszámát az ai (x,y,z,t) változóknak, ekkor egyenletünk egy megoldását kapjuk. Így kölcsönösen egyértelmű leképezést kapunk a lefedések és a megoldások között, tehát megoldás is ponosan annyi van, mint lefedés. Ezek száma pedig a képlet szerinti.
|
| Előzmény: [1660] Cckek, 2006-12-29 10:33:28 |
|
|
|
|
| [1657] Cckek | 2006-12-28 15:06:49 |
 Hány megoldása van a természetes számok halmazában az x+y+z+t=222 egyenletnek?
|
|
| [1656] HoA | 2006-12-27 13:24:26 |
 Mivel eddig senki sem szólt hozzá, leírok egy megoldást.
Racionáls a,b 0 -ra x pontosan akkor racionális, ha w=x/a , és y pontosan akkor, ha z=y/b is az. x=wa-t és y=zb-t helyettesítve w2+z2=1 adódik. Legyen 0 -ra x pontosan akkor racionális, ha w=x/a , és y pontosan akkor, ha z=y/b is az. x=wa-t és y=zb-t helyettesítve w2+z2=1 adódik. Legyen 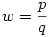 , , 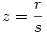 , ahol p,q,r,s egészek. , ahol p,q,r,s egészek. 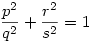 ; p2s2+r2q2=q2s2 Legyen q és s legnagyobb közös osztója n, q=tn, s=un, ahol t és u relatív prímek. ; p2s2+r2q2=q2s2 Legyen q és s legnagyobb közös osztója n, q=tn, s=un, ahol t és u relatív prímek.
p2u2n2+r2t2n2=t2u2n4 ; p2u2+r2t2=t2u2n2 A baloldalon t és u relatív prím volta miatt p2 osztható t2 -tel és r2 osztható u2 -tel. Legyen p=kt, r=mu. k2t2u2+m2u2t2=t2u2n2
k2+m2=n2
Vagyis tetszőleges k,m,n pithagoraszi számhármashoz kapunk megoldást. Visszafelé haladva tetszőleges relatív prím t-t és u-t véve 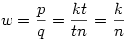 , , 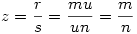 , , 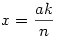 , , 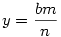
Az ellipszis racionális koordinátájú pontjai tehát a 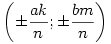 pontnégyesek, ahol a és b az ellipszis tengelyei, k,m,n pithagoraszi egészek, ahol a nemnulla hármasokon kívül 1;0;1 és 0;1;1 is megengedett. Könnyen belátható, hogy ha k,m,n primitív pithagoraszi számhármas, akkor minden pontot csak egyszer kapunk meg. pontnégyesek, ahol a és b az ellipszis tengelyei, k,m,n pithagoraszi egészek, ahol a nemnulla hármasokon kívül 1;0;1 és 0;1;1 is megengedett. Könnyen belátható, hogy ha k,m,n primitív pithagoraszi számhármas, akkor minden pontot csak egyszer kapunk meg.
|
| Előzmény: [1625] Cckek, 2006-12-15 14:58:40 |
|
|
|
| [1653] Hephon | 2006-12-25 16:17:19 |
 Minden üveg sorszáma elfér 10 számjegyen binárisan (<1024). Minden bináris helyiérték 1-1 halálraitélthez tartozik. Minden borral megitatja azokat az embereket, ahol ez a helyiérték 1, tehát az 1. borbol csak az első szolga, a 100. borbol(64+32+4) tehát a 3. 5. 6. halálraitéltek isznak. 30. nap után az összes halottbol kiszámítha, hogy melyik bor volt a mérgező.
|
| Előzmény: [1652] Cckek, 2006-12-25 15:55:58 |
|
| [1652] Cckek | 2006-12-25 15:55:58 |
 Kellemes ünnepeket mindenkinek. És... a következő kis feladatot: Egy császár 1000 üveg borából 1 mérgezett. A császár kiadja a nagyvezérnek a parancsot, 40 nap alatt állapítsa meg melyik üveg mérgezett. Ehez kap 10 halálraítéltet akikkel a borokat kostoltathatja. A méreg 30 nap mulva hat. Hogyan jár el a nagyvezér?
|
|
|
| [1650] Iván88 | 2006-12-21 20:34:16 |
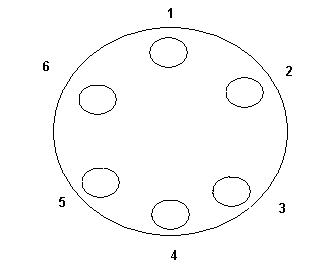
 Mivel a rendszer nem engedi feltölteni a 343 bájtos ábrámat (ami jóval a maximum alatt van) a kitöltetlen ábrádon fogok magyarázni. 4 különböző eset van a kézbedugásra:
3 szomszédos állásba (612)
2 szomszédos állásba, (124 ill. 614-ezek forgatással nyilván nem vihetők át egymásba)
0 szomszédos állásba (246)
Az össze további eset ezek közül valamelyiknek az elforgatottja.
A kapcsolók állása nyilván csak goldolatban van megszámozva, különben nem feladat. Ezzel a 4 félével, ha nincs szerencsénk, akkor kijöhet, hogy csak az 1246 kapcsolókhoz nyúlunk hozzá.
Tehát, ha a 3-as, és az 5-ös kapcsoló különböző állású, akkor elvileg az is előfordulhat, hogy sose nyúlunk hozzájun, és az ajtó is zárva maradhat az idők végezetéig.
Tehát áltaéános algoritmus nem létezik.
|
| Előzmény: [1649] magusocska, 2006-12-21 19:00:59 |
|
| [1649] magusocska | 2006-12-21 19:00:59 |
 Eddig jutottam:
Jelöljük a kapcsoló két állását 1-gyel és 2-vel!
Jelöljük a kapcsolókat 1-6, a felsőtől az óramutató járásával megegyezően.
[Ekkor az első kapcsoló jelölése legyen 1(1) vagy 1(2) attól függően, hogyan áll a kapcsoló 1 vagy 2 állásban, bizonytalan helyzetben 1 (1/2).]
Minden továbblépés előtt feltételezzük, hogy nem nyílik ki.
[Szerencsés esetben persze bármikor kinyílhat, akár induláskor is :*-) ]
1. Fogjunk meg három egymás melletti kapcsolót, és állítsuk mindhármat 2-re, ha nem az volt! [1(2),2(2),3(2) kapcsolóállás jön létre]
2.A pörgetés után fogjunk meg három nem egymás mellettit, és állítsuk 2-re, ha nem az volt!
A lehetséges esetek:
hely----Biztos--------------------bizonytalan
1,3,5--1(2),2(2),3(2),5(2)--------4(1/2),6(1/2)
2,4,6--1(2),2(2),3(2),4(2),6(2)---5(1/2)
Tehát két pörgetés után mindkét esetben legalább egy bizonytalan helyem van. Innentől én is bizonytalan vagyok.
Mivel a pörgetés véletlenszerű kezdőpontú felállásokat hoz, elvben bármeddig pörgethetek, nézhetem, hogy van-e átállítandó (ha 1 akkor átállítom), de mi garantálja, hogy a három kezem közül valamelyik alá kerül a hátralévő (1 vagy 2) a maradék 3 pörgés alatt?
Nem látom értelmét annak sem, hogy az 1,2,3 és a 2,4,6 után egy újabb lépésvariációt vezessek be (mondjuk 1,2,4).
Ötlet?
|
 |
| Előzmény: [1647] magusocska, 2006-12-21 10:52:17 |
|




 24
24




 0 -ra x pontosan akkor racionális, ha w=x/a , és y pontosan akkor, ha z=y/b is az. x=wa-t és y=zb-t helyettesítve w2+z2=1 adódik. Legyen
0 -ra x pontosan akkor racionális, ha w=x/a , és y pontosan akkor, ha z=y/b is az. x=wa-t és y=zb-t helyettesítve w2+z2=1 adódik. Legyen 


