 Köszönöm Sirpi!
A lenti számháromszög két utolsó sora a 12 és 13 esetét írja le, azok már nem fértek el egy sorba...
Értelemszerűen az előző sorok számainak összegei (felfelé haladva) 3 - nak 11, 10, 9,...1, 0 hatványai.
Ez emlékeztet a permutációk fixpontjaira! Az ismétléses variáció fixpontjaira van valahol irodalom?
A bal oldali oszlop:1 2 4 8 16...mint a permutációknál: a nulla fixpontok darabszámát jelentené. majd jobbra haladva az egy, kettő, stb fixpontok darabszámát!
Egyáltalán van ilyen fogalom? Ha van milyen néven keressem?
Mert ez, ha általánosítjuk, "m" alapú hatvánnyal leírható minden ismétléses variációra igaz!
m=3
1
2, 1
4, 4, 1
8, 12, 6, 1
16, 32, 24, 8, 1
32, 80, 80, 40, 10, 1
64, 192, 240, 160, 60, 12, 1
128, 448, 672, 560, 280, 84, 14, 1
512, 2304, 4608, 5376, 4032, 2016, 672, 144, 18, 1
1024, 5120, 11520, 15360, 13440, 8064, 3360, 960, 180, 20, 1
2048, 11264, 28160, 42240, 42240, 29568, 14784, 5280, 1320, 220, 22,1
4096, 24576, 67584, 112640, 126720, 101376, 59136, 25344, 7920, 1760, 264, 24, 1
8192, 53248, 159744, 292864, 366080, 329472, 219648, 109824, 41184, 11440, 2288, 312, 26, 1
lásuk m=4 esetén!
1
3, 1
9, 6, 1
27, 27, 9, 1
81, 108, 54, 12, 1
243, 405, 270, 90, 15, 1
729, 1458, 1215, 540, 135, 18, 1
2187, 5103, 5103, 2835, 945, 189, 21, 1
Maple kóddal:
** :a hatvány jele.
for i from 0 to 13 do seq(binomial(i, j)*3**(i-j), j = 0 .. i) od;#
3**(i-j) > itt a 3 egyenlő m=4 minusz egy, etc...
|







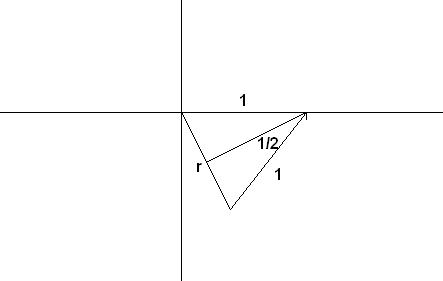



 -nak.
-nak.  esetén van nyerő stratégiája. Utóbbi esetben könnyű látni, hogy a nyuszival azonos sebességű farkasok esetén nem tud kijutni: a farkasok mindig a nyuszi oldalakra vett merőleges vetületébe mozdulnak (már kezdetben is ott vannak). A feladat többi részét egyelőre nem lőném le.
esetén van nyerő stratégiája. Utóbbi esetben könnyű látni, hogy a nyuszival azonos sebességű farkasok esetén nem tud kijutni: a farkasok mindig a nyuszi oldalakra vett merőleges vetületébe mozdulnak (már kezdetben is ott vannak). A feladat többi részét egyelőre nem lőném le.