| [2752] HoA | 2008-11-13 16:35:48 |
 Vagy nagyon nem értem amit írsz, vagy kicsit összekevered a dolgokat. Ha az a kérdés, melyik az a legkisebb, tizes számrendszerben felírt, csak 0 és 1 jegyekből álló szám, amelyik az adott számnak többszöröse, és ebben mennyi a számjegyek összege, akkor "1 (számjegyösszeg 1), 2-nek 10 (1)" rendben van. Ugyancsak jó a "4-nek 100 (1), 5-nek 10 (1)" , valamint "7-nek 1001 (2), 8-nak 1000 (1)". De mi az, hogy 3-nak 3 (3) ? Mióta áll a "3" csak egyesekből és nullákból? Vagy mi az, hogy 6-nak 12 (3) ? És 9-nek 9? Szerintem 3-nak 111 (3), 6-nak 1110 (3) és 9-nek 111111111 (9).
Ami az érdemi részét illeti, miért gondolod, hogy egy jó nagy prímszámnak a csak 0-1 jegyekből álló többszörösei között van olyan, amelyben csak 9 egyes szerepel?
|
| Előzmény: [2751] Sirpi, 2008-11-13 15:53:19 |
|
| [2751] Sirpi | 2008-11-13 15:53:19 |
 Ez a probléma tegnap merült fel bennem, úgyhogy ide be is írom (egyelőre még nem oldottam meg):
Az ugye közismert, hogy minden egész számnak van csupa 0-sból és 1-esből álló többszöröse. Hasonló minimalizmusra törekedve azt is meg lehet keresni, hogy az egyes számoknak melyik az a többszöröse, aminek számjegyösszege minimális: például az 1-nek a legkisebb ilyen többszöröse az 1 (számjegyösszeg 1), 2-nek 10 (1), 3-nak 3 (3), 4-nek 100 (1), 5-nek 10 (1), 6-nak 12 (3), 7-nek 1001 (2), 8-nak 1000 (1), 9-nek 9 (9) stb. Vagyis Ezt a sorozatot kapjuk: 1 1 3 1 1 3 2 1 9 1 2 3 ...
Na, akkor a kérdés: Igaz-e, hogy minden számnak van olyan többszöröse, ahol a számjegyösszeg legfeljebb 9? (a 9-cel osztható számok miatt ennél alacsonyabb korlát biztos nincs) Tovább megyek: ha ez igaz, és ha a 3-mal osztható számokat nem nézzük, akkor lehet vajon kisebb korlátot mondani?
Valamint általánosan is érdekelne a dolog: minden g számrendszerben igaz az, hogy minden számnak van olyan többszöröse, aminek (g-es számrendszerbeli) számjegyösszege legfeljebb g-1? És ha igen, akkor a g-1-hez relatív prím számoknál lejjebb lehet ezt a korlátot szorítani?
|
|
|
| [2749] Dorottya | 2008-11-11 19:44:44 |
 Tudnátok segíteni? Az O középpontú körvonalon az X, A, B és Y pontok úgy helyezkednek el, hogy az XOY szöget az OA és az OB félegyenesek három egyenlő részre osztják. Az XOA és az YOB szögek szögfelezői merőlegesek egymásra. Mekkora az XOY szög? Előre is köszönöm...
|
|
| [2748] Gyöngyő | 2008-11-10 22:39:32 |
 Ebben a könyvben rendesen le van irva! De tudok majánlani még egy könyvet,az egyik tanárom irta Németh József:Előadások a végtelen sorokról ami szintén polygonos!
|
| Előzmény: [2747] Mirinda, 2008-11-10 22:27:39 |
|
| [2747] Mirinda | 2008-11-10 22:27:39 |
 Ohh köszi szépen.És ööö ebbe a könyvbe le van vezetve,vagy részletesen ki van e tárgyalva?vagy csak néhány sornyi említés van róla.....köszi elöre is a válaszokat Üdv.:Dani
|
|
|
| [2745] Alma | 2008-11-09 22:25:45 |
 Szia,
régebben én is elgondolkodtam ezen a kérdésen (najó, rákerestem a neten :D). Akkor én magam is megtaláltam a Weierstrass függvényt, és be is bizonyítottam, hogy valóban folytonos, de sehol nem differenciálható (legalábbis valami bizonyítás szerű dolgot csináltam). Wikipédián keress rá, hogy "Weierstrass function", ott lesz egy cikk. Angol ez is, de magyarul szerintem kizárt, hogy találsz valami jót erről. Érdemes vizsgálni a függvényt (folytonosság szempontjából), és érdemes megpróbálni deriválni is szerintem. Régebben ábrázoltattam is, ezt most felteszem a netre: http://rapidshare.com/files/162238406/Weierstrass.bmp.html Bár a wikipédián is van ábrázolva.
üdv, Alma
|
| Előzmény: [2741] Mirinda, 2008-11-09 01:11:16 |
|
|
| [2743] Mirinda | 2008-11-09 19:35:00 |
 Köszi szépen.Csak sajna angol...magyarul sehol se találtam erröl a témáról.Lehet muszáj lesz nekiülnöm és forditani,de a tanárom azt mondta hogy nagyon nehéz,nemhogy még angolul.De azér thx még1szer,és ha valaki kicsit értene 1 picit ehez annak megköszönném nagyon...fontos..:S
|
|
|
| [2741] Mirinda | 2008-11-09 01:11:16 |
 helo mindenkinek!Egy olyan kérdéssel fordulnék hozzátok hogy:Mondjunk egy olyan függvényt amely mindenhol folytonos és sehol sem deriválható!!! 1-2 link-nek is örülnék a feladattal kapcsolatban,de örömmel várom a válaszokat is. Köszönöm előre is !!! Üdv.: Mirinda
|
|
| [2740] Ali | 2008-11-06 10:03:16 |
 Szervusz, csak egy megoldása van, az amit írtál.
Biz: t=z helyettesítéssel kapjuk, hogy (x-z)[(f(x)+g(x)-2z] 0. Ha x > z, akkor f(x)+g(x) 0. Ha x > z, akkor f(x)+g(x) 2z 2z  f(x)+g(x)-2x f(x)+g(x)-2x 2(z-x). Ha x<z, akkor f(x)+g(x) 2(z-x). Ha x<z, akkor f(x)+g(x) 2z 2z  f(x)+g(x)-2x f(x)+g(x)-2x 2(z-x). Vagyis |f(x)+g(x)-2x| 2(z-x). Vagyis |f(x)+g(x)-2x| 2|z-x|. Ez teljesül 2|z-x|. Ez teljesül  z z U -ra, ezért f(x)+g(x)=2x. U -ra, ezért f(x)+g(x)=2x.
Elvégezve a g(x)=2x-f(x) helyettesítést az eredeti egyenlőtlenségben, némi átalakítás után kapjuk, hogy [2x-f(x)](z-t)+(x-z)2+(x-t)2 0. t=x helyettesítés után (z-x)[z+x-f(x)] 0. t=x helyettesítés után (z-x)[z+x-f(x)] 0 kell hogy teljesüljön 0 kell hogy teljesüljön  z z U -ra. U -ra.
Ha z>x, akkor f(x) z+x z+x  f(x)-2x f(x)-2x z-x. Ha z<x, akkor f(x) z-x. Ha z<x, akkor f(x) z+x z+x  f(x)-2x f(x)-2x z-x z-x  |f(x)-2x| |f(x)-2x| |z-x| igaz |z-x| igaz  z z U -ra. Ebből már következik, hogy f(x)=2x. U -ra. Ebből már következik, hogy f(x)=2x.
Honnan jött ez a feladat ?
|
| Előzmény: [2739] Cckek, 2008-11-05 18:53:37 |
|
|
| [2738] Lóczi Lajos | 2008-10-22 14:44:09 |
 Adjuk meg az összes olyan c valós számot, amelyre az x4-2x2-3x+c polinomnak pontosan két valós gyöke van.
|
|
|
| [2736] jenei.attila | 2008-10-16 12:49:00 |
 A valós számokhoz fogok megadni temészetes számokból álló sorozatokat a következőképpen: legyen x egy valós szám, és tekintsük az x-nél kisebb racionális számok X halmazát (ha jól emlékszek, Dedekind szeletnek nevezik). Mivel a rac. számok halmaza megszámlálható, ezért sorozatba rendezhető. Feleltessük meg X-nek (és ezzel együtt x-nek) azt a természetes számokból álló sorozatot, amely a most említett racionális számok sorbarendezése szerint az X-beli racionális számok indexeit tartalmazza. Ez a természetes számoknak egy részhalmaza lesz, jelöljük Nx-szel. Ha x és y valós számokra x<y, akkor a megfelelő Dedekind szeleteikre X Y, ezért Nx Y, ezért Nx Ny is igaz. Minden x valós számhoz megadva a szóban forgó Nx-et, a természetes számok részhalmazainak egy olyan rendszerét kapjuk, amelyben bármely két elem összehasonlítható (a tartalmazásra nézve), hiszen bármely két valós szám is összehasonlítható (a szokásos rendezési relációra nézve).Másrészt ez a rendszer nem megszámlálható, mint ahogy a valós számok halmaza sem az. Ny is igaz. Minden x valós számhoz megadva a szóban forgó Nx-et, a természetes számok részhalmazainak egy olyan rendszerét kapjuk, amelyben bármely két elem összehasonlítható (a tartalmazásra nézve), hiszen bármely két valós szám is összehasonlítható (a szokásos rendezési relációra nézve).Másrészt ez a rendszer nem megszámlálható, mint ahogy a valós számok halmaza sem az.
|
| Előzmény: [2733] Csimby, 2008-09-25 16:56:11 |
|
| [2735] sakkmath | 2008-10-07 12:46:46 |
 Szia!
A Mathematics Magazine 2008/júniusi számának NET-re tévedt változatában is olvasható ez a feladat. Javasolom, hogy csak az általuk megadott beküldési határidő után, azaz 2008. november 2-től tegye közzé bárki az ott 1797-es sorszámú feladat megoldását.
|
| Előzmény: [2727] Gyöngyő, 2008-09-10 17:31:24 |
|
| [2734] kiskiváncsi | 2008-09-26 00:11:56 |
 1369 et nézegettem. Epsilon 1374 ebből jön, továbbá egy jó rekurzió amiből az indukciós feltevés (1376 kérdés) és egy jó Gamma fv a kifejezésre. De számoljatok utána. Epsilon :)
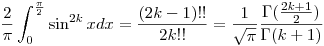
ez k>-1/2 re igaz, de csak 2k (páros) kitevőre
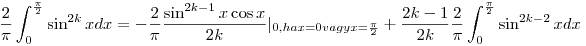
ez k>0 ra igaz
vagyis a bizonyitando
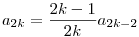
igaz
akkor
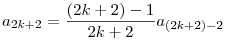 is igaz is igaz
|
|
|
|
|
|
|
|










 0. Ha x > z, akkor f(x)+g(x)
0. Ha x > z, akkor f(x)+g(x) f(x)+g(x)-2x
f(x)+g(x)-2x 2z
2z  z
z U -ra, ezért f(x)+g(x)=2x.
U -ra, ezért f(x)+g(x)=2x. 

 Y, ezért Nx
Y, ezért Nx
 ,t,Re(s)>0 továbbá x független t, s és
,t,Re(s)>0 továbbá x független t, s és