| [2802] leni536 | 2008-12-28 15:10:48 |
 Egyetértek, az ábra és a magyarázat nem egyeztethető össze. Az eredeti publikációjában található kép alapján is a B és D pontok környékén lesz a keresett különbség.

Forrás
Viszont nem értem, hogyan kerül ez az érdekes matekfeladatokhoz :P
|
| Előzmény: [2801] lorantfy, 2008-12-28 11:44:00 |
|
| [2801] lorantfy | 2008-12-28 11:44:00 |
 Sziasztok!
A Römer-féle fénysebesség mérés elvéről van szó. Nézzétek meg a linkeket. Szerintem ez a magyarázat hibás! Éppen a B és D pontok környékén lesz különbség a hold eltűnési idejében. Sulinet és Corvus
|
|
|
| [2799] Csimby | 2008-12-17 01:15:34 |
 338.feladat Legyen G egy p-reguláris párosgráf, melynek mindkét osztályában p2+p+1 csúcs van, és nem tartalmaz 4 hosszú kört. Igaz-e, hogy bármely két egy osztályba tartozó csúcsnak pontosan 1 közös szomszédja van?
|
|
|
| [2797] jenei.attila | 2008-12-15 18:50:13 |
 Nem ismertem ezt a linket, sőt a feladatot is csak nemrég hallottam. Majd elolvasom, de azt javaslom a fórumtársaknak, hogy próbálják meg maguk megoldani. Nekem sikerült, nem is volt olyan nehéz, de nagyon jó kis tanulságos feladat ez. Állítólag még réges-régen egy spec. mat. szakos osztályban félévi ötös járt a megoldásáért.
|
| Előzmény: [2796] Lóczi Lajos, 2008-12-15 18:21:51 |
|
|
| [2795] jenei.attila | 2008-12-15 11:07:58 |
 Előállítható-e a valós számokon értelmezett f(x)=x identitás fv. két periodikus fv. összegeként?
|
|
|
| [2793] sakkmath | 2008-12-14 13:34:37 |
 Szia zsizsike! A jelöléseid számomra kibogozhatatlanok, hiányosak. Nem tudok rájönni, hogy mi a konkrét feladat. Kattints a bal oldal TeX tanfolyam gombjára, tanulmányozd a TeX minitanfolyamot és írd be helyesen a feladatot. A másik lehetőség arra az esetre, ha elektromos formátumban, pl. WORD/MathType-egyenletszerkesztővel már hibátlanul leírtad a feladatot: ekkor egy képkezelő program képernyőlopó funkciójával ("Capture screen", ha pl. XnView-et használsz) .gif-, vagy .jpg-képet készíthesz a példáról és felteheted (Ábra feltöltés). Üdv: sakkmath
|
| Előzmény: [2792] zsizsike, 2008-12-14 10:59:21 |
|
| [2792] zsizsike | 2008-12-14 10:59:21 |
 sziasztok! van egy érdekes feladat előttem, de sehogy nem jövök rá, hogy hogyan lesz az eredmény annyi, amennyi le van írva megoldásként. Íme: lim/a gyök x -gyök a/x -a . Nos nem tudom, ebből hogyan lesz lim/a 1/gyök x + gyök a? Ha valaki tudja a választ, pontosabban a levezetést, akkor , kérem, segítsen. honnan kerül oda az 1, mert azt értem, hogy a reciprokkal szorzok, de innen hogy lesz az osztó 1?? lehet hogy még korán van? SOS!
|
|
|
| [2790] psbalint | 2008-12-13 16:07:07 |
 337. feladat (remélem még nem volt, én nem tudtam megcsinálni) Mennyi maradékot ad 1980-nal osztva az 123456789101112...19781979 szám?
|
|
| [2789] Cogito | 2008-12-12 19:30:50 |
 336. feladat. Legyen t 0, x, y, z pedig pozitív szám. Bizonyítsuk be, hogy 0, x, y, z pedig pozitív szám. Bizonyítsuk be, hogy
xt(x - y)(x - z) + yt(y - x)(y - z)+ zt(z - x)(z - y) 0. 0.
|
|
| [2788] Lóczi Lajos | 2008-12-04 20:59:37 |
 Sőt, bonyolultabban is megkapható :), pl. úgy, mint két ponthalmaz a síkon, ahol a kétváltozós távolságfüggvényt kell minimalizálni. Ennek a módszernek az "előnye", hogy a [2778]-as hozzászólásból a [2779]-esbeli feladatot gyártotta.
|
| Előzmény: [2787] Valezius, 2008-12-04 15:05:49 |
|
| [2787] Valezius | 2008-12-04 15:05:49 |
 Egyszerűbben is megkapható.
Egyrészt ax=x Másrészt: ax*ln a=1 Ha a másodikban beírjuk ax helyére x-et, akkor x*ln a=1. Az első pedig átírható, mint ex*ln a=x Azaz e1=x Visszaírva pedig 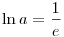 Azaz Azaz 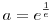
|
| Előzmény: [2786] rizsesz, 2008-11-26 21:46:38 |
|
| [2786] rizsesz | 2008-11-26 21:46:38 |
 A feladat másképpen az, hogy x1/x = a-nak pontosan 1 megoldása legyen. x1/x deriváltja egyedül az x=e helyen 0 (már ha nem számoltam el, de nekem x1/x-2 * (1-ln x) jött ki. Ez pedig lokális (és amúgy abszolút) maximumot eredményez, tehát ezen érték mellett egy jó a érték van. Jaj. tehát vissza kell írni x helyére és kijön az a=e1/e . Jaj. Már csak azt a sejtést kell igazolni, hogy ha x a végtelenhez tart, akkor x1/x végtelenben vett határértéke 1. Ugyanis x1/x x=1 esetén 1, tehát mivel szigorúan monoton növekvő 1 és e, illetve szigorúan monoton csökkenő e és + végtelen között, továbbá folytonos, így az e-nél felvett értéken kívül minden értéket kétszer vesz fel.
|
| Előzmény: [2775] Lóczi Lajos, 2008-11-25 23:48:43 |
|
|
|
|
| [2782] rizsesz | 2008-11-26 17:02:59 |
 e x. hatványával és (-1)-gyel felszorozva olyan függvények összege lesz az egyenlet bal oldala, amelyek mindegyik szogorúan monoton növekvő. Mivel x=0 megoldás, továbbá eleme az értelmezési tartománynak, így ez az egyetlen megoldás.
|
| Előzmény: [2779] Lóczi Lajos, 2008-11-26 00:33:28 |
|
|
| [2780] Euler | 2008-11-26 08:35:20 |
 A távolsága a két függvénynek négyzetgyök 2, hiszen ezek egymás inverzei, igy mindkét függvénynek a távolsága megegyezik az y=x egyenestől ennek a távolságát pl. a logaritmusfüggvénytől már meg tudjuk határozni deriválással, mert a (0,1) pontba húzott érintő meredeksége éppen egy(könnyen ellenőrizhető), ezen érintő és az y=x távolságának kétszerese pedig éppen a keresett távolság. Az egyenletnek nyilván megoldása az x=0. Rendezzük át az egyenletet úgy, hogy az utolsó két tagot átvisszük a jobb oldalra, igy, ha x>0, akkor a bal oldal negativ, a jobb oldal pozitiv, hasonlóan, ha x<0, akkor a bal oldal pozitiv, a jobb oldal negativ, igy újabb megoldások már nincsnek.
|
| Előzmény: [2778] Lóczi Lajos, 2008-11-26 00:29:09 |
|
| [2779] Lóczi Lajos | 2008-11-26 00:33:28 |
 335. feladat. Oldjuk meg a valós számok halmazán az
e-x-e2x-x-xex=0
egyenletet.
|
|
| [2778] Lóczi Lajos | 2008-11-26 00:29:09 |
 334. feladat. Határozzuk meg a (természetes alapú) exponenciális függvény és logaritmusfüggvény grafikonjainak távolságát.
|
|










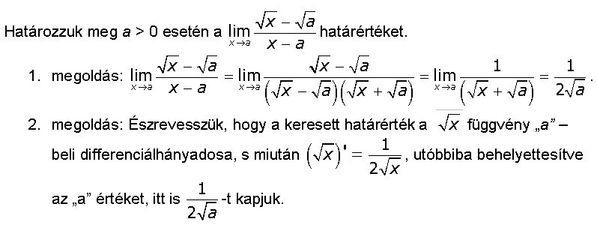

 0, x, y, z pedig pozitív szám. Bizonyítsuk be, hogy
0, x, y, z pedig pozitív szám. Bizonyítsuk be, hogy