| [3539] Róbert Gida | 2012-01-12 00:47:15 |
 Első feladatra: ha a háromszög tompaszögű, akkor trivi, mert a szorzat akkor negatív. Egyébként számtani-mértani egyenlőtlenség, majd Jensen egyenlőtlenség a [0,Pi]-n konkáv cos fv-re
Második feladatra nincs tippem.
Utolsó feladat: cos-ra használhatod a cos tételt, 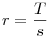 és és 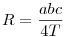 , ahol T a terület, s a félkerület. Továbbá T-re a Héron képletet. Ekkor mindenhol már csak a,b,c szerepel, azaz egy azonosságot kell kapnod, ha mindent behelyettesítesz. (itt már nem is lényeges, hogy ezek egy háromszög oldalai is.) , ahol T a terület, s a félkerület. Továbbá T-re a Héron képletet. Ekkor mindenhol már csak a,b,c szerepel, azaz egy azonosságot kell kapnod, ha mindent behelyettesítesz. (itt már nem is lényeges, hogy ezek egy háromszög oldalai is.)
|
| Előzmény: [3537] onkiejoe, 2012-01-11 23:45:20 |
|
|
| [3537] onkiejoe | 2012-01-11 23:45:20 |
 Sziasztok! Lenne néhány feladatom, amin jó pár napja ülök, de egyszerűen nem tudom lebirkózni őket. Már mindent megpróbáltam, amit tudtam, de nem tudok rájönni a megoldás kulcsára. Két szélsőérték-feladat (igazolni kell minden háromszögre, melynek szögei A, B és C, valamint megmondani, hogy milyen A, B, C esetén van egyenlőség):
cos(A)*cos(B)*cos(C) 1/8 1/8
(itt a * sima szorzásjel akar lenni)
cos(A)+cos(B)+cos(C) 3/2 3/2
A feladat "trükkje" az lenne, hogy nem szabad deriválást alkalmazni. Egyébként innen származnak: (12. és 9. feladat) És van még egy, ez már nem szélsőérték (szintén bizonyítandó, az előzőektől függetlenül):
cos(A)+cos(B)+cos(C)=(r+R)/R
(r: beírható kör sugara, R: körülírt kör sugara)
Minden segítséget, választ, és esetlegesen megoldást is előre köszönök!
(És elnézést kérek, hogy nem igazán ismerem ki magam a program kód- és jelrendszerén.)
O.
|
|
|
|
|
| [3533] jonas | 2011-12-18 18:40:56 |
 Az n pozitív egész számot szeretnénk előállítani. Ehhez keressünk egy p prímet, ahol n<p. Ekkor bármilyen k természetes számra n=(pk+n)-pk. Mármost (pk+n) relatív prím pk-tól, mert az utóbbinak az egyetlen prímosztója a p, az előbbi pedig nem osztható p-vel.
|
| Előzmény: [3529] Sirpi, 2011-12-18 10:51:32 |
|
|
|
| [3530] Róbert Gida | 2011-12-18 11:57:45 |
 Legyen B=4*n2+4*n+1=(2*n+1)2 és A=4*n2+5*n+1=(n+1)*(4*n+1). Ekkor A-B=n, itt A,B összetett a faktorizáció miatt. És relatív prímek, hiszen:
lnko(A,B)=lnko(A-B,B)=lnko(n,4n2+5n+1)=lnko(n,1)=1
|
| Előzmény: [3529] Sirpi, 2011-12-18 10:51:32 |
|
| [3529] Sirpi | 2011-12-18 10:51:32 |
 A feladatom nem teljesen explicit, de sebaj.
Adjunk minél egyszerűbb konstruktív bizonyítást arra, hogy minden pozitív egész szám előáll két relatív prím összetett szám különbségeként.
|
|
|
| [3527] Fálesz Mihály | 2011-12-07 11:05:19 |
 L'Hospital szabállyal:
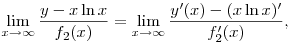
ha 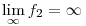 és a jobboldali határérték létezik. és a jobboldali határérték létezik.
Azt már tudjuk, hogy ln y=ln x+ln ln x+o(1).
y'(x)-(x.ln x)'=ln y-ln x-1=ln ln x+O(1).
Olyan f2 kell tehát, aminek a deriváltja kb. ln ln x. Az x.ln ln x ilyen, mert a ln ln x lassan nő, de parciális integrálással is megtalálhatnánk:
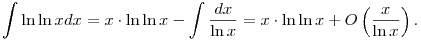
|
| Előzmény: [3526] Lóczi Lajos, 2011-12-07 10:14:29 |
|
|
|
| [3524] Lóczi Lajos | 2011-12-07 04:27:31 |
 Egyelőre én is pont eddig jutottam. Igen, jonas, a bizonyítás talán 1 oldalban összefoglalható lenne, tehát teljesen elemi megfontolásokat használtam csak (az Li függvényről is).
Ha f1(x):=xln (x), akkor tehát eddig azt tudjuk, hogy 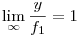 . Az is egyszerűen adódik, hogy . Az is egyszerűen adódik, hogy 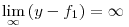 . .
A továbblépéshez keresendő tehát egy f2, hogy 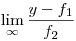 egy véges, nemnulla valós szám legyen. Aztán általában fk, hogy egy véges, nemnulla valós szám legyen. Aztán általában fk, hogy 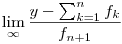 létezik, véges és nemnulla. létezik, véges és nemnulla.
|
| Előzmény: [3521] nadorp, 2011-12-06 15:36:04 |
|
|
|
|
| [3520] Lóczi Lajos | 2011-12-01 19:51:40 |
 Igen, én is erre. A további kérdés persze az, hogy 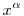 helyett a nevezőbe milyen függvényt írjunk, hogy véges, nemnulla limeszt kapjunk a végtelenben. Vagyis adjuk meg az y függvény aszimptotikus sorának elejét. helyett a nevezőbe milyen függvényt írjunk, hogy véges, nemnulla limeszt kapjunk a végtelenben. Vagyis adjuk meg az y függvény aszimptotikus sorának elejét.
|
| Előzmény: [3519] nadorp, 2011-12-01 17:04:13 |
|
|
| [3518] Lóczi Lajos | 2011-11-28 21:14:23 |
 Tekintsük az
y'(x)=ln (y(x))
differenciálegyenlet azon megoldását, amelyre y(0)=2.
Határozzuk meg a
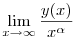
határértéket, ahol  egy adott valós szám. egy adott valós szám.
|
|
| [3517] lorantfy | 2011-11-11 15:54:05 |
 Na előtűntek az igazi adatok: az utaskihasználásnak itt nincs értelme, a billentési idő 0.01 h/t (és nem t/h), vagyis a 15t lerakodása 0,15 h=9 perc. A 30 km/h az 2 perces km-eket jelent, tehát egy kocsi menetideje 36 perc+9perc rakodás=45 perc. Ezalatt (45x60):400=6,75 kocsit rakodnak meg. Szóval a folyamat semmiképpen sem lesz folyamatos. Ha 7 kocsi van, akkor a rakodógépnek kell várakoznia, ha meg 8, akkor a kocsiknak.
|
| Előzmény: [3514] szorgos diák, 2011-11-08 22:09:37 |
|
| [3516] lorantfy | 2011-11-10 16:07:39 |
 Legyen a kocsik átlagsebessége 60 km/h és tartson a lerakodás 2 percig (mert csak odaáll és ledönti). Akkor a 9 km megtétele oda-vissza, meg még a lerakodás éppen 20 perc. Egy kocsit 10x40=400 sec= 6 perc 40 sec-ig pakolnak. Vagyis a szállítási idő pont 3 rakodási idővel egyenlő. Tehát amíg az egyik kocsi szállít, éppen 3 másik kocsit raknak meg mire visszaér, szóval 4 kocsi kell. Én ilyen adatokat adtam volna meg és tartok tőle, hogy az eredeti adatok is ezek voltak.
|
| Előzmény: [3514] szorgos diák, 2011-11-08 22:09:37 |
|
|




 1/8
1/8




 egy adott valós szám.
egy adott valós szám.
