| [732] Atosz | 2005-01-20 15:01:26 |
 Sziasztok!
Még mindig (valószínűleg még sokszor) visszakanyarodnék a gyógyszeres példához. Légyszi véleményezzétek a következő gondolatot:
Ha a gyógyszerek száma viszonylag nagy és pl. csupa egészekből indulunk ki, akkor mindaddig, amíg az egészek vannak túlsúlyban, addig nagy valséggel azokat húzzuk, ám ennek hatására növekszik a felek száma. Amennyiben viszont a felek túlsúlyba kerülnének, akkor többször húzunk azokból és így viszont az egészek aránya növekszik meg. Ha elegendően nagy értékekből indulunk ki, akkor nagy valószínűséggel beáll a szem-típusok közt egy egyensúlyi állapot, amit a rendszer nem enged túlzottan kilengeni semelyik irányba. Ebből az következik, hogy pe,f értéke nagy e és f esetén felveszi pe*,f* értéket és azzal közel egyenlő is lesz. Így a feladat bizonyos értékek esetén statisztikai és határértékszámítási eszközökkel is elemezhető lesz.
Lehet, hogy pe,0 értéke 'e tart végtelen' esetén, tart valamilyen meghatározott értékhez, illetve ez más pe,f esetén is hasonló lehet?
Az általános rekurziós képletet pe,f esetén beírtam egy excell táblába, mely kiszámította ezeket. Az adatokat most vizsgálom, majd jelentkezem...
Atosz
|
|
|
| [730] jonas | 2005-01-20 10:17:49 |
 Szerintem is.
A Reiman Geometria[1] a 19. fejezetben (337. oldal a régi kiadásban) szintén az utóbbi képletet adja: a C-K modellen két pont távolsága  (P,Q)=(k/2)|ln ((UP/UQ)/(VP/VQ))| ahol U,V a PQ húr végpontjai. Leírja azt is, hogy az (UP/UQ)/(VP/VQ) kettősviszony mindig pozitív, mert a PQ szakasz az UV szakasz belsejében van, ezért a logaritmálás értelmes. (P,Q)=(k/2)|ln ((UP/UQ)/(VP/VQ))| ahol U,V a PQ húr végpontjai. Leírja azt is, hogy az (UP/UQ)/(VP/VQ) kettősviszony mindig pozitív, mert a PQ szakasz az UV szakasz belsejében van, ezért a logaritmálás értelmes.
[1] Reiman István, A geometria és határterületei. 1986, Gondolat, Budapest
|
| Előzmény: [729] Laci, 2005-01-19 20:14:46 |
|
| [729] Laci | 2005-01-19 20:14:46 |
 Nekem lenne egy kérdésem a Cayley-Klein modellt illetően. Az ehavi Kömalt olvasgatván rábukkantam a
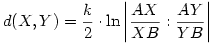
képletre, ami a fent említett modellben található két pont távolságát adja meg. Az lenne a kérdésem, hogy ez nincsen-e elírva, mert szerintem a helyes képlet így szólna:
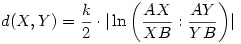
Márcsak azért is, mert a 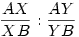 tag sohasem lehet negatív, de ennek az e alapú logaritmusa igen. Az én képletem szerint X és Y tetszőlegesen felcserélhető, az újságban szereplő szerint nem. A kérdésem: igazam van? tag sohasem lehet negatív, de ennek az e alapú logaritmusa igen. Az én képletem szerint X és Y tetszőlegesen felcserélhető, az újságban szereplő szerint nem. A kérdésem: igazam van?
|
|
| [728] rizs | 2005-01-19 15:13:38 |
 nekem inkább egy olyan ötletem volt, hogy az esetek párbaállíthatóak, de közben rájöttem, hogy elvi hibás a dolog. mivel azonban az 1/2 jó, valószínűleg mégis erről lehet szó :)
|
|
| [727] jenei.attila | 2005-01-19 14:47:07 |
 Jelöljük pn-nel annak a valószínűségét, hogy n utas esetén az utolsó a saját helyére ül. Nyilván p2=1/2. Annak a valószínűsége, hogy az őrült a helyére ül, az 1/n. Az hogy a 2. utas helyére ül, szintén 1/n. Ha az őrült a második utas helyére ült, akkor a 2. utas lesz az új őrölt (a helye az 1. hely lenne), az utasok száma pedig n-1. Ha az őrült 1/n valószínűséggel a 3. utas helyére ült, akkor a 3. utas lesz az új őrült, és az utasok száma n-2,...s.í.t. Vagyis 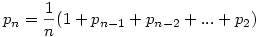 . Ebből teljes indukcióval könnyen kiszámítható, hogy pn=1/2. . Ebből teljes indukcióval könnyen kiszámítható, hogy pn=1/2.
|
| Előzmény: [726] Atosz, 2005-01-19 12:26:08 |
|
|
|
| [724] Atosz | 2005-01-18 23:11:16 |
 Kedves Viktor!
Sajnos nem jó a válasz! Ennél azért egy kicsit bonyolultabb ez a feladat. Először 1 "őrültre" próbáld megoldani. Gondold végig, hogy sorba állnak az ajtónál, elől az 1-es, majd a 2-es... végül pedig a 100-as. Most az 1-es az "őrült" (gondolom érzed, hogy a sorszámozásnak nincs jelentősége), aki berohan és leül pl. a 38-as székre. Ekkor 2-37-ig nincs gond, ám jön a 38-as akinek foglalt a helye...Ha az "őrült" a 100-as helyére ült volna, akkor 0 valséggel ül a helyére a 100-as. Ezt a gondolatmenetet kövesd '38' nélkül általánosan.
Egy darabig még hagyok időt mindenkinek - aztán közzéteszem a megoldást!
Minden jót: Atosz
|
| Előzmény: [723] xviktor, 2005-01-18 18:13:48 |
|
| [723] xviktor | 2005-01-18 18:13:48 |
 Hello Atosz!
Szerintem a feladat kissé egyszerűbb. Véleményem szerint az mindegy, hogy hány őrült van köztük, és szerintem annak az esélye, hogy a 100. utas a helyére tud ülni mindig 1/n, így 100 utasnál 0,01.
Üdv: Viktor
|
| Előzmény: [721] Atosz, 2005-01-17 23:26:18 |
|
|
| [721] Atosz | 2005-01-17 23:26:18 |
 Kedves Lóczi Lajos és többiek!
Egész ügyes ez a Mathematica, a képlet tényleg zártabb, és módot ad p2,k egy elég jó felső becslésére.
Előszedtem a harmonikus sor és a számtani közép közti egyenlőtlenséget, miszerint:
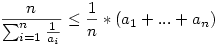
Itt most n=k+2 és ai=i, amit ha elkezdünk alakítgatni, kapjuk, hogy
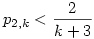
Szeretnék azoknak akiknek nem fekszik teljesen ez a gyógyszeres feladat egy új példát adni a valség köréből, ami nem túl nehéz, ám a megoldása miatt az egyik kedvencem:
100 utas várakozik a reptéren, hogy végre beszállhassanak. A gépen 100 ülőhely van, mindenkinek máshová szól a jegye. Az első utas "őrült" nem törődik a jegyével, s beszálláskor véletlenszerűen elfoglal egy széket. Az összes többi utas "normális" és a helyére fog ülni, feltéve, ha ott még nem ül senki. Ha a helyük foglalt, akkor ők is véletlenszerűen választanak egy széket. (az utasok egymás után egyesével szállnak a gépre)
Mekkora a valsége annak, hogy a 100. utas a helyére tud ülni? Mi a helyzet n utas és abból k őrült esetén?
|
| Előzmény: [720] Lóczi Lajos, 2005-01-17 17:51:35 |
|
| [720] Lóczi Lajos | 2005-01-17 17:51:35 |
 A Mathematicába beírtam a p2,k-ra vonatkozó rekurzív képletet, és az alábbi alakot kaptam vissza, ami talán kicsit egyszerűbb, mint az említett:
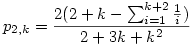
Látható, hogy a (k+2)-edik harmonikus szám szerepel a képletben, tehát ennél "zártabb" alak p2,k-ra szerintem nem várható.
|
| Előzmény: [719] Atosz, 2005-01-17 16:52:17 |
|
| [719] Atosz | 2005-01-17 16:52:17 |
 Sziasztok!
Újabb "Rés a pajzson..." a gyógyszeres feladatban. Kis lépés, de ez is valami.
Sokáig próbálkoztam a pk,k vizsgálatával de nem bírtam zárt, "szumma" nélküli alakra hozni. Arra gondoltam, hátha alulról építkezve, speciális eseteket vizsgálva érnénk el eredményt.
Megnéztem a p1,k (1 egész, k fél) valségét. Ilyenkor abban az esetben marad egész, ha végig feleket húzunk egymás után, azaz
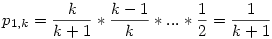
Ekkor felírtam p2,k-ra az eredeti rekurziós képletet, azaz:
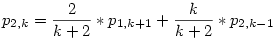
Beírva p1,k+1 helyére az 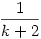 értéket, kapjuk hogy: értéket, kapjuk hogy:
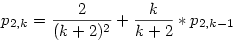
Rengeteg egyváltozós függvényt vizsgáltam meg, hogy eleget tesz-e az előző függvényegyenletnek, de nem jártam sikerrel. Ekkor p2,k-1-et tovább alakítottam p2,k-2-vé és így tovább, amíg el nem érünk p2,0-ig, melynek értéke 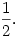 A kapott hosszú szörnyet addig néztem, amíg ki nem jött, hogy: A kapott hosszú szörnyet addig néztem, amíg ki nem jött, hogy:
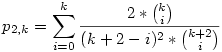
Jó lenne ennek egy zárt alakot felírni, de nekem már ez is tetszik. Viszonylag jól lehet vele számolni is:
pl. 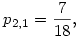 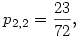 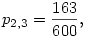
További jó munkát!
|
|
| [718] Bubu | 2005-01-17 15:13:44 |
 Hello Mindenki!
A kihalási probléma a következő: Egy szigetre egy férfi érkezik. A szigeten tetszőleges mennyiségben rendelkezésre állnak nők (19. századi a feladat). Egy férfi p(0) valséggel 0, p(1) valséggel 1, stb., p(n) valséggel n nemzőképes fiú utódot hoz létre (Ezen valségek összege 1.). Mi a valószínűsége, hogy a populáció véges idő alatt kihal?
Szerintem nem sok köze van egymáshoz a kettőnek. Az biztos, hogy a kihalási problémára is felírható egy rekurzió, ami nem oldható meg, és ott az trükk, hogy a generátorfüggvény kompozicóit kell vizsgálni. Sajnos töbet nem tudok én se róla, mert csak egy rövid folyosói beszélgetésben hallottam a problémáról, de ha kell majd utánakérdezek később. Nem tudom, hogy ezzel segítettem-e, mindenesetre most nem érek rá ezzel foglalkozni, mert analízis szigorlatra készülök gőzerővel.
Üdv: Bubu
|
|
| [717] Atosz | 2005-01-15 00:22:21 |
 Sziasztok!
Visszatérve a gyógyszeres feladathoz, sikerült előtúrnom a régi jegyzeteimet, a benne lévőket közreadom, hátha közös erővel közelebb jutunk a megoldáshoz.
Kézi erővel viszonylag egyszerű a gyógyszerfogyási fát felírni. Pl. n=4-re - írjuk ezt úgy, hogy (4,0) -, ebből előbb (3,1) lesz, majd növesztjük az ágakat: 3/4 valséggel megyünk (2,2)-re és 1/4 valséggel (3,0)-ra. Ezt egészen addig folytatjuk, amíg a fa ágainak végén 1 egész, vagy 1 fél szem lesz. Összeszorozzuk az egész végű ágon lévő valségeket, majd az ilyen ágak értékeit összeadjuk, megkapjuk a keresett valószínűséget.
Ha sehol sem számoltam el, akkor n=2-re p=1/2, n=3-ra p=7/18, és n=4-re p=97/288. Persze ember legyen a talpán, aki mindezt sz.gép nélkül n=100-ra megcsinálja.
Ekkor elkezdtem az ált. problémát vizsgálni. Legyen 'e' az egész, míg 'f' a fél szemek száma. Annak a valószínűsége, hogy ebből egész marad, az legyen pe,f. Az általános rekurzív formula így:
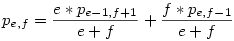
Ezt több oldalon keresztül alakítgattam, de nem bírtam vele. Ekkor elkezdtem egy picit specializálni, és megvizsgáltam azt az esetet, amikor induláskor megegyezik az egész és a felek száma, azaz megnéztem pk,k-t. Annak reményében tettem mindezt, hátha ezek segítségével jutunk az ált. eset nyomára.
Sikerült egy szép zárt alakot felírnom (ami még mindig rekurzív, de már lemegy 1-ig)
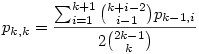
Ez pl. p4,4-re: (és a nevezővel átszorozva)
70*p4,4=35*p3,5+20*p3,4+10*p3,3+4*p3,2+p3,1
Egyelőre ennyi. Szerintem ez egy igen érdekes probléma, ne adjuk fel, előbb utóbb meglesz!
|
| Előzmény: [716] jenei.attila, 2005-01-14 13:40:18 |
|
|
| [715] jenei.attila | 2005-01-14 13:35:26 |
 Ezzel szerintem az a baj, hogy feltételezed, bármely sorozat előfordulása ugyanolyan valószínű, holott ez nem igaz. A kedvező eset/összes eset képlet pedig csak ekkor alkalmazgató. A képleted sajnos n=2 re sem jó, mert 1/3-ot ad, a helyes érték pedig 1/2.
|
| Előzmény: [714] nadorp, 2005-01-14 13:05:26 |
|
| [714] nadorp | 2005-01-14 13:05:26 |
 A "kihalási probléma" felvetése nagyon szimpatikusnak tűnik nekem is,hétvégén én is utánanézek. Addig is egy újabb kísérlet elemi megoldásra,ezt is vitára bocsátom.
Ki fogjuk használni azt, hogy a k-dik lépésben kivett tabletta milyenségének - egész vagy fél - valószínűsége csak attól függ, hogy előtte hány egész tablettát vettünk ki. Írjunk 1-et ha egész tablettát, és írjunk 0-át, ha fél tablettát vettünk ki az üvegből. Folytassuk ezt mindaddig, amíg ki nem ürül az üveg. Ezzel kaptunk egy 2n hosszú, 1-t és 0-t tartalmazó sorozatot, mely 1-gyel kezdődik, 0-ra végződik,ugyanannyi 1 és 0 van benne, és igaz rá, hogy minden 1 k k 2n indexre az első k elem között legalább annyi 1-es van, mint 0. Fordítva, az előbbi tulajdonságú tetszőleges sorozat egyértelműen meghatároz egy tabletta kivételt. Jelölje xn az ilyen tulajdonságú sorozatok számát. Számunkra az a kedvező eset, ha a sorozat 10-ra végződik. Ezen esetek száma viszont nyilván xn-1. A keresett valószínűség tehát 2n indexre az első k elem között legalább annyi 1-es van, mint 0. Fordítva, az előbbi tulajdonságú tetszőleges sorozat egyértelműen meghatároz egy tabletta kivételt. Jelölje xn az ilyen tulajdonságú sorozatok számát. Számunkra az a kedvező eset, ha a sorozat 10-ra végződik. Ezen esetek száma viszont nyilván xn-1. A keresett valószínűség tehát 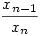 . Most már "csak" xn értékét kell meghatározni. Innen kezdve "lestem" Vilenkin: Kombinatorika c. könyvéből, a "Pénzváltási probléma" nevű rész pont ezzel a foglalkozik. Itt azt kapjuk, hogy . Most már "csak" xn értékét kell meghatározni. Innen kezdve "lestem" Vilenkin: Kombinatorika c. könyvéből, a "Pénzváltási probléma" nevű rész pont ezzel a foglalkozik. Itt azt kapjuk, hogy 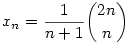 . Azaz a keresett valószínűség . Azaz a keresett valószínűség 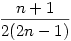
|
|
| [713] jenei.attila | 2005-01-14 11:40:40 |
 Még régen a tiszta kihalási problémából vizsgáztam sztochasztikus folyamatok című tantárgyból, de sajnos már csak ennyire emlékszek, meg arra, hogy meglehetősen nehéz probléma. Egyébként szerintem is két dimenziós bolyongásról van szó, na majd utánanézek.
|
| Előzmény: [712] Atosz, 2005-01-14 11:27:08 |
|
| [712] Atosz | 2005-01-14 11:27:08 |
 Kedves jenei.attila!
Segítenék, ha tudnék, de ennek a feladatnak én sem tudom a megoldását. Előkeresem majd a papírjaimat, amit egy unalmas előadáson firkálgattam és megpróbálok majd abból valami értelmeset közreadni, hátha valakinek segít. Egyszer egy ismerősöm elmesélte ezt a feladatot egy valség tanárnak, aki felületesen megnézve azt mondta rá, hogy a kihalási problémára (???) hasonlít. Nem tudom, hogy mi az, és azóta sem néztem utána, de hátha ez támpont lehet valakinek. Persze lehet, hogy semmi köze ahhoz.
|
| Előzmény: [711] jenei.attila, 2005-01-14 11:17:01 |
|
| [711] jenei.attila | 2005-01-14 11:17:01 |
 Szia Atosz!
A gyógyszeres feladat szerintem is nehéz (legalábbis nekem), én is csak egy rekurzív képletet tudok felírni, és egy kis programot is írtam, amely megadja minden lehetséges állapot valószínűségét. Szerintem elképzelhető, hogy nem is adható zárt képlet a keresett valószínűségre. Még azért nem adtam fel, de segíthetnétek.
|
|
| [710] lorantfy | 2005-01-13 13:12:11 |
 141. feladat megoldása: Vegyünk 100100 embert aki ott nyaralt. Közülük 100 kapott fertőzést 100000 egészséges.Hazaérve mind megvizsgáltatja magát.
Az 100000 egészséges közül 2% 2000 kap pozitív eredményt. A 100 beteg közül 99%=99 fő pozítiv. Összesen tehát 2099 ember kap pozitív eredményt. Te ezek között vagy, hiszen pozitív eredményt kaptál.
Tehát annak a valószínüsége, hogy beteg vagy 99/2099=4,72%.
|
| Előzmény: [708] rizs, 2005-01-13 00:46:31 |
|
|
| [708] rizs | 2005-01-13 00:46:31 |
 141. feladat, és eléggé közismert is, de nem igazán tudom :) Egy afrikai országban nyaralsz. Hazaérve megtudod, hogy az itt nyaralók közül minden 1001-edik ember egy vírusfertőzést szed össze. Hazaérve megvizsgáltatod magadat, és pozitív eredményt kapsz. A tesztől azt mondják, hogy a megbízhatósága: - ha valóban beteg vagy 99 - ha egészséges vagy 98 Mennyi az esélye, hogy tényleg beteg vagy?
142. feladat :) közismert, hogy 10-féle embertípus van, melyek ezek? :)
|
|





 (P,Q)=(k/2)|ln ((UP/UQ)/(VP/VQ))| ahol U,V a PQ húr végpontjai. Leírja azt is, hogy az (UP/UQ)/(VP/VQ) kettősviszony mindig pozitív, mert a PQ szakasz az UV szakasz belsejében van, ezért a logaritmálás értelmes.
(P,Q)=(k/2)|ln ((UP/UQ)/(VP/VQ))| ahol U,V a PQ húr végpontjai. Leírja azt is, hogy az (UP/UQ)/(VP/VQ) kettősviszony mindig pozitív, mert a PQ szakasz az UV szakasz belsejében van, ezért a logaritmálás értelmes. 

 -hoz.
-hoz. k
k
