| [74] Hajba Károly | 2003-11-14 13:01:02 |
 Visszatérek a biliárdgolyós feladathoz, mivel úgy tűnik számomra, még sok érdekes dolgot lehet kihozni belőle.
- [39] hozzászólásbeli Gáti Baetrix Zoltán által közzétett táblázata a nehezebb változatnak éppen nem felel meg, de ha a 3. mérésben a 8-as golyót a 12-esre cseréljük, már tökéletes.
- [52]-beli Bubu hozzászólásában a több eltérő golyó felé általánosít. Bennem pedig már korábban felmerült egy másik általánosítási lehetőség, miszerint valamely golyó(k)ról állítjuk, hogy nem tér el és ez alapján, hogy változik a mérhető golyók száma. Továbbá mi a helyzet a kevesebb ill. több mérési számok esetén.
16. feladat: Ha n a mérések száma, mennyi a legnagyobb g(n) golyók száma, mely esetén még meghatározható a hibás golyó és annak eltérése is?
17. feladat: Ha 2-szer mérhetünk, hány biztosan nem hibás golyót kell ismernünk, hogy a lehető legtöbb ismeretlen golyó közül tudjuk kiválasztani az egyetlen hibás golyót és eltérését?
Hajba Károly
|
|
| [73] lorantfy | 2003-11-14 12:56:58 |
 Kedves Károly, Zoli és Kockarajongók!
Feltúrtam a fizika szertárt és megtaláltam a Fizikai Szemle 82/2-es számában a cikket. Jövő héten beszkennelem és recognitázom - szóval nyomtatott formából elektronikus formába alakítom. (Jó lenne erre egy egyszerű szó - a digitalizálni talán nem a legszerencsésebb - ha tudtok jobbat írjátok meg!) Az érdeklődőknek tudom küldeni.
|
| Előzmény: [72] Hajba Károly, 2003-11-14 08:40:05 |
|
| [72] Hajba Károly | 2003-11-14 08:40:05 |
 Kedves Zoli!
Isten hozott a kockabűvöltek táborába!
Beszkennelem a cikket, de feltételezem, hogy a Fizikai Szemlebeli cikk részletesebb lehet. Ti. késöbb jelent meg és többen jegyezték.
> Ti láttatok már 4*4*4 Rubik-kockát?
Anno volt a kezemben egy, talán kölcsön is kaptam egy hétre, de lehet, hogy az a dodekaéder volt. Ki tudja, ezirányú emlékeimet belepte már a rozsda. Tény, hogy nem bírtam vele :o(
Üdv: Károly
|
| Előzmény: [71] SchZol, 2003-11-14 05:48:40 |
|
| [71] SchZol | 2003-11-14 05:48:40 |
 Kedves Károly!
Engem érdekelne a Rubik-kockás cikk, ha beszkenneled. Nagyon szeretem a Rubik-kockát, hetente egy párszor mindig kirakom. Ti láttatok már 4*4*4 Rubik-kockát? Sajnos Én még nem láttam, csak hallottam róla.
Üdv, Zoli
|
|
| [70] Hajba Károly | 2003-11-13 23:50:18 |
 Kedves László!
Nem azt a cikket ismerem, hanem a könyvbelit (A bűvös kocka - Gondolat - 1981), amit még csak Marx jegyzett (no nem a Tőkés :o).
A 'spin' pedig, hát... anno szerettem a fizika ezen részét is.
Ha érdekel a könyvbeli cikk, megpróbálhatom beszkennelni és drótpostán elküldeni.
Üdv: Hajba Károly
|
| Előzmény: [68] lorantfy, 2003-11-13 23:16:47 |
|
| [69] lorantfy | 2003-11-13 23:22:51 |
 Az 5. feladatra: még nem írtunk megoldást. Az eredeti szöveg: Adott 100 láda mindegyikben 1000 db 2 grammos 1 forintos, kivéve egyet amiben 1 grammosak az 1 forintosok. Legkevesebb hány mérésből tudjuk eldönteni melyik ládában vannak a selejtes egy forintosok, ha minden láda ugyanúgy néz ki, és csak egy egykarú mérlegünk van.
Aki nem ismeri annak érdemes átgondolni a trükköt: Sorszámozzuk meg a ládákat 1-100-ig és minden ládából tegyünk fel a mérlegre annyi forintost amennyi a láda sorszáma. Ezt mérjük le. Ha minden ládában 2 grammos érmék lennének akkor (1+100)x100 = 10100 grammot kellene mérnünk. Amennyivel kevesebbet mérünk annyi a keresett láda sorszáma.Tehát egy mérés elegendő.
Az eredeti kitűző – Sch Zoli – nehezítése:
15. feladat: Hány mérés szükséges, ha a 100 közül két ládában vannak 1 grammos forintok.
|
| Előzmény: [6] SchZol, 2003-11-01 22:12:06 |
|
| [68] lorantfy | 2003-11-13 23:16:47 |
 Kedves Lajos!
Örülök, hogy feltetted a megoldást. Úgy néz ki a „fiatalok” tényleg nem harapnak erre a témára. A „spin” szóhasználatból arra következtetek, hogy talán Te is olvastad a Fizikai Szemlében megjelent cikket (21 éve) Ha esetleg valakinek meglenne elektronikus formában köszönettel venném:
MARX GY., GAJZÁGÓ É., GNÄDIG P., ZÁMBÓ V.: A bűvös kocka univerzuma - Fizikai Szemle 32 (1982) 73-77
|
| Előzmény: [59] Hajba Károly, 2003-11-13 00:09:23 |
|
|
|
| [65] Lóczi Lajos | 2003-11-13 18:57:33 |
 Álljon itt a háromszöges feladat egy általánosítása: az alapon fekvő szögek a 80o helyett legyenek  , a 60o-os BAE szög helyett legyen , a 60o-os BAE szög helyett legyen  , a 70o-os ABD szög pedig legyen most , a 70o-os ABD szög pedig legyen most  ; ezekről tehát azt tesszük fel csak, hogy 0< ; ezekről tehát azt tesszük fel csak, hogy 0< <90o, 0< <90o, 0< < < , 0< , 0< < < . Jelölje továbbá a keresett BDE szöget . Jelölje továbbá a keresett BDE szöget  . A rövidség kedvéért egy x szög tangensét jelölje . A rövidség kedvéért egy x szög tangensét jelölje  x. x.
Ekkor elemi koordinátageometriai érvelés mutatja, hogy
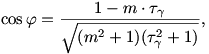
ahol 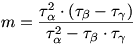 . .
Az  =80o, =80o,  =60o, =60o,  =70o értékeket behelyettesítve, "némi" algebrai egyszerűsítés után például az alábbi alakot kapjuk (ki-ki maga is megpróbálkozhat eljutni idáig): =70o értékeket behelyettesítve, "némi" algebrai egyszerűsítés után például az alábbi alakot kapjuk (ki-ki maga is megpróbálkozhat eljutni idáig):
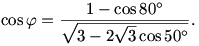
13. feladat. Bizonyítsuk be, hogy a fenti kifejezés jobb oldala cos 20o.
|
| Előzmény: [63] Kós Géza, 2003-11-13 14:25:51 |
|
| [64] jenei.attila | 2003-11-13 17:28:42 |
 Ötletes a hivatkozott KÖMAL-ban közölt 18 szöges megoldás, bár abban a feladatban az ABD szög 50 fok. Valószínűleg a módszer alkalmazható akkor is, mikor ABD szög=70 fok. Kiváncsi lennék a 18 szöges megoldástól független megoldásra ABD=50 fok esetén.
|
| Előzmény: [63] Kós Géza, 2003-11-13 14:25:51 |
|
|
| [62] lorantfy | 2003-11-13 13:51:17 |
 Kedves Csillag és Attila!
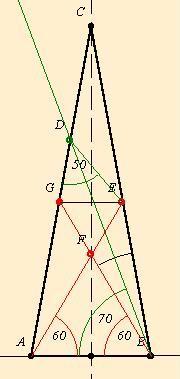
Szép a megoldás! Egy ábrát megérdemel.
|
 |
|
| [61] jenei.attila | 2003-11-13 10:34:03 |
 Szia Csillag!
Szép megoldás, gratulálok. Egy két apróbb megjegyzést tennék. Amikor felírtad, hogy GD=GF=GE, innen már azonnal következik, hogy GDE szög = GED szög = 50 fok, de ADB szög = 30 fok, amiből EDB szög = 20 fok. Csak egy kis egyszerűsítés. Az én megoldásom is hasonló, megtartva a Te jelöléseidet, a következő: DC/GD=CB/CE=AB/GE. A GE félegyenesen vegyük fel H pontot úgy, hogy GH=GC legyen. Ekkor EH=GH-GE=GB-GF=FB=AB. Vagyis DC/GD=AB/GE=EH/GE miatt CH párhuzamos DE-vel. De GCH szög=GHC szög= 50 fok (mivel GC=GH) =GDE szög. EDB szög=GDE szög -ADB szög= 50-30=20 fok. A TeX-hel még nem tudok rendesen bánni, legközelebb azért megpróbálom.
|
| Előzmény: [57] Csillag, 2003-11-12 22:20:02 |
|
| [60] Hajba Károly | 2003-11-13 00:31:47 |
 Ha (46) Jenei Attila geometriai feladata a 10. és (52) Bubu kérdése a 11. akkor
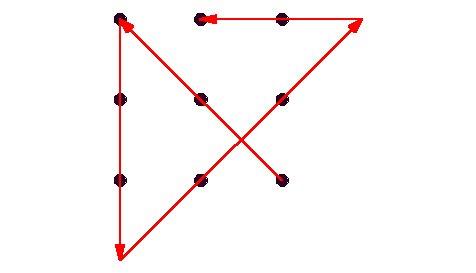
12. feladat: Kössük össze 12 darab, folytonos, a kiinduló pontba visszazáródó és a külső pontsoron túl nem nyúló egyenes szakasszal (azaz egy 12 szakaszból álló hurokkal) az alábbi 49 pontot.
HK
|
 |
|
| [59] Hajba Károly | 2003-11-13 00:09:23 |
 Kedves László!
Úgy tűnik nekem, hogy csak ketten vagyunk jelen abból a generációból, kiket elbűvölt a bűvös kocka, habár jelenleg is kapható. Ezért is ill., hogy Mihály kérésére csökkenjen a megoldatlan feladatok száma, válaszolok a bűvös kockás feladatra.
Megoldás a 9. feladatra:
Az eredeti kockán található oldaléleknek két állásuk lehetséges, alaphelyzet ill. (180°-os) elforgatottság. Nevezzük 0 ill. 1/2 spinnek. Egy rendesen összeállított kocka spinjei mindig egész számot adnak ki, tehát első ránézésre a bűvös hasáb rendellenesen lett összeállítva, ami persze nem igaz, mivel alaphelyzetből és 0 spinnel lett összekeverve.
Ha jobban megnézzük az ábrát, látható, hogy a hasáb forma miatt 4 oldalél "le lett vágva", így azoknak csak egy színűk van, de ha 180°-kal elforgatom, önmagába tér vissza. Így e 4 elemnél a 0 és 1/2 spin teljesen egyformának tűnik. Ha az összekeverés előtt egy aszimetrikus jellel meg lettek volna jelölve, akkor 1 vagy 3 elem 1/2 spin elfordulást mutatna.
Hajba Károly
|
| Előzmény: [43] lorantfy, 2003-11-08 15:50:59 |
|
| [58] lorantfy | 2003-11-12 22:31:25 |
 Kedves Lajos!
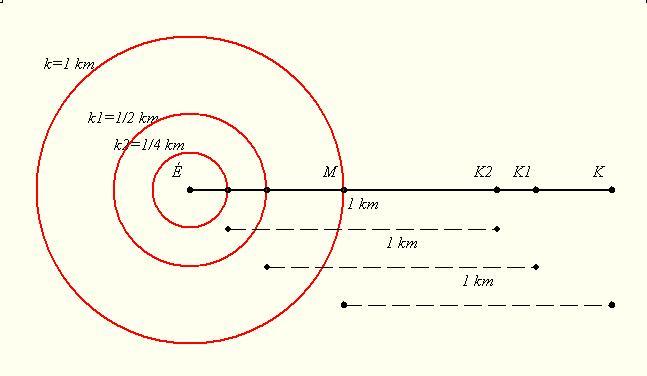
Nekem az 1 km helybenjárás kelet felé az nem tetszik, de miközben gondolatban ráhúztál a határesetre megálltál-e n-szer az 1/n sugarú köröknél és beidomítottad-e a medvét, hogy menjen körve n-szer kelet felé? Mert ha igen tiéd a Nagy Polarbear emlékérem. Persze mindig kicsit közelebbről kell elindítani a medvét. ( A felülnézeti ábrán a távolságok nem arányosak!)
Sirpinek gratula a jó ötletért!
|
 |
|
| [57] Csillag | 2003-11-12 22:20:02 |
 Üdv Mindenkinek!
Sajnos ábrát nem tudok rajzolni, de egy megoldást elmondok a geometria példához: E tükörképe a C-nél levő szögfelezőre G. A C-nél levő szögfelező és az AE metszéspontja F. GD=GF, mert
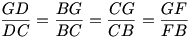
(szögfelezőtétel többszöri felhasználása, GCB =GBC =GBC =20o) =20o)
Tehát GD=GF=GE=FE(mert GEF szabályos háromszög). BGA =40,FGD =40,FGD =140,GDF =140,GDF =20,DF||CB,FDB =20,DF||CB,FDB =DBC =DBC =10,DGE =10,DGE =80,GDE =80,GDE =50,BDE =50,BDE =GDE =GDE -GDF -GDF -FDB -FDB =20. =20.
Vagyis a keresett szög 20 fokos.
GB
|
| Előzmény: [46] jenei.attila, 2003-11-10 10:44:46 |
|
| [56] Lóczi Lajos | 2003-11-12 19:38:44 |
 Tetszetős ez a megoldás... Kérdezném, kinek mi a véleménye e megoldás alábbi határesetéről: az északi sarkponttól 1 km-re délfelé kezdi meg az útját; 1 km-t északra haladva bejut az É sarkra, kelet felé onnan nem tud (mert nem lehet) haladni, tehát nem mozdul, majd dél felé 1 km-t ballag és visszajut a kezdőpontba.
Azaz, elfogadjuk-e "1 km keletre haladásnak" azt, ha valahol nem lehet kelet felé haladni.
Másik megjegyzésem: hogyan lehetne (formálisan, esetleg rajz nélkül) bizonyítani, hogy több lehetséges útvonal nincsen? (Hiszen az első megoldás is meggyőzőnek tűnt.)
Azzal is érdekes -- és minden bizonnyal sokmegoldású -- feladatokat lehetne gyártani, ha pl. a megtett távolságok összemérhetők/meghaladják a bolygó (fél)kerületét.
|
| Előzmény: [55] Sirpi, 2003-11-12 14:58:22 |
|
| [55] Sirpi | 2003-11-12 14:58:22 |
 Lorybetti: a feltételek csak úgy teljesülhetnek, ha a medve kezdetben pontosan a déli sarkponton áll, majd halad É fele, K fele és D fele és visszajut a déli sarkpontra.
Nem csak így lehet... Vegyünk az északi sarkpont közelében egy olyan szélességi kört, aminek kerülete osztja az 1km-t, és a kiindulópont ettől 1km-rel délre legyen. Ebben az esetben az É, K, D út triviálisan a kezdőpontba vezet, és akkor mégse pingvint találtunk :-) Vagyis az eredeti feladat is értelmes, nem kell permutálni az irányokat.
S
|
| Előzmény: [50] lorybetti, 2003-11-10 22:23:48 |
|
|
|
| [52] Bubu | 2003-11-12 01:14:45 |
 Rendbonto leszek, elnezest erte... Szoval a billiardgolyos feladat (amit egyebkent anno GY peldakent lekuzdottem:)) egy kulonleges matematikai kepzettseggel nem biro (erettsegi), de egyebkent feletteb intelligens rokonomat "megihlette". Azt allitja, hogy 5 meressel 12 golyobol ki tud valasztani 2 db eltero tomegut! Precizebben: van 12 kulsore egyforma golyo. 10 tomege megegyezik, kettoje elter (hogy milyen "iranyban" es mennyire, azt nem tudjuk). Egy ketkaru merleg segitsegevel valasszuk ki a ket kulonc golyot ot meressel. A megoldasrol sejtelmem sincs, de a hetvegen fogok vele foglalkozni. Aki barmilyen reszeredmenyt/otletet tud, az mailezzen legyen szives!
|
|
| [51] lorantfy | 2003-11-11 23:00:51 |
 A tevés feladat megoldása:
Az osztószámok: k , l, m, a tevék száma: n és k < l < m < n.
A végakarat teljesítésének szükséges feltétele a kölcsönkért 1 tevével:
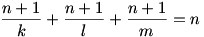
Mindkét oldalt elosztva (n+1) –el és 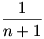 –et mindkét oldalhoz hozzáadva: –et mindkét oldalhoz hozzáadva:
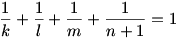
Ezt az egyenletet kell megoldanunk a 0 < k < l < m < n+1 : egész számok feltétellel.
Látszik, hogy k = 2, ugyanis k = 3 esetén a lehető legkisebb l, m, n+1 értékekre is az összeg 1-nél kisebb:
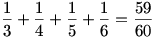
Már csak három ismeretlenünk van:
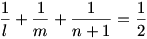
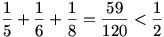
emiatt l lehetséges értékei: l = 3, l = 4
Kezdjük l = 3–mal:
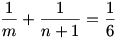
és 6 < m < 12 ( az összeg felének reciprokánál kisebb)
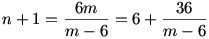
Tehát (m-6) osztója 36-nak.
m = 7, n+1 = 42, n = 41 jó megoldás,
m = 8, n+1 = 24, n = 23 jó megoldás,
m = 9, n+1 = 18, n = 17 jó megoldás,
m = 10, n+1 = 15, n = 14 NEM jó megoldás, mert 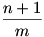 nem egész szám. nem egész szám.
l = 4 a következő eset
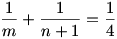
és 4 < m < 8 ( az összeg felének reciprokánál kisebb)
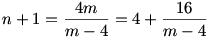
Tehát (m-4) osztója 16-nak.
m = 5, n+1 = 20, n = 19 jó megoldás,
m = 6, n+1 = 12, n = 11 jó megoldás.
Összesen 5 megoldást találtunk!
|
|
| [50] lorybetti | 2003-11-10 22:23:48 |
 Kedves Fálesz Mihály!
Egyetértek Veled, így szeretném csökkenteni a megoldatlan példák számát.A medvés példa- Fizban 22.es hozzászólása A szöveg így szólt: "Elindul Észak felé, és megy 1 km-t. Ezután elfordul Kelet felé, és megint megtesz 1 km-t. Aztán Délnek fordul, és -ki gondolta volna- megtesz még 1 km utat. Ezután a medve visszajut a P pontba."
A feladat megoldása: a feltételek csak úgy teljesülhetnek, ha a medve kezdetben pontosan a déli sarkponton áll, majd halad É fele, K fele és D fele és visszajut a déli sarkpontra. Tartok töle, hogy Fizban rosszul írta az irányokat, mert így a medve fekete-fehér színű és Pingvin névre hallgat. Ha jegesmedvéről lenne szó-ami persze fehér: az irányok sorrendje: D, K és É vagy K, É, D vagy É, D, K (utóbbi két esetben csak érinti az északi sarkpontot)
Értékes megjegyzés: A medve olyan gömbi háromszögben mozog, melynek minden szöge derékszög. Lehet hogy Bolyait is ez ihlette meg?
|
|






 =80o,
=80o,  =60o,
=60o,  =50o -- ha nem tévedek, ezekre gondoltál --, majd algebrai egyszerűsítések után a keresett
=50o -- ha nem tévedek, ezekre gondoltál --, majd algebrai egyszerűsítések után a keresett  szögre 80o adódik.
szögre 80o adódik.
 =50
=50 ADB
ADB x.
x.