| [1033] jenei.attila | 2009-11-11 13:34:10 |
 Ha képezed a a3+(a+1)3+...+(a+7)3 összeget, akkor elvégezve a köbre emeléseket és az összevonásokat, majd teljes köbre kiegészítve (számításokat nem részletezve) kapod, hogy a fenti összeg (2a+7)3+126a+441. Tehát nagyjából 2a+7 köbe. Ha a>-3,5 akkor kicsit nagyobb nála, ha a<-3.5, akkor kisebb nála. Az első esetben a kifejezésünk kisebb lesz mint (2a+8)3, ha teljesül a (2a+7)3+126a+441<(2a+8)3, vagyis két szomszédos köbszám közé fog esni, ezért nem lehet köbszám. Megoldva a fenti másodfokú egyenlőtlenséget azt kapjuk, hogy ha a<-3.49 vagy a>6.49 akkor az érték kisebb lesz mint (2a+8)3, ha viszont a>-3.5, nagyobb lesz mint (2a+7)3. Hasonlóan a másik esetben (ha a<-3.5) felírva a (2a+6)3<(2a+7)3+126a+441 egyenlőtlenséget, azt kapjuk, hogy az összeg értéke két szomszédos köbszám értéke közé esik, ha a<-13.49 vagy a>-3.51. Ezeket összevetve, és figyelembe véve hogy a egész, kapjuk, hogy -13 a a kell hogy teljesüljön, ha az összeg köbszám. kell hogy teljesüljön, ha az összeg köbszám.
|
| Előzmény: [1032] jonas, 2009-11-11 13:06:20 |
|
|
|
|
| [1029] m2mm | 2009-11-08 19:24:08 |
 Ja, tényleg elnéztem. De x=5, y=4 megoldás... 2b2+1=3k2-re visszatérve: b0=1, b1=11, bn=10bn-1-bn-2 sorozat a megoldása az egyenletnek. b0 az er. feladatnak nem megoldása, mert x0=0, de a többi jó.
|
| Előzmény: [1027] HoA, 2009-11-08 18:13:59 |
|
|
| [1027] HoA | 2009-11-08 18:13:59 |
 Talán mégis. Ugyanis az x=y=0 megoldást nem zártuk ki, mégis elveszett útközben. Nekem 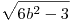 helyett helyett 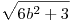 jön ki, de innen 6b2+3=c2=9k2 ;2b2+1=3k2 következik, ami b=k=1 -re még jó. 3k2-1 páros, k páratlan, k=2l+1, amiből b2=6l2+6l+1 adódik , körbeértünk. Talán elfogadva és a továbbiakból kizárva x=y=0 -t a legkisebb pozitív y-t kéne keresni, amiből kijönne, hogy csak akkor létezik, ha létezik nála kisebb pozitív l, vagyis sohasem. jön ki, de innen 6b2+3=c2=9k2 ;2b2+1=3k2 következik, ami b=k=1 -re még jó. 3k2-1 páros, k páratlan, k=2l+1, amiből b2=6l2+6l+1 adódik , körbeértünk. Talán elfogadva és a továbbiakból kizárva x=y=0 -t a legkisebb pozitív y-t kéne keresni, amiből kijönne, hogy csak akkor létezik, ha létezik nála kisebb pozitív l, vagyis sohasem.
|
| Előzmény: [1025] m2mm, 2009-11-08 15:17:00 |
|
|
|
| [1024] gabor7987 | 2009-11-08 14:47:08 |
 Ehhez a feladathoz hozzá sem tudok kezdeni. Tudna valaki segíteni?
Adjuk meg az összes olyan köbszámot, amely előáll nyolc szomszédos egész szám köbének az összegeként.
|
|



 a
a
