A KöMaL 2005. májusi matematika feladatai
Kérjük, ha még nem tetted meg, olvasd el a versenykiírást.
Feladat típusok elrejtése/megmutatása:
 |
C-jelű feladatokA beküldési határidő 2005. június 15-én LEJÁRT. |
C. 810. Melyek azok a 45-tel osztható háromjegyű számok, amelyeknek a számjegyei a felírás sorrendjében számtani sorozatot alkotnak?
(5 pont)
C. 811. Adjuk meg azokat az egymást követő egész számokat, amelyeknek az összege 100.
(5 pont)
C. 812. Megy a gőzös Kanizsára a 21 km távolságra lévő Zalakomárról. Az utat 16 perc alatt teszi meg úgy, hogy indulástól egyenletesen gyorsul, majd 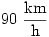 állandó sebességgel halad, végül egyenletesen lassulva megáll. Mennyi ideig megy a gőzös
állandó sebességgel halad, végül egyenletesen lassulva megáll. Mennyi ideig megy a gőzös 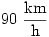 sebességgel?
sebességgel?
(5 pont)
C. 813. Egy téglalap egyik oldala 10 cm hosszú. Mekkora a téglalap másik oldala, ha egy 10 cm x1 cm-es téglalap átlósan is éppen elfér benne?
(5 pont)
C. 814. Oldjuk meg a következő egyenletrendszert, amelyben t valós paraméter:
x+y+z=t,
x+(t+1)y+z=0,
x+y-(t+1)z=2t.
(5 pont)
 |
B-jelű feladatokA beküldési határidő 2005. június 15-én LEJÁRT. |
B. 3822. Az (a;b;c) számhármassal egy lépésben a következőt lehet tenni: tetszőlegesen felcserélhetjük a számokat, vagy lecserélhetjük az (a;b;2a+2b-c) számhármasra. El lehet-e jutni ilyen lépésekkel a (2;5;13) számhármasból az (1;3;8) számhármasba?
(4 pont)
B. 3823. Legyenek x és y olyan egész számok, melyekre teljesül, hogy 4x+5y =7. Határozzuk meg 5|x|-3|y| legkisebb értékét.
(3 pont)
B. 3824. Egy tetraéder minden csúcsát tükrözzük a szemközti lap súlypontjára. Mutassuk meg, hogy a tükörképek által meghatározott tetraéder térfogata legalább négyszerese az eredeti tetraéder térfogatának.
(4 pont)
B. 3825. Az n olyan pozitív egész, amelyre 2n+1 is és 3n+1 is négyzetszám. Bizonyítsuk be, hogy n osztható 40-nel.
(4 pont)
B. 3826. Milyen négyszög az alaplapja annak a csonkagúlának, amelynek bármelyik két testátlója metszi egymást?
(4 pont)
B. 3827. Az AD szakasz érinti az ABC háromszög körülírt körét, az AC szakasz pedig az ABD háromszög körülírt körét. Mutassuk meg, hogy
AC2.BD=AD2.BC.
(4 pont)
B. 3828. Igaz-e, hogy ha egy négyszög oldalainak szorzata megegyezik a területének négyzetével, akkor a négyszögnek van legalább két derékszöge?
(4 pont)
B. 3829. Legyenek a1, a2, ..., an pozitív számok. Igazoljuk, hogy
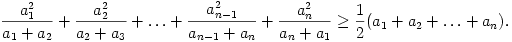
(5 pont)
B. 3830. Tekintsük az ABC háromszög AB oldalára befelé rajzolt ABDE négyzet és a BC oldalára befelé rajzolt BCGH négyzet középpontját, továbbá az AC és a DH szakaszok felezőpontját. Milyen idomot határoz meg az így kapott négy pont?
(5 pont)
B. 3831. A ,,kockás'' papíron adott egy 2005 egység oldalhosszúságú négyzet, amelynek oldalai rácsegyenesek. Rajzoljunk a négyzetbe egy olyan önmagát át nem metsző zárt töröttvonalat, amelynek minden szakasza rácsegyenes mentén halad és az összes olyan rácsponton pontosan egyszer megy át, amelyik a négyzet belsejében vagy annak határán fekszik. Mutassuk meg, hogy a töröttvonal által határolt sokszög területe nagyobb, mint a négyzet területének fele.
(5 pont)
 |
A-jelű feladatokA beküldési határidő 2005. június 15-én LEJÁRT. |
A. 374. Az x1 x2
x2 ...
... xn>0 és y1
xn>0 és y1 y2
y2 ...
... yn>0 számokra tetszőleges 0<k
yn>0 számokra tetszőleges 0<k n esetén
n esetén
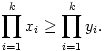
Bizonyítsuk be, hogy
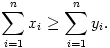
(5 pont)
A. 375. Adjuk meg az összes olyan 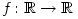 folytonos függvényt, amelyre minden
folytonos függvényt, amelyre minden 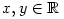 esetén
esetén
f (x+y+f(xy))=xy+f(x+y).
(5 pont)
A. 376. Az (a;b;c) számhármassal egy lépésben a következőt lehet tenni: tetszőlegesen felcserélhetjük a számokat, vagy lecserélhetjük az (a;b;2a+2b-c) számhármasra. El lehet-e jutni ilyen lépésekkel az (1;21;42) számhármasból az (5;13;42) számhármasba?
(5 pont)
A matematika gyakorlatok és feladatok megoldásait honlapunkon keresztül küldheted be:
- megszerkesztheted vagy feltöltheted az Elektronikus munkafüzetben.
(Az interneten keresztül történő beküldésről olvasd el tájékoztatónkat)

