KöMaL Problems in Mathematics, November 2008
Please read the rules of the competition.
Show/hide problems of signs:
 |
Problems with sign 'K'Deadline expired on December 10, 2008. |
K. 181. A box contains red, blue and green marbles. At least twelve marbles need to be drawn from the box to make it certain that there will be a red one among them, and at least seventeen need to be drawn to make sure that there is a red one and also a green one among them. At least seven need to be drawn to be certain that there is a marble among them that is not blue. At least how many marbles need to be drawn to make sure that at least two of them are green?
(6 pont)
solution (in Hungarian), statistics
K. 182. In a certain town, each inhabitant is either truthful or a liar, and each of them is either sane or insane. Truthful people say what they think and liars say the opposite of what they think. Sane people think what is true, and insane people think the opposite of the truth. Four inhabitants of the town said the following: Andy: I am insane. Mandy: I am truthful. Sandy: I am a liar. Dandy: I am sane. Andy: Sandy is truthful. Mandy: Dandy is insane. Sandy: Mandy is a liar. Dendi: Sandy is sane. Determine who is truthful and who is a liar, who is sane and who is insane.
(6 pont)
solution (in Hungarian), statistics
K. 183. The measures of the sides of two rectangles in centimetres are whole numbers. One of the areas is 18 cm2, and the other is 7 cm2. The difference of the perimeters is 6 cm. Find the lengths of the sides of the rectangles.
(6 pont)
solution (in Hungarian), statistics
K. 184. Sarah and Kate were solving a maths problem that involved the multiplication of two positive integers. The last digit of one of the numbers was blurred in print. Sarah thought it was an 8, and thus the result of her multiplication differed by 904 from the right answer. Kate thought it was a 3, and she got a product of . What may have been the multiplication in the problem?
(6 pont)
solution (in Hungarian), statistics
K. 185. Ten teams took part in a football championship. Every team played every other team exactly once. In each game, the winner team gets 3 points and the losers get 0. In the case of a tie, each team gets 1 point. At the end of the championship, the total of the scores of the teams was 119. Is it true that there was at least one team that tied at least four times?
(6 pont)
solution (in Hungarian), statistics
K. 186. A 11×11 cm square can be tiled with two different sets of 5 rectangles whose sides in centimetres are integers, with each length from 1 to 10 cm occurring exactly once. (Tiling means that the rectangles are not allowed to reach over the edge of the square, and they cannot even partly overlap.) Find both tilings.
(6 pont)
 |
Problems with sign 'C'Deadline expired on December 15, 2008. |
C. 960. A rectangular sheet of paper is folded along a diagonal. The four corners now form a trapezium with three sides of equal length. How long is the shorter side of the original rectangle if the longer side is 12 cm?
(5 pont)
solution (in Hungarian), statistics
C. 961. During the first half of the year, the price of gas was raised three times. The percentage increases were 5%, 6% and 10%. Experts predicted a total rise by 1/3 of the price during the whole year. If they are right, what further percentage rise is to be expected this year?
(5 pont)
solution (in Hungarian), statistics
C. 962. M is the orthocentre of the isosceles triangle ABC of base AC. Given that AC=BM, find the angles of the triangle.
(5 pont)
solution (in Hungarian), statistics
C. 963. Solve the following equation on the set of real numbers: .
(5 pont)
solution (in Hungarian), statistics
C. 964. In last year's football Champions' League, it happened for the first time ever that four teams of the same country, England (Arsenal, Chelsea, Liverpool and Manchester United), qualified for the best eight. The eight teams were paired up at random, and the winner from each pair qualified for the best four.
a) Some English football supporters wished that the English teams would not be paired together, to make it possible for all four of them to qualify for the semi-finals. What was the probability of such a pairing?
b) Other English supporters wished that the four English teams would form two pairs, to make sure that two of them would qualify for the semi-finals. What was the probability of such a pairing?
c) In reality, two English teams were paired together and the other two teams got non-English opponents. What was the probability of such a pairing?
Suggested by L. Koncz
(5 pont)
 |
Problems with sign 'B'Deadline expired on December 15, 2008. |
B. 4122. 7 fields of a 5×5 chessboard are red, and 18 fields are blue. Two of the red fields lie along the edge of the board. Line segments separating two red fields are also coloured red, and line segments separating blue fields are coloured blue. All the rest of the lines, including the edges of the board, are black. There are 35 black line segments altogether. How many red line segments are there?
(4 pont)
solution (in Hungarian), statistics
B. 4123. Find the locus of points on the plane such that the sum of squares of their distances from two given points is constant.
(3 pont)
solution (in Hungarian), statistics
B. 4124. We determine the square root of each 4-digit number, and if the result is not an integer, we round it to the nearest integer. Decide whether we have rounded up or down more numbers.
(3 pont)
solution (in Hungarian), statistics
B. 4125. Given two points in the interior of a 45o angle, construct an isosceles triangle that has its base on one arm of the angle, its apex on the other arm, and each leg passing through one of the given points.
(4 pont)
solution (in Hungarian), statistics
B. 4126. From the endpoints of a chord AB of a circle, drop perpendiculars onto a tangent drawn at a point P of the circle, different from A and B. Drop a perpendicular from P onto the chord AB. Prove that the perpendicular dropped onto the chord is the geometric mean of the perpendiculars dropped onto the tangent.
(4 pont)
solution (in Hungarian), statistics
B. 4127. Solve the equation x5-x3y2-x3y-x2y3+y2=0 on the set of integers.
Suggested by Á. Somogyi
(4 pont)
solution (in Hungarian), statistics
B. 4128. P and Q are two different points on the diagonal AC of a parallelogram ABCD. The line through P parallel to AB intersects the sides BC and AD at K and L, and the line through Q parallel to BC intersects the sides AB and CD at M and N. Show that the areas of the triangles PNM and QKL are equal.
(3 pont)
solution (in Hungarian), statistics
B. 4129. Sequence (an) is defined by the recursion a0=0, a1=1 and an=2an-1+an-2 for n>1. Prove that if , then
.
(5 pont)
solution (in Hungarian), statistics
B. 4130. Consider a finite number of line segments on a line. Prove that if they are rearranged so that the midpoints of any two line segments are moved closer to each other then the total length of the union of the line segments will not increase.
(5 pont)
solution (in Hungarian), statistics
B. 4131. A mouse is placed in one corner cell of a 3×3×3 lattice of cubes, and a piece of cheese is placed in the central cell. The mouse moves about the lattice in a random way, entering an adjacent cell in each step. In how many steps is it expected to find the cheese?
(5 pont)
 |
Problems with sign 'A'Deadline expired on December 15, 2008. |
A. 464. Let H a set and denote by P(H) the family of all subsets of H. Suppose that f and g are P(H)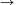 P(H) maps such that f(X)
P(H) maps such that f(X) f(Y)
f(Y) H and g(X)
H and g(X) g(Y)
g(Y) H whenever X
H whenever X Y
Y H. Prove that there exist sets A,B
H. Prove that there exist sets A,B H for which f(A)=H\B and g(B)=H\A.
H for which f(A)=H\B and g(B)=H\A.
(5 pont)
A. 465. Show that 6 does not divide for any positive integer n.
(5 pont)
A. 466. Do there exist a set of cirlces in the plane such that every line intersects at least 1, but at most 100 of them?
Miklós Schweitzer competition, 2008
(5 pont)
Upload your solutions above.
