 |
A C. 1486. feladat (2018. május) |
C. 1486. Adott az \(\displaystyle ABC\) szabályos háromszög és a \(\displaystyle k\) kör, melyeknek közös középpontja az \(\displaystyle O\) pont, területük pedig egyaránt \(\displaystyle \sqrt{\frac{\pi}{\sqrt{27}}}\). Legyenek az \(\displaystyle AO\), \(\displaystyle BO\), \(\displaystyle CO\) szakaszok meghosszabításainak a \(\displaystyle k\) körrel való metszéspontjai rendre az \(\displaystyle A'\), \(\displaystyle B'\), \(\displaystyle C'\) pontok. Adjuk meg az \(\displaystyle AC'BA'CB'\) hatszög területének pontos értékét.
(5 pont)
A beküldési határidő 2018. június 11-én LEJÁRT.
Megoldás. Használjuk az ábra jelöléseit.
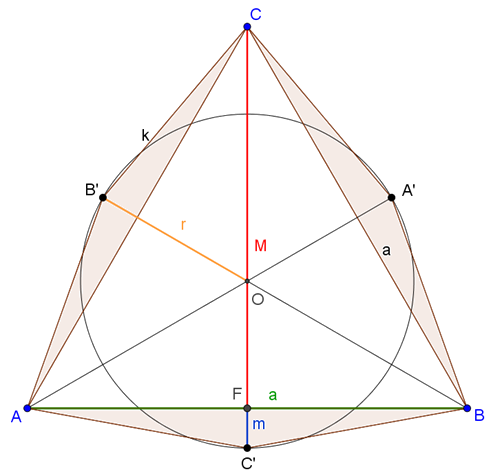
\(\displaystyle T_{kör}=T_Δ=\sqrt{\frac{π}{\sqrt{27}}}=r^2 π=\frac{a^2 \sqrt3}{4},\)
amiből
\(\displaystyle r=a\sqrt{\frac{\sqrt3}{4π}}.\)
Felhasználva, hogy \(\displaystyle M=a \frac{\sqrt3}{2}\), a felsőből
\(\displaystyle a^2=\frac{4}{\sqrt3}\cdot\sqrt{\frac{π}{\sqrt{27}}}= \sqrt{\frac{16π}{9\sqrt3}}.\)
\(\displaystyle m=r-\frac M3=a\cdot\left(\sqrt{\frac{\sqrt{3}}{4π}}-\frac{\sqrt3}{6}\right),\)
\(\displaystyle T_{ABC'}=\frac{am}{2}=\frac{a^2}{2} \left(\sqrt{\frac{\sqrt{3}}{4π}}-\frac{\sqrt3}{6}\right)=\)
\(\displaystyle =\sqrt{\frac{4π}{9\sqrt3}}\left(\sqrt{\frac{\sqrt{3}}{4π}}-\frac{\sqrt3}{6}\right)=\)
\(\displaystyle =\frac13-\frac13\frac{\sqrt{3}}{2}\sqrt{\frac{4π}{9\sqrt3}},\)
\(\displaystyle T_{ABC'}=\frac13-\frac13\sqrt{\frac{4π\cdot3}{4\cdot9\sqrt3}}=\frac13-\frac13\cdot\sqrt{\frac{π}{\sqrt{27}}},\)
\(\displaystyle T_{AB'CA'BC'}=T_Δ+3\cdot T_{ABC'}=\)
\(\displaystyle \sqrt{\frac{π}{\sqrt{27}}}+3\left(\frac13-\frac13\cdot\sqrt{\frac{π}{\sqrt{27}}}\right)=1.\)
Statisztika:
A KöMaL 2018. májusi matematika feladatai

