A C. 1729. feladat (2022. szeptember)

C. 1729. Az \(\displaystyle ABCD\) négyzet \(\displaystyle BC\) és \(\displaystyle CD\) oldalára mint átmérőre a \(\displaystyle k_1\), illetve \(\displaystyle k_2\) félköröket rajzoljuk a négyzeten kívülre. A két félkörív felezőpontja \(\displaystyle E\), illetve \(\displaystyle F\). A \(\displaystyle DE\) és \(\displaystyle AF\) szakasz felezőpontja \(\displaystyle P\), illetve \(\displaystyle Q\). Mutassuk meg, hogy \(\displaystyle P\) a négyzet \(\displaystyle AC\) átlójára, \(\displaystyle Q\) pedig a négyzet \(\displaystyle BD\) átlójára illeszkedik.

(5 pont)

A beküldési határidő 2022. október 10-én LEJÁRT.

Megoldás. Legyen \(\displaystyle DE\cap{AC}=R\), illetve \(\displaystyle AF\cap{BD}=S\). Elegendő bizonyítanunk, hogy \(\displaystyle R=P\) és \(\displaystyle S=Q\).

Az \(\displaystyle ABCD\) négyzet \(\displaystyle AC\) és \(\displaystyle BD\) átlói az \(\displaystyle M\) pontban merőlegesen metszik egymást.

A Thalész-tétel alapján \(\displaystyle BEC\sphericalangle=CFD\sphericalangle=90^{\circ}\), továbbá \(\displaystyle E, F\) felezik a megfelelő köríveket, ezért \(\displaystyle BE=CE\), valamint \(\displaystyle CF=DF\), azaz \(\displaystyle BEC\) és \(\displaystyle CFD\) egyenlő szárú derékszögű háromszögek, amelyek \(\displaystyle BC=CD\) miatt egybevágók is.

Tekintsük a következő ábrát.

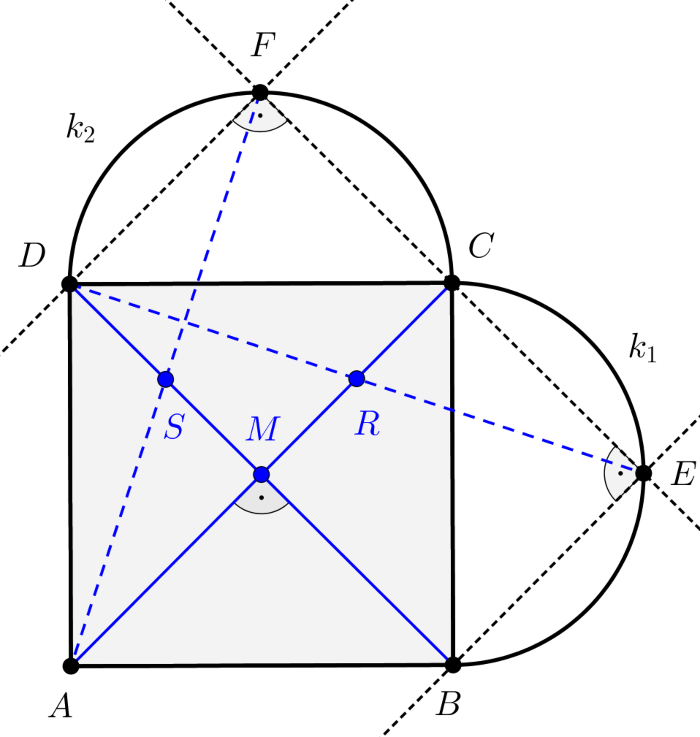
A fentiek szerint \(\displaystyle BEC\) és \(\displaystyle CFD\) egybevágó, egyenlő szárú derékszögű háromszögek, ezért \(\displaystyle EC=FC\) is igaz, továbbá \(\displaystyle ECB\sphericalangle+BCD\sphericalangle+DCF\sphericalangle=180^{\circ}\), vagyis az \(\displaystyle E, C, F\) pontok egy egyenesen vannak és \(\displaystyle C\) az \(\displaystyle EF\) szakasz felezőpontja. Az \(\displaystyle AC\) átló a négyzet \(\displaystyle BC\) és \(\displaystyle CD\) oldalaival is \(\displaystyle 45^{\circ}\)-os szöget zár be, ez az előzőek alapján azt is jelenti, hogy \(\displaystyle AC\) merőleges az \(\displaystyle EF\) szakaszra, és így \(\displaystyle RC\parallel{DF}\).

Eszerint \(\displaystyle RC\) az \(\displaystyle EFD\) háromszög középvonala, és ezért \(\displaystyle R\) a \(\displaystyle DE\) szakasz felezőpontja, tehát valóban teljesül, hogy \(\displaystyle R=P\).

Az előzőek alapján könnyen látható, hogy \(\displaystyle ACF\) derékszögű háromszög, amelynek \(\displaystyle AC\) befogóját az \(\displaystyle MS\) szakasz merőlegesen felezi, és mivel \(\displaystyle MS\parallel{CF}\), ezért \(\displaystyle MS\) az \(\displaystyle ACF\) háromszög középvonalaként felezi az \(\displaystyle AF\) szakaszt.

Így azt is beláttuk, hogy \(\displaystyle S=Q\), és ezzel a feladat állítását igazoltuk.

Statisztika:

211 dolgozat érkezett.
5 pontot kapott:	Aaishipragya Kahaly, Bánrévi Boglárka, Biborka Bernadett, Bilicki Vilmos, Dancsák Dénes, Duzmath Brigitta, Egyházi Godó, Gál András, Görömbey András István, Hajós Balázs, Hüvös Gergely, Iván Máté Domonkos, Jójárt Emese, Keszthelyi Eszter, Klement Tamás, Koós Andor, Kővágó Edit Gréta, Matyó Simon, Mészáros Anna Veronika, Molnár Kristóf, Nagy Anna Éva, Németh Hanna Júlia , Osváth Emese, Őri Zsombor, Petró Péter, Ruzsa Bence Márk, Sarkadi Sándor, Seprődi Barnabás Bendegúz, Sütő Áron, Szatmári Emese, Szittyai Anna, Tomesz László Gergő, Tóth Dániel Márk, Török Eszter Júlia, Ujpál Bálint, Varga 511 Vivien, Varga Dániel 829, Végh Eszter, Volford Barnabás, Waldhauser Miklós, Wodala Gréta Klára.
4 pontot kapott:	32 versenyző.
3 pontot kapott:	42 versenyző.
2 pontot kapott:	25 versenyző.
1 pontot kapott:	21 versenyző.
0 pontot kapott:	21 versenyző.
Nem versenyszerű:	13 dolgozat.

A KöMaL 2022. szeptemberi matematika feladatai