A P. 5419. feladat (2022. szeptember)

P. 5419. Vízszintes síkon egyenletesen, \(\displaystyle 6\) m/s nagyságú sebességgel mozgó pontszerű test gyorsulásának nagysága állandó. A test pályájának \(\displaystyle A\) és \(\displaystyle B\) pontja közé eső útja \(\displaystyle 1{,}2\)-szerese az elmozdulásvektor nagyságának. Ezt az utat a test 2 másodperc alatt teszi meg. Mekkora a gyorsulása?

Közli: Holics László, Budapest

(4 pont)

A beküldési határidő 2022. október 17-én LEJÁRT.

Megoldás. A síkbeli pályán mozgó test érintő irányú (tangenciális) gyorsulása nulla, hiszen a sebességvektor nagysága állandó. A gyorsulásvektor nagysága úgy lehet állandó, hogy az érintőre merőleges (radiális- vagy centripetális) gyorsulás nagysága is állandó:

\(\displaystyle a_\text{cp.}=\frac{v^2}{R}=\text{állandó},\)

ahol \(\displaystyle R\) a pálya görbületi sugara. Mivel a centripetális gyorsulás és a sebesség nagysága is állandó, az \(\displaystyle R\) görbületi sugárnak is állandónak kell lennie, vagyis a pályagörbe csakis kör lehet.

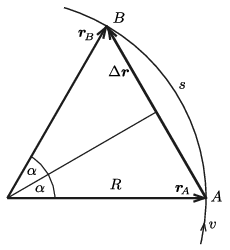
A test elmozdulása \(\displaystyle A\)-tól \(\displaystyle B\)-ig (lásd az ábrát)

\(\displaystyle \vert \Delta {\boldsymbol r}\vert=2R\sin\alpha,\)

a megtett út hossza pedig

\(\displaystyle s=2R\alpha.\)

A megadott feltétel szerint

\(\displaystyle 2R\alpha=1{,}2\cdot 2R\sin\alpha,\)

vagyis

\(\displaystyle 1{,}2\cdot \frac{\sin\alpha}{\alpha}=1.\)

Ennek a trigonometrikus egyenletnek a megoldása (amit numerikusan, próbálgatásokkal vagy számítógépes segítséggel lehet megkapni): \(\displaystyle \alpha=1{,}027\) radián.

Ha a test a \(\displaystyle 2R\alpha\) hosszú utat \(\displaystyle v\) sebességgel haladva \(\displaystyle T=2~\rm s\) alatt teszi meg, akkor

\(\displaystyle v=\frac{2R\alpha}{T},\qquad \text{vagyis}\qquad R=\frac{vT}{2\alpha}=\frac{6\cdot 2}{2\cdot 1{,}027}\,{\rm m}=5{,}84~\rm m,\)

tehát a test gyorsulásának nagysága:

\(\displaystyle a_\text{cp.}=\frac{v^2}{R}=\frac{36}{5{,}84}~\frac{\rm m}{\rm s^2}\approx 6{,}16~\frac{\rm m}{\rm s^2}.\)

Statisztika:

80 dolgozat érkezett.
4 pontot kapott:	Arnold Lőrinc, Beke Botond, Bernhardt Dávid, Bodré Zalán, Bogdán Benedek, Brezina Gergely, Bunford Luca, Chrobák Gergő, Csilling Dániel, Csiszár András, Csonka Illés, Dercsényi Bence, Elekes Dorottya, Fajszi Karsa, Fazekas Marcell, Flóring Balázs, Fórizs Borbála, Hajc Péter, Halász Henrik, Halász Sámuel, Hüvös Gergely, Juhász Júlia, Kaszonyi Márk, Klement Tamás, Kovács Barnabás, Kovács Kristóf , Lincoln Liu, Masa Barnabás, Mészáros Ádám, Molnár Kristóf, Nemeskéri Dániel, Péntek Domonkos, Petró Péter, Richlik Márton, Schmercz Blanka, Seprődi Barnabás Bendegúz, Sipeki Árpád, Szabó Márton, Szanyi Attila, Szatmári András Gábor, Támer Gergő, Vári Gergely Péter, Waldhauser Miklós.
3 pontot kapott:	Bencz Benedek, Brilli Fabiano, Farkas Dorka Hanna, Hegedűs Máté Miklós, Odrobina Zsófia.
2 pontot kapott:	4 versenyző.
1 pontot kapott:	10 versenyző.
0 pontot kapott:	10 versenyző.
Nem versenyszerű:	4 dolgozat.

A KöMaL 2022. szeptemberi fizika feladatai