A KöMaL 2018. decemberi fizika feladatai
Kérjük, ha még nem tetted meg, olvasd el a versenykiírást.
Feladat típusok elrejtése/megmutatása:
 |
M-jelű feladatokA beküldési határidő 2019. január 10-én LEJÁRT. |
M. 382. Egy vékony, hajlékony, nyújthatatlannak tekinthető fonál egyik végét egy \(\displaystyle R\) sugarú, vízszintes tengelyű, rögzített henger ,,tetejéhez'' erősítjük, a másik végére pedig egy kis méretű testet akasztunk. Egyensúlyi állapotban a fonál függőleges darabja \(\displaystyle L=3R\) hosszúságú. A testet az ábrán látható módon kitérítjük, majd magára hagyjuk. A test mozgásának periódusideje – viszonylag nagy kezdeti kitérésnél – függ az \(\displaystyle A\) ,,amplitúdótól''. Mérjük meg néhány különböző \(\displaystyle A\) esetén, hogy hány százalékkal tér el ezen inga (ún. evolvensinga) \(\displaystyle T(A)\) lengésideje az \(\displaystyle L\) hosszúságú fonálinga \(\displaystyle T_0=2\pi\sqrt{{L}/{g}}\) lengésidejétől!
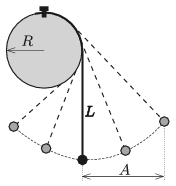
Christiaan Huygens (1629–1695) nyomán
(6 pont)
 |
G-jelű feladatokA beküldési határidő 2019. január 10-én LEJÁRT. |
G. 653. Egy reggel a mozdonyszínből két mozdony indul el ugyanabba az irányba. Az első dízelmozdony, amelynek sebessége 90 km/h, a második pedig villanymozdony, ami másfél perccel később indul 20 m/s sebességgel. A dízelmozdony 10 perccel a kifutása után találkozik a szomszédos sínen szembejövő gyorsvonattal. Mekkora a gyorsvonat sebessége, ha ezután másfél perccel találkozik a villanymozdonnyal?
(3 pont)
G. 654. Egy gyógyfürdő \(\displaystyle 12~\mathrm{m}\times20~\mathrm{m}\)-es medencéjében 75 cm magasan áll a \(\displaystyle 30\;{}^\circ\)C-os termálvíz. Ezután 1 m magasságig \(\displaystyle 50\;{}^\circ\)C-os termálvízzel töltik fel a medencét. A hőveszteségek miatt \(\displaystyle 2\;{}^\circ\)C-kal lesz alacsonyabb a medencében lévő víz hőmérséklete, mintha nem lenne veszteség a keveredéskor. Mekkora volt a hőveszteség a keveredés alatt?
(3 pont)
G. 655. Egy 27 kg tömegű, tömör téglát vízszintes asztallapra helyezünk. Ha az egyik lapjára fektetjük, 4500 Pa nyomást fejt ki az asztallapra. Egy másik lapjára fektetve 7200 Pa, a harmadik lapra fektetve pedig 2700 Pa lesz a nyomás. Mekkora a tégla sűrűsége?
(4 pont)
G. 656. Egy régi hajszárítónak két kapcsolója van. Ha az első kapcsolót zárjuk, akkor hideg levegőt fúj a hajszárító. Meleg levegővel akkor száríthatunk hajat, ha a második kapcsolót is bekapcsoljuk. Ha csak a második kapcsolót zárjuk, akkor sem a ventillátor, sem a fűtőszál nem működik. Készítsük el a hajszárító kapcsolási rajzát!
(4 pont)
 |
P-jelű feladatokA beküldési határidő 2019. január 10-én LEJÁRT. |
P. 5078. Egy jégkorongmérkőzés során nem ritka, hogy a korong sebessége eléri akár a 160 km/h-t is.
\(\displaystyle a)\) Milyen messzire csúszna egy ilyen sebességű korong a jégen, ha a korong és a jég közötti csúszási súrlódási együttható jó közelítéssel 0,1?
\(\displaystyle b)\) Mekkora átlagos erővel kell meglökni a korongot ahhoz, hogy ilyen sebességre gyorsuljon? A korong és az ütő kb. 0,01 s-ig érintkezik. A korong súlya kb. 1,5 N.
A helyi csapat csatára – büntetőlövéshez készülődve – megindul a koronggal együtt. A csatár elhatározza, hogy 5 méterről lövi be a korongot a kapuba. Tudja, hogy az ellenfél kapusának kiváló, 0,15 másodperces a reakcióideje.
\(\displaystyle c)\) Mekkora kezdősebességgel kell ellőnie a korongot, hogy az még azelőtt a kapuban legyen, hogy a kapus meg tudna mozdulni?
\(\displaystyle d)\) Mekkora erővel kell ehhez meglöknie a korongot?
Tornyai Sándor fizikaverseny, Hódmezővásárhely
(4 pont)
P. 5079. Középen átfúrt, azonos tömegű gyurmagolyók csúszhatnak egy hosszú, egyenes rúdon. Ha a rudat enyhén lejtősre állítjuk, a golyók maguktól még nem indulnak el, viszont ha elindítjuk őket, gyorsulva csúsznak lefelé. Finoman elindítva a legfelső golyót, ez eléri az alatta levőt. Ekkor összetapadnak, és együtt csúsznak tovább. Nekiütköznek a következő golyónak, ezzel is összetapadva csúsznak tovább, és így tovább. Azt tapasztaljuk, hogy mindegyik ütközés mindig ugyanakkora sebességnél következik be. Mekkora volt kezdetben az \(\displaystyle n\)-edik és az \(\displaystyle (n+1)\)-edik golyó közötti \(\displaystyle L_n\) távolság, ha az első két golyó távolsága \(\displaystyle L_1\) volt?
Közli: Fajszi Bulcsú, Budapesti Fazekas M. Gyak. Ált. Isk. és Gimn.
(5 pont)
P. 5080. Hány százalékkal nő a molekulák átlagsebessége abban a gázban, amelynek hőmérsékletét \(\displaystyle 27\;{}^\circ\)C-ról \(\displaystyle 159\;{}^\circ\)C-ra emeljük, ha a gáz
\(\displaystyle a)\) hélium;
\(\displaystyle b)\) hidrogén?
Példatári feladat nyomán
(3 pont)
P. 5081. Mekkora az ábrán látható ellenálláshálózat eredő ellenállása a \(\displaystyle C\) és \(\displaystyle D\) pontok között, ha mindegyik ellenállás \(\displaystyle R\) nagyságú? Hány százalékkal változik meg a \(\displaystyle C\) és \(\displaystyle D\) pontok közötti eredő ellenállás, ha az \(\displaystyle A\) és \(\displaystyle B\) pontok közötti ellenállást kivesszük?
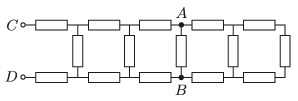
Közli: Tornyos Tivadar Eörs, Budapest
(4 pont)
P. 5082. Egy elektromosan töltött kicsiny fémgolyót \(\displaystyle \ell=1\) m hosszú, elhanyagolható tömegű szigetelőszálra függesztettünk vízszintes irányú, homogén elektromos térben. A fémgolyó egyensúlyi helyzetében a fonál \(\displaystyle {30}^\circ\)-os szöget zár be a függőlegessel. Ha az egyensúlyi helyzetéből kicsit kitérítjük a testet, mekkora az így kapott inga lengésideje?
Közli: Holics László, Budapest
(4 pont)
P. 5083. Egy lejtő hajlásszöge \(\displaystyle \alpha\), rajta a súrlódási együttható \(\displaystyle \mu\). A lejtőn lévő \(\displaystyle m\) tömegű, \(\displaystyle Q\) töltésű, kis méretű korongra mozgása közben hat egy \(\displaystyle B\) nagyságú, a lejtő síkjára merőleges irányú homogén mágneses tér is. A korongot kezdősebesség nélkül elengedjük. Határozzuk meg a korong állandósult sebességének nagyságát és irányát!
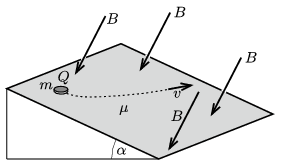
(A feladat ábrája a KöMaL nyomtatott számában fordított irányú mágneses mezővel jelent meg. Az ott vázolt mozgásirány a \(\displaystyle Q<0\) esetnek felel meg.)
A Kvant nyomán
(5 pont)
P. 5084. Hogyan változik meg egy tükörre merőlegesen beeső fény hullámhossza, ha a tükör \(\displaystyle v\) sebességgel mozog a rá eső fénnyel azonos irányban?
\(\displaystyle a)\) \(\displaystyle v=150~\frac{\mathrm{m}}{\mathrm{s}}\);
\(\displaystyle b)\) \(\displaystyle v=150\,000~\frac{\mathrm{km}}{\mathrm{s}}\).
Példatári feladat nyomán
(5 pont)
P. 5085. A mellékelt (méretarányos) ábra felső felén egy vékony, hagyományos gyűjtőlencsén áthaladó fénysugár menete látható. Hogyan fog továbbhaladni ugyanezen a lencsén az ábra alsó felén látható fénysugár?
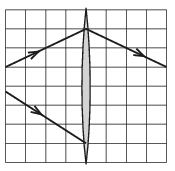
Közli: Vigh Máté, Budapest
(4 pont)
P. 5086. Mekkora energia szükséges egy oxigénatommag négy egyforma részre történő szétszakításához? Legalább mekkora energiájú neutron képes szétszakítani egy – kezdetben álló – oxigénatommagot?
Példatári feladat nyomán
(4 pont)
P. 5087. Elméletileg lehet-e szabad szemmel észrevenni egy 80 km átmérőjű krátert a Hold felszínén, ha a pupillánk átmérője 5 mm?

Csillagászati versenyfeladat
(4 pont)
P. 5088. Egy \(\displaystyle \ell\) hosszúságú fonálingát vízszintesen kitérítünk, majd elengedünk. Amikor a fonál eléri a függőleges helyzetét, egy szögbe ütközik, s innen kezdve már csak az alsó, \(\displaystyle r\) hosszúságú része lendül tovább.
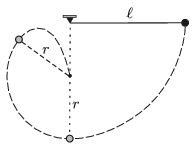
Mekkora az \(\displaystyle r/\ell\) arány, ha az ingatest, miután felfelé haladva letér valahol a körpályáról, szabadon mozogva pontosan a szögbe ütközik?
Közli: Radnai Gyula, Budapest
(6 pont)
A fizika gyakorlatok és feladatok megoldásait honlapunkon keresztül küldheted be:
- megszerkesztheted vagy feltöltheted az Elektronikus munkafüzetben.
(Az interneten keresztül történő beküldésről olvasd el tájékoztatónkat)

