A KöMaL 2022. áprilisi fizika feladatai
Kérjük, ha még nem tetted meg, olvasd el a versenykiírást.
Feladat típusok elrejtése/megmutatása:
 |
M-jelű feladatokA beküldési határidő 2022. május 16-án LEJÁRT. |
M. 413. Mérjük meg az étolaj törésmutatóját!
Közli: Gnädig Péter, Vácduka
(6 pont)
 |
G-jelű feladatokA beküldési határidő 2022. május 16-án LEJÁRT. |
G. 777. Szobahőmérsékletű presszókávét ,,felgőzöléssel'' szeretnénk felmelegíteni. Becsüljük meg, hogy mennyit romlik eközben a kávé ,,minősége'', vagyis a töménysége!
(4 pont)
G. 778. Az ábra pocsolyán áthaladó biciklikerekek vizes nyomának egy részletét mutatja a száraz aszfalton. Balról jobbra vagy jobbról balra mozgott a bicikli? Melyik az első kerekének a nyoma, és melyik a hátsóé?
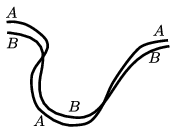
(3 pont)
G. 779. Ha a Hold felszínét óceánok és szárazulatok borítanák, akkor lenne-e a Holdon apály és dagály?
(3 pont)
G. 780. Zavarja-e a halakat, ha a parttól 2 méter távolságban beszélgetnek a horgászok? (A hang terjedési sebessége levegőben 340 m/s, vízben pedig 1500 m/s.)
(4 pont)
 |
P-jelű feladatokA beküldési határidő 2022. május 16-án LEJÁRT. |
P. 5400. A kis herceg egyik gömb alakú bolygója olyan gyorsan forog a tengelye körül, hogy az egyenlítőjén nulla a nehézségi gyorsulás. Milyen irányban nőnek a fák a bolygón?
(4 pont)
P. 5401. Egy kicsiny (pontszerűnek tekinthető), de nehéz testet két egyforma hosszú, közel azonos teherbírású fonálon tartunk. A fonalak felső végét egy vízszintes egyenes mentén lassan eltávolítjuk egymástól. Amikor a fonalak \(\displaystyle 2\alpha\) szöget zárnak be egymással, az egyik fonál elszakad, és a test a másik fonál rögzítettnek tekinthető vége körül ingaként lengeni kezd. Mekkora lehetett \(\displaystyle \alpha\), ha a másik fonál a lengések során nem szakad el?
Közli: Gnädig Péter, Vácduka
(5 pont)
P. 5402. Egy \(\displaystyle R\) sugarú, elhanyagolható tömegű, vékony hengeres abroncsra egy \(\displaystyle m\) tömegű, pontszerű nehezéket erősítettünk. Az abroncs az ábrán látható labilis egyensúlyi helyzetéből kimozdul, és akkor csúszik meg a talajon, amikor középpontjának elmozdulása éppen \(\displaystyle R\). Mekkora a tapadási súrlódási együttható az abroncs és a vízszintes talaj között?
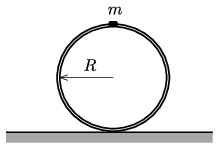
Közli: Balogh Péter, Gödöllő
(5 pont)
P. 5403. Valaki egy olyan mobilgát építését javasolta, ami egy vízszintes és hozzá \(\displaystyle 45^\circ\)-os szögben csatlakozó vaslapból áll. A két fémlapnak a közös élre merőleges mérete 1 méter, illetve \(\displaystyle \sqrt2\) méter, a fémlapok vastagsága 2 cm. ,,Ezt a szerkezetet nemcsak a vaslapok súlya, de még a víz nyomása is a talajhoz szorítja'' – érvelt a feltaláló.
\(\displaystyle a)\) Legalább mekkora (tapadási) súrlódási együtthatóra van szükség a mobilgát és a talaj között, hogy a védelem még a maximális vízmagasság esetén is biztonságos legyen?
\(\displaystyle b)\) Hol lehet az ilyen alakú mobilgátakon a talaj által kifejtett függőleges nyomóerő támadáspontja, ha 2 cm-nél vastagabb, vagy vékonyabb vaslapot alkalmazunk? Felborulhat-e a mobilgát a legmagasabb vízállásnál (vagyis amikor a víz éppen a ferde vaslap tetejéig ér)?
Vizsgáljuk meg a mobilgát elhelyezésének kétféle lehetőségét:
\(\displaystyle (i)\) a ferde felület a víz felé dől;
\(\displaystyle (ii)\) a ferde felület a védendő terület felé dől.
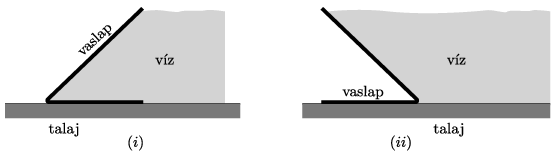
Közli: Simon Péter, Pécs
(5 pont)
P. 5404. Egy ideális Carnot-gép \(\displaystyle T_1\) és \(\displaystyle T_2\) \(\displaystyle (T_2<T_1)\) hőmérsékletű hőtartályok segítségével (izotermikus és adiabatikus állapotváltozásokon keresztül) ciklusonként \(\displaystyle W\) hasznos munkát tud végezni. Hogyan módosul a hőerőgép hatásfoka, ha a munkahenger dugattyújának kicsiny súrlódása miatt ciklusonként \(\displaystyle 2q\) hő fejlődik (\(\displaystyle q\ll W)\), és ez a hő fele-fele arányban megosztva visszakerül a hőtartályokba?
Közli: Wiedemann László, Budapest
(5 pont)
P. 5405. Két különálló ellenálláson összesen \(\displaystyle I\) erősségű áram folyik át. Igazoljuk, hogy a két ellenállásra eső összteljesítmény akkor minimális, ha a két ellenállásra eső feszültség megegyezik!
Közli: Holics László, Budapest
(4 pont)
P. 5406. Maximálisan mekkora potenciálkülönbség hozható létre egy \(\displaystyle U\) feszültségű telep és két egyforma kondenzátor segítségével? A kondenzátorok feltöltésük után szabadon átrendezhetők és újra beköthetők egy hálózatba.
Példatári feladat nyomán
(5 pont)
P. 5407. A CERN egyik lineáris gyorsítójában kezdetben állónak tekinthető protonokat gyorsítanak \(\displaystyle L=30{,}0\) m hosszú úton \(\displaystyle U=500~\)MV feszültséggel. Feltehetjük, hogy a gyorsítóban az elektromos tér homogén. Mennyi idő alatt teszik meg a protonok az \(\displaystyle L\) távolságot? (Lásd még a ,,Relativisztikus impulzus, relativisztikus mozgási energia'' c. rövid cikket honlapunkon.)
Svájci versenyfeladat
(5 pont)
P. 5408. A vízszintes felületen lévő, tartóoszloppal rendelkező, \(\displaystyle M = 3m\) tömegű kiskocsira egy fonálingát szerelünk. Az inga hossza \(\displaystyle L = 50\) cm, a végén lévő, pontszerűnek tekinthető golyó tömege \(\displaystyle m = 0{,}15\) kg. Kezdetben a testek nyugalomban vannak. Az ingát a fonál feszes állapotában vízszintes helyzetéig kitérítjük, és kezdősebesség nélkül elengedjük. A súrlódás mindenhol elhanyagolható.

\(\displaystyle a)\) Mekkora a kocsi sebessége, amikor a fonál \(\displaystyle \alpha = 60^\circ\)-os szöget zár be a függőleges iránnyal?
\(\displaystyle b)\) Mekkora erő feszíti ekkor a fonalat?
Közli: Kotek László, Pécs
(6 pont)
A fizika gyakorlatok és feladatok megoldásait honlapunkon keresztül küldheted be:
- megszerkesztheted vagy feltöltheted az Elektronikus munkafüzetben.
(Az interneten keresztül történő beküldésről olvasd el tájékoztatónkat)

