A KöMaL 2022. májusi fizika feladatai
Kérjük, ha még nem tetted meg, olvasd el a versenykiírást.
Feladat típusok elrejtése/megmutatása:
 |
M-jelű feladatokA beküldési határidő 2022. június 15-én LEJÁRT. |
M. 414. Mérjük meg a csúszási súrlódási együttható értékét több, különböző finomságú csiszolópapír és egy fahasáb között!
Közli: Vigh Máté, Biatorbágy
(6 pont)
 |
G-jelű feladatokA beküldési határidő 2022. június 15-én LEJÁRT. |
G. 781. Forraljunk vizet egy nagy lábosban a tűzhelyen. Tegyünk egy vékonyfalú pohárba csapvizet, majd merítsük a forrásban lévő vízbe úgy, hogy az sehol se érintkezzen a lábos falával. Felforr-e a pohárban a víz, ha elegendően hosszú ideig várunk?
(3 pont)
G. 782. Egy kerékpár egyenletesen, 3 m/s sebességgel halad vízszintes úton. Kerekeinek átmérője 70 cm. Ábrázoljuk a kerék különböző helyzeteiben az egyik kerületi pont sebességvektorait és gyorsulásvektorait egy-egy közös pontból indulva, azaz készítsük el a sebesség- és gyorsuláshodográfokat.
(A hodográfról rövid cikk olvasható a KöMaL honlapján itt).
Vermes Miklós feladata nyomán
(4 pont)
G. 783. Egy homogén, \(\displaystyle n\) törésmutatójú, \(\displaystyle R\) sugarú üveggömb középpontjában pontszerű fényforrás helyezkedik el. A gömböt kívülről nézzük. Hol látjuk a fényforrás képét?
(3 pont)
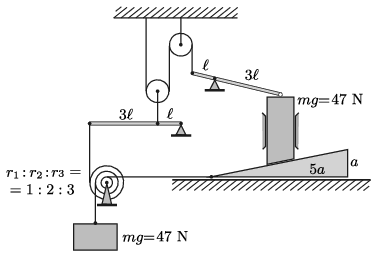
G. 784. Az alábbi ábrán egyszerű gépek kavalkádját láthatjuk. A súrlódás, valamint a csigák és emelők tömege elhanyagolható. Melyik irányba indul el a legalsó test?
(4 pont)
 |
P-jelű feladatokA beküldési határidő 2022. június 15-én LEJÁRT. |
P. 5409. Az ábrán egyszerű gépek kavalkádját láthatjuk. A súrlódás, valamint a csigák és emelők tömege elhanyagolható. Mekkora erő ébred a fonalakban?

Holics László feladata nyomán
(4 pont)
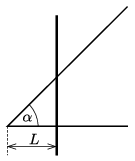
P. 5410. A vándorsólyom szárnycsapások nélkül is képes megtenni nagyobb távolságokat. Ilyenkor a mozgása két részből áll. Az első részben kiterjesztett szárnyakkal körözve emelkedik egy fölfelé áramló meleg levegőoszlopban (termikben) \(\displaystyle v_1\) függőleges sebességgel. A második részben a termiket elhagyva a vízszintessel \(\displaystyle \alpha\) szöget bezárva állandó sebességgel siklik a következő, \(\displaystyle L\) távolságra lévő termikig. A \(\displaystyle v_2\) siklási sebesség jó közelítéssel egyenesen arányos a siklás vízszintessel bezárt \(\displaystyle \alpha\) szögének szinuszával: \(\displaystyle v_2=k \sin\alpha\), ahol \(\displaystyle k\) egy ismert állandó.

\(\displaystyle a)\) Legalább milyen magasra kell a madárnak emelkednie a termikben, hogy egy emelkedésből és egy siklásból álló mozgás a legrövidebb ideig tartson?
\(\displaystyle b)\) Legalább mennyi időre van szüksége a vándorsólyomnak, hogy az egyik termik aljától eljuthasson a másik termik aljáig?
\(\displaystyle c)\) Határozzuk meg az optimális menetidejű mozgáshoz tartozó siklási szöget!
Adatok: \(\displaystyle v_1=2~\frac{\mathrm{m}}{\mathrm{s}}\), \(\displaystyle k=10~\frac{\mathrm{m}}{\mathrm{s}}\), \(\displaystyle L=2\) km.
Közli: Simon Péter, Pécs
(5 pont)
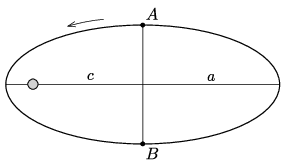
P. 5411. A Föld körül egy műhold \(\displaystyle c/a=e\) numerikus excentricitású ellipszispályán kering, keringési ideje \(\displaystyle T\). Mennyi idő alatt ér a műhold az ábrán jelölt \(\displaystyle A\) pontból a \(\displaystyle B\) pontba?
Közli: Szász Krisztián, Budapest
(4 pont)
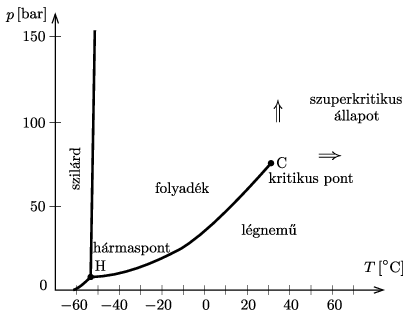
P. 5412. Ha egy gázt (állandó nyomás mellett) lehűtünk, akkor elegendően alacsony hőmérsékleten a gáz általában cseppfolyósodik (kondenzálódik, lecsapódik). Ez azonban csak bizonyos nyomástartományban történik így. Az ábra a szén-dioxid ,,fázisdiagramját'' mutatja. Legalább, illetve legfeljebb mekkora nyomás mellett történik meg a cseppfolyósodás a fenti módon? Mi történik, ha a hűtést ennél a tartománynál magasabb, illetve alacsonyabb nyomáson végezzük?
(Lásd még ,,A gőz, gáz és a kritikus hőmérséklet'' c. rövid cikket a KöMaL honlapján: https://www.komal.hu/cikkek/cikklista.h.shtml.)
Közli: Honyek Gyula, Veresegyház
(3 pont)
P. 5413. Egy 20 cm fókusztávolságú gyűjtőlencsét az ábra szerint egy domború gömbtükörre helyezünk. Mekkora legyen a tükör görbületi sugara, hogy a lencsére függőlegesen érkező, párhuzamos fénynyaláb a rendszerről való visszaverődés után is párhuzamos maradjon?
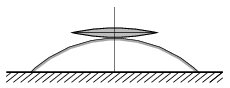
Példatári feladat nyomán
(4 pont)
P. 5414. Fémdrótból egy \(\displaystyle R\) sugarú kört formáztunk, és ugyanebből a drótból az egyik átmérőt is elkészítettük. Mekkora legyen az \(\displaystyle AB = AC\) ívek hossza, hogy az \(\displaystyle A\) és \(\displaystyle B\) pontok között mérhető eredő ellenállás megegyezzen a \(\displaystyle B\) és \(\displaystyle C\) pontok között mérhető eredő ellenállással?
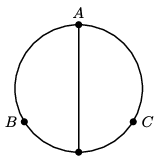
Közli: Gáspár Merse Előd, Budapest
(4 pont)
P. 5415. Egy elhanyagolható ellenállású, szigetelés nélküli huzalból, a vízszintes síkban elhelyezkedő, \(\displaystyle \alpha= 45^\circ\)-os szöget bezáró, V alakot hajlítunk. Ezt az elrendezést olyan mágneses mezőbe helyezzük, melynek \(\displaystyle \boldsymbol B\) indukcióvektora merőleges a vízszintes síkra, és nagysága a \(\displaystyle B(t) = B_0/t_0\cdot t\) összefüggés szerint változik az időben, ahol \(\displaystyle B_0\) és \(\displaystyle t_0\) ismert állandók. A V alakú vezetőre szigetelés nélküli, kezdetben rögzített fémrudat helyezünk az ábrának megfelelő módon. A rúd egységnyi hosszúságú darabjának ellenállása \(\displaystyle r\).
\(\displaystyle a)\) Mennyi hő fejlődik a fémrúdban \(\displaystyle t_0\) idő alatt?
\(\displaystyle b)\) A bekapcsolástól (\(\displaystyle t = 0\) időpillanat) számított \(\displaystyle t_0\) időpillanatban a mágneses indukció változása megszűnik. Ebben a pillanatban az eddig rögzített fémrudat a vízszintes síkban, a fémrúdra merőlegesen \(\displaystyle v_0\) sebességgel mozgatni kezdjük. Mekkora legyen ez a sebesség, hogy a rúdban folyó áram erőssége ne változzon?
\(\displaystyle c)\) Hányszor több hő fejlődik a fémrúdban a mozgatás során, mint a rögzített helyzetben, ha a fémrudat \(\displaystyle 2t_0\) hosszú ideig mozgatjuk?
Közli: Kotek László, Pécs
(5 pont)
P. 5416. Egy 1,1 nm hosszúságú, hozzá képest elhanyagolható szélességű és vastagságú térrészben öt elektron van. Ebben a térrészben a potenciális energia nulla, ezen kívül nagyon nagy. (Az elektronok egymással való kölcsönhatásától eltekinthetünk.)
\(\displaystyle a)\) Mekkora a rendszer elektronjainak gerjesztéséhez szükséges minimális energia?
\(\displaystyle b)\) Mekkora hullámhosszúságú elektromágneses hullám képes ezt a gerjesztést létrehozni? Hol a helye ennek az elektromágneses hullámnak a spektrumban?
Közli: Zsigri Ferenc, Budapest
(5 pont)
P. 5417. Vízszintes talajon álló \(\displaystyle R\) sugarú, elhanyagolható tömegű keskeny hengeres abroncs tetejére kis méretű, \(\displaystyle m\) tömegű nehezéket helyezünk (de nem erősítjük hozzá), és a rendszert a labilis egyensúlyi helyzetéből kimozdítjuk. Az egyre gyorsabban guruló abroncsról a kis test valahol lerepül.
\(\displaystyle a)\) Legalább mekkora az érintkező felületek között a tapadási súrlódási együttható, ha a mozgás során sem a kis test az abroncson, sem az abroncs a talajon nem csúszik meg?
\(\displaystyle b)\) Hol fog földet érni a lerepülő kis test?
Közli: Balogh Péter, Gödöllő
(6 pont)
A fizika gyakorlatok és feladatok megoldásait honlapunkon keresztül küldheted be:
- megszerkesztheted vagy feltöltheted az Elektronikus munkafüzetben.
(Az interneten keresztül történő beküldésről olvasd el tájékoztatónkat)

