|
|
|
|
| [1178] Lóczi Lajos | 2006-03-08 21:20:15 |
 215. feladat. A kérdés ugyanaz, mint a 214-esben, csak az integrálokat ne improprius Riemann, hanem Lebesgue értelemben értsük.
|
|
|
|
| [1175] nadorp | 2006-03-08 16:17:05 |
 b) Az 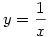 helyettesítéssel az integrál a következő alakú lesz helyettesítéssel az integrál a következő alakú lesz
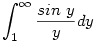 . Nyilván elég az . Nyilván elég az 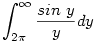 integrállal foglalkozni. Ezt a következőképpen érdemes felírni: integrállal foglalkozni. Ezt a következőképpen érdemes felírni:
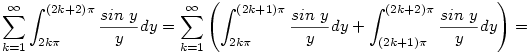
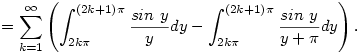
Innen már sejthető, hogy a fenti összeg becsülhető a 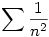 sorral, ami konvergens sorral, ami konvergens
|
| Előzmény: [1169] Lóczi Lajos, 2006-03-07 00:25:21 |
|
|
|
|
|
| [1170] jenei.attila | 2006-03-07 11:15:33 |
 Tényleg túl bonyolítod (vagy nem érted) a dolgot. Attól, hogy az együtthatók és p, q lehetnek negatívak is,ugyanúgy érvényesek Iván88 meggondolásai (van értelme negatív egészek paritásáról beszélni). Igen, negatív számok páratlan hatványa negatív, de akkor mi van? Össze tudunk adni pozitív és negatív számokat. A középső + jellel végképp nem értem mi bajod. Mennyiben más, ha a páratlan számot 2b-1 alakban írjuk fel, ugyanúgy 2b+1 alakban is megfelelő. Ne haragudj, de szerintem az ilyen hozzászólásod céltalan kötekedésnek minősíthető.
|
| Előzmény: [1168] hobbymatekos, 2006-03-07 00:02:07 |
|
| [1169] Lóczi Lajos | 2006-03-07 00:25:21 |
 214. feladat. Léteznek-e, és ha igen, végesek-e az alábbi integrálok?
a.) 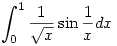
b.) 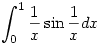
c.) 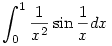
|
|
| [1168] hobbymatekos | 2006-03-07 00:02:07 |
 Csak arra gondoltam, még az nincs kihasználva, hogy p, q , és az együtthatók egész számok, azaz pozitiv és negativ számokat kellene összegezni, másrészt a negativ számok páratlan hatványai negativak, továbbá a két szumma közötti + jel az csupán a konstrukció következménye, hiszen (2b-1) alaku együtthatók is páratlan számok.
|
| Előzmény: [1167] jenei.attila, 2006-03-05 15:58:07 |
|
|
| [1166] hobbymatekos | 2006-03-04 12:40:13 |
 Szia.Szerintem: az indirekt feltevésed az volt p/q racionális és p,q relativ primek. Tehát azt kell megmutatni, hogy p/q komplex, irracionális vagy egész esetben (nem relativ primek) teljesülhet az utolsó (hibásan felirt) összeg.
|
| Előzmény: [1147] Iván88, 2005-12-31 23:50:08 |
|
| [1164] holusanyi | 2006-03-03 00:23:30 |
 Lenne egy feladat: elég érdekes szerintem, főleg mert nem tudtam megcsinálni! :) Az ötleteket e-mailben szivesen várom! 1 --> 4 --> 7 --> 9 --> 23 --> 47 --> 55 Milyen művelete(ke)t jelölnek a nyilak? Mindig ugyanaz! :)
|
|
|
|
| [1161] lorantfy | 2006-03-01 20:11:41 |
 Már másfél hónapja nem volt itt hozzászólás. Beírok egy példát, hátha érdekes lesz, azoknak akik nem ismerik:
213. feladat: A huszonhetedik dinasztia idején, amikor a repülőszőnyeg általános közlekedési eszköz volt, 7 repülőszőnyeg útvonal kötötte össze a a fővárost a birodalom többi városával. Az összes többi városból pontosan 4 repülőútvonal indult, kivéve a távoli Mesziút városát, ahonnan csak egy út indult. Mutassuk meg, hogy Messziút városából eljuthatunk a fővárosból repülőszőnyegen, esetleg más városokat érintve.
|
|
| [1160] xviktor | 2006-01-13 20:50:28 |
 Hali!
Nem olvastam el rendesen, azt hittem egesz egyutthatosrol van szo, amit irtam arra igaz. Masreszt a feladat szovege szerint van racionalis megoldas. Ha letezik, az csak a  1 lehet. 1 lehet.
Udv: Vik
|
| Előzmény: [1158] nadorp, 2006-01-13 19:33:18 |
|
|
| [1158] nadorp | 2006-01-13 19:33:18 |
 Egész együtthatósra valóban igaz, hogy ha van racionális gyök, akkor az 1 vagy -1 lehet. De a szimmetriával és azzal, hogy a -1 mindenképpen zéróhely, már baj van.
p(x)=x5+3x4+10x3-7x2-6x-1
p(1)=0, p(-1)=-10
|
|
|





 <2 esetén létezik
<2 esetén létezik




 1 lehet.
1 lehet. 