| [1385] Cckek | 2006-09-28 18:47:44 |
 Nos, a következő probléma érdekel: milyen feltételeknek kell eleget tegyen egy n-edrendű, valós elemű négyzetes A mátrix, hogy létezzen olyan X mátrix melynek a négyzete A. n=2 esetben letárgyaltam,és elég érdekes feltételeket kaptam. Érdekel, hogy foglalkozott-e már valaki ezzzel a témával, és mikor számítható ki egy mátrix n-edik 'gyöke'? Köszi
|
|
| [1384] epsilon | 2006-09-24 22:28:24 |
 Az [1369] és az utánna leírtakra visszatérve, érdekes, hogy a következő "esztétikus" dupla egyenlőtlenség "gyengébb" az összes felsoroltnál (kivéve a Wallisnál leírtat), és ez sem bizonyítható indukcióval, csak elemi "trükkel":
|
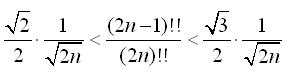 |
|
|
|
|
|
|
|
|
| [1376] Lóczi Lajos | 2006-09-24 20:21:21 |
 Igen, pont ez a tanulság. A gyengébb nem jön ki indukcióval, az erősebb igen. Ha tehát az indukcióban az "öröklődési tulajdonság" igazolása nem jár sikerrel, az még nem jelenti azt, hogy az eredeti állítás nem igaz.
|
| Előzmény: [1375] ágica, 2006-09-24 20:19:16 |
|
|
| [1374] epsilon | 2006-09-24 20:08:39 |
 Elnézést, a limesznél nem x hanem n tart a végtelenhez!
|
|
| [1373] epsilon | 2006-09-24 20:06:13 |
 Elnézést, hogy képben szúrom be, de csak a Math Typpel szoktam dolgozni!
|
 |
|
| [1372] Lóczi Lajos | 2006-09-24 20:05:36 |
 Rendben, de [1369]-et épp azért pont úgy tűztem ki, hogy direkt azt próbálja az ember indukcióval megcsinálni :) Számomra tanulságos volt, amikor találkoztam ezzel a példával.
|
| Előzmény: [1371] ágica, 2006-09-24 19:31:04 |
|
| [1371] ágica | 2006-09-24 19:31:04 |
 Ez például teljes indukcióval könnyen igazolható: n=1-re, 2-re az állítás igaz. Tegyük fel, hogy valamilyen n-re is teljesül, és vizsgáljuk n+1-re a bal oldalt:
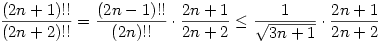
az indukciós feltevés miatt. Innen már elég belátni, hogy
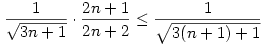
ez pedig teljesül, mivel átszorzás, négyzetre emelés és rendezés után azt kapjuk, hogy 19n 20n. 20n.
(És ebből persze következik, hogy [1369] is igaz.)
|
| Előzmény: [1369] Cckek, 2006-09-24 16:07:08 |
|
|
|
| [1368] Lóczi Lajos | 2006-09-24 10:49:54 |
 Igazoljuk, hogy tetszőleges pozitív egész n esetén fennáll, hogy

|
|
| [1367] rizsesz | 2006-09-12 19:24:27 |
 Sirpi nyert. :) Amúgy az ugyanoda nem véletlenül volt mácskákörömben, mint fel lettem világosítva. elnézést ezért a "remek" feladatért. :)
|
|
| [1366] jonas | 2006-09-12 16:54:28 |
 Egyrészt még mindig elkanyarodhatnak miután elindultak ellentétes irányba. Másrészt ennyi erővel állhatnak két futógépen egymással szemben, és mondjuk lusták, úgyhogy csak gyalogos sebességre kapcsolnak.
|
| Előzmény: [1363] rizsesz, 2006-09-11 23:55:12 |
|
|
| [1364] Suhanc | 2006-09-12 08:39:39 |
 Kedves Jonas és Rizsesz,
elnézést, nemrég figyelmeztettek rá, hogy totál nem az volt a feladat, a 3 nőnél, amit gondoltam, ill. ami szerepelt régebben. Ebben az értelemben az előző hozzászólásom nem tartalmaz fontos infót...(és nem olvastam el figyelmesen azt a 2 sort..:S)
|
| Előzmény: [1355] Suhanc, 2006-09-11 08:11:54 |
|
| [1363] rizsesz | 2006-09-11 23:55:12 |
 Nos.: Két ember elindul egy pontból ellentétes irányba "ugyanoda" jutnak 1 óra GYALOGOS séta után
hogy lehet ez?
|
|
| [1362] Doom | 2006-09-11 22:38:32 |
 Hehh... gyors vagy! Én még mindig rajzot akartam hozzá készíteni, de mivel ilyen jól leírtad, inkább leteszek róla (ugyse sikerült jól, nem jön be ez a fránya Euklidesz.. :(. )
|
| Előzmény: [1361] Suhanc, 2006-09-11 22:27:21 |
|
| [1361] Suhanc | 2006-09-11 22:27:21 |
 Tekintsük a pontok által meghatározott háromszögek közül a legnagyobb területűt, ha több ilyen van, akkor ezek egyikét. Tükrözzük a háromszöget az oldalak felezőpontjaira. Így egy olyan, 4 területű háromszöget kapunk, melynek az erdeti háromszög a középvonalakból alkotott háromszöge. Végiggondolható, hogy ezen a háromszögön kívül nem lehet pont, mert ekkor az erdetileg felvett háromszögnél nagyobb területű háromszöget találnánk... ezt a gondolatmenetet végigjárva a bizonyítást befejeztük.
|
| Előzmény: [1357] rizsesz, 2006-09-11 10:39:41 |
|






 20n.
20n. 


