| [1410] jonas | 2006-10-10 20:24:46 |
 Ezek szerint valószínűleg nem számolható könnyen, hiszen nemhogy nincs rá zárt képlet írva a Sloane-ban, hanem még "hard" flaget is kapott, tehát 9×9-es mátrixra már nem is ismert a pontos szám.
|
| Előzmény: [1409] jonas, 2006-10-10 19:57:37 |
|
| [1409] jonas | 2006-10-10 19:57:37 |
 Ez érdekes kérdés. Az ismert, hogy a q elemű test feletti reguláris n×n-es mátrixok száma (qn-q0)(qn-q1)...(qn-qn-1). Ez azért igaz, mert ha már valahogy kitöltöttük a mátrix első k oszlopát, akkor a k-adikat qn-qk módon tölthetjük ki, mert ki van zárva az a pontosan qk vektor, ami az előző oszlopok terében benne van. (Itt persze az indexek 0-tól kezdődnek.) Például q=2-re ez az A002884 sorozat.
Mármost ennek a sorozatnak a Sloane bejegyzése hivatkozik az A046747-ra, ez pedig az A055165-ra, ami valószínűleg a te kérdésedre megadja a választ.
|
| Előzmény: [1408] Cckek, 2006-10-10 05:37:42 |
|
| [1408] Cckek | 2006-10-10 05:37:42 |
 A mátrixok száma persze egyenlő az f:{1,2,...,n}x{1,2,...,n} {0,1} függvények számával ami persze 2n2 De még mindig nem tudom hány ilyen mátrix reguláris? {0,1} függvények számával ami persze 2n2 De még mindig nem tudom hány ilyen mátrix reguláris?
|
| Előzmény: [1407] Cckek, 2006-10-09 20:50:32 |
|
| [1407] Cckek | 2006-10-09 20:50:32 |
 A következő egyszerűnek tűnő problémánál akadtam el, talán valaki segít: Hány nxn-es mátrix képezhető a {0,1} halmaz elemeiből? Ezek közül hány reguláris? Minden segítséget szivesen veszek. Köszi.
|
|
|
|
| [1404] Trembeczki Diána | 2006-10-09 13:08:26 |
 Sziasztok!
Már napok óta nem tudom megoldani a következő kis feladatot, most már rákerestem, hátha valaki tud ebben segíteni! A korábbi fórumhozzászólásokat nem böngésztem végig, csak most jelentkeztem be! Szóval: A "szokásos" gyufás feladat, helyezzünk át egy gyufaszálat úgy hogy az egyenlet igaz legyen:
III - I = VI
Előre is köszönöm!
|
|
|
| [1402] rizsesz | 2006-10-08 15:45:44 |
 Egy szórakoztatóbb: hogy lehet egy 4 és egy 6 literes edény segítségével 10 liter vizet (amihez egy 10 lieters edény is van természetesen) 5-5 literre szétbontani?
|
|
|
|
| [1399] Cckek | 2006-10-07 21:04:43 |
 (k2-1)ak+1+(1-2k)ak+ak-1=(k-1)[(k+1)ak+1-ak]-[kak-ak-1]
Bevezetve a bk-1=kak-ak-1jelölést kapjuk: (k-1)bk-bk-1=0 Tehát
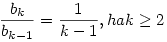
Tagonként felirva és összeszorozva kapjuk:
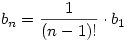
Visszatérve a jelölésre:
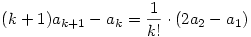
Legyen 2a2-a1=a, kapjuk, hogy (k+1)!ak+1-k!ak=a.k
Tagonként összegezve kapjuk:
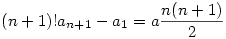
Tehát 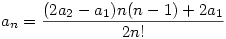
|
| Előzmény: [1398] Lóczi Lajos, 2006-10-07 20:06:04 |
|
| [1398] Lóczi Lajos | 2006-10-07 20:06:04 |
 Oldjuk meg az alábbi rekurziót ak-ra (k nemnegatív egész):
(k2-1)ak+1+(1-2k)ak+ak-1=0.
|
|
|
|
|
| [1394] rizsesz | 2006-10-03 23:39:22 |
 Gondolom ez már lepörgött: n darab rabló egy láda kincset szeretne elosztani úgy, hogy utána mindannyian úgy érezhessék, hogy nem jártak rosszul. Adjunk módszert tetszőleges n értékre (ez az n=2 esetén az egyik két részre osztja bontja a kupacot, a másik felosztja típusú).
|
|
| [1393] Cckek | 2006-10-03 22:50:48 |
 Nagyon érdekes nem?
,,...one should not expect results on iterative roots in a general situation. In fact, even roots of polynomials are not described. Even worse: we do not know whether every complex cubic polynomial has a square root..."
De azért nem hagyok még fel a témával:)
|
| Előzmény: [1391] Lóczi Lajos, 2006-10-03 22:22:25 |
|
|
|
|
| [1389] jonas | 2006-10-03 21:44:21 |
 Nos, ezt a függvényes kérdést a Knuth 2. kötet tárgyalja a hatványsoroknál. Nem tudom a részleteket fejből, úgyhogy vedd ki valahonnan a könyvet, ha érdekel.
|
| Előzmény: [1388] Cckek, 2006-10-03 21:28:00 |
|
|
|
|




 {0,1} függvények számával ami persze 2n2 De még mindig nem tudom hány ilyen mátrix reguláris?
{0,1} függvények számával ami persze 2n2 De még mindig nem tudom hány ilyen mátrix reguláris?


 R az, hogy {x}{y}
R az, hogy {x}{y} x{y}+{x}y
x{y}+{x}y