| [1616] Hajba Károly | 2006-12-14 22:25:52 |
 Ha egy színnel színezek, akkor, ha nem néztem el valamit, 20. S ebből következtetve 2 szín esetén kevesebb, mint 280, a szimmetrikus alakzatokban fellépő ismétlődések miatt. 4 szín esetén kevesebb, mint 480.
|
| Előzmény: [1615] Csimby, 2006-12-14 21:02:24 |
|
| [1615] Csimby | 2006-12-14 21:02:24 |
 301. feladat Egy 3×3-as négyzet 1×1-es kisnégyzetei közül hányféleképpen színezhetünk ki 4-et úgy, hogy a négyzet szimetriával egymásba vihető színezéseket nem tekintjük különbözőnek.
|
|
|
|
| [1612] psbalint | 2006-12-13 20:16:58 |
 http://www.asztralfeny.hu/magus/magus.php
egy kis izgalmas sziget a gyilkos feladatok végtelen óceánján... ;)
|
|
| [1611] Cckek | 2006-12-12 18:29:35 |
 Határozzuk meg az elipszis racionális kordinátájú pontjait:)
|
|
| [1610] Mhari | 2006-12-11 23:32:17 |
 Bocs, a link lemaradt: http://www.math.hmc.edu/funfacts/ffiles/20005.7.shtml
|
|
| [1609] Mhari | 2006-12-11 23:25:55 |
 Köszönöm a segítséget, különösen Lóczi Lajosnak. Életembe se jutott volna eszembe a "szőrös labda tétel" esete. De lehet, hogy még Euler sem ebben a témában. Azt hittem valami differenciálgeometriai esettel állok szemben. A link jó, ott a megoldás. Még 1x köszönöm a gyors választ!
|
| Előzmény: [1605] Lóczi Lajos, 2006-12-10 21:56:17 |
|
|
|
|
| [1605] Lóczi Lajos | 2006-12-10 21:56:17 |
 Angolul ezek a "hairy ball theorem"-ek. A válasz attól függ, hogy a mackó Euler-karakterisztikája mennyi.
Ha pl. 2, azaz folytonos deformációval átdeformálható egy gömbbe (pl. "felfújod"), akkor a tetszőleges, a felületén értelmezett folytonos vektormezőnek létezik zérushelye, azaz lesz a szőrén forgó.
Ha viszont a karakterisztika 0, tehát a maci átdeformálható egy tóruszba, akkor lehet úgy fésülni, hogy ne legyen forgója: egy szőrös úszógumit meg tudsz fésülni így.
|
| Előzmény: [1601] Mhari, 2006-12-10 10:31:21 |
|
|
| [1603] AzO | 2006-12-10 18:07:15 |
 Nalunk sundisznoval volt felteve a kerdes topologia gyakorlaton, es az a feladat ekvivalens volt azzal, hogy fujhat-e mindenhol a szel a foldgombon (a szel vektorszeru, es folytonos :) ). Erre a valasz az, hogy mindig van legalabb 1 pont, ahol nem fuj a szel. Meg hasonlo az a feladat is, hogy megkavarod a levest, es lesz olyan "pont", ami a helyen marad. Persze konnyen lehet, hogy felreertettem a feladatot :)
|
| Előzmény: [1601] Mhari, 2006-12-10 10:31:21 |
|
|
| [1601] Mhari | 2006-12-10 10:31:21 |
 Sziasztok!
Mi a valószínűsége annak, hogy úgy tudunk megfésülni egy plüssmackót, hogy ne legyen forgója? .
Állítólag létezik egzakt válasz a kérdésre, szóval nem átverés... Megj: Egy Tusnády Gábor nevű matematikust említettek, aki foglalkozik ilyesmivel. Gőzöm sincs, hogy merre induljak el.
Üdv: Mhari
|
|
| [1600] Cckek | 2006-12-09 08:00:43 |
 Ha p,q N* számítsuk ki a következő összeget: N* számítsuk ki a következő összeget:
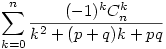
|
|
|
| [1598] jenei.attila | 2006-12-08 22:21:23 |
 Ez mintha most lett volna Arany Dániel versenyfeladat. Az eredeti egyenlet ekvivalens a következővel:
(x+y)2005=xy
, ez pedig ekvivalens a
(x-2005)(y-2005)=20052
. De 20052=524012, vagyis 9 osztója van, ezért az eredeti egyenletnek 9 megoldása van, Neked ebből csak 7 jött ki. Nem számoltam ki, ezért nem tudom melyik 2 hiányzik.
|
| Előzmény: [1597] Hajba Károly, 2006-12-08 20:20:03 |
|
|
| [1596] HoA | 2006-12-08 18:33:19 |
 Odáig igaz, hogy a nevező a számláló valamelyik részszorzata. Csak arra nem gondoltál, hogy x nem feltétlenül törzsszám - mint ahogy megoldásaidban sem az - legyen x = u * v, ezért a részszorzat olyan is lehet, hogy az 1*5*401 valamilyen s részszorzata u-val szorozva.
s*u=u*v-2005
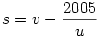
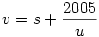
Egészekről lévén szó u is az 1*5*401 valamilyen részszorzata . Végignézve a lehetőségeket, két esetben kapunk a már ismertektől kükönböző megoldást.
s=5;u=5;v=406;x=2030;y=401*406=162806
és
s=401;u=401;v=406;x=162806;y=2030
Tehát ( 2030 ; 162806) és ( 162806; 2030 ) is két "szimmetrikus" értékpár.
|
| Előzmény: [1551] Hajba Károly, 2006-11-29 00:49:24 |
|
| [1595] jenei.attila | 2006-12-05 13:13:37 |
 Pl. "megindexeljük" az unió elemeit a [0,1]x[0,1]-beli valós számpárokkal. A pár első eleme jelenti, hogy melyik halmazból való a kiválasztott elem, a második, hogy azon belül melyik elemről van szó. A halmazok, illetve egy halmaz elemei nyilván indexelhetők [0,1]-beli valós számokkal. A [0,1]x[0,1]-beli valós számpárok halmaza pedig nyilván kontinuum számosságú, ez könnyen látható pl. a pár két számának tizedestört alakban felírt számjegyeinek összefésülésével.
|
| Előzmény: [1594] Cckek, 2006-12-04 22:00:40 |
|
| [1594] Cckek | 2006-12-04 22:00:40 |
 Ok nagyon szép. Egy direkt bizonyitást a kardinális számokkal végezhető műveletek nélkül? Tehát nem használhatjuk fel hogy k szor alef nulla az szintán alef nulla stb...
|
| Előzmény: [1593] Csimby, 2006-12-04 21:36:10 |
|
| [1593] Csimby | 2006-12-04 21:36:10 |
 Ennek c2 eleme van, hiszen c féle képpen választhatjuk meg hogy melyik halmazból veszünk elemet, és azon belül is még c elem közül választhatunk. És c2=(2A)2=22A=2A=c , ahol A jelöli alef 0-t, a természetes számok számosságát és c a kontinuum számosságot.
|
| Előzmény: [1592] Cckek, 2006-12-04 20:56:58 |
|
| [1592] Cckek | 2006-12-04 20:56:58 |
 hogyan igazoljuk hogy kontinuum sok kontinuum számosságú halmaz egyesítése kontinuum számosságú?
|
|











 N* számítsuk ki a következő összeget:
N* számítsuk ki a következő összeget: 