|
| [1842] Csimby | 2007-01-31 12:23:56 |
 307. feladat Hány rajzszög (körlap és középpontjából egy szakasz) fér el a térben?
308.feladat Amennyiben egy szállodához kontinuum sok hús vér három dimenziós ember érkezik, hogy szállásoljuk el őket, hány dimenziós ez a tér?
|
|
|
|
|
|
|
| [1836] Cckek | 2007-01-30 17:45:53 |
 Nos alkalmazva Sophie Germaine hires képletét kapjuk:
14+4.(2n)4=(22n+1-2n+1+1)(22n+1-2n+1+1) tehát a kifejezés akkor lehet prim ha az egyik tényező öt.
Így n=0 vagy n=1. De az n=0 esetben a kifejezés értéke 1.
|
| Előzmény: [1826] Lóczi Lajos, 2007-01-27 17:28:21 |
|
| [1835] HoA | 2007-01-30 13:09:49 |
 Köszönöm, megoldottam. tényleg nagyon jó. Már ha jónak lehet nevezni azt, ha látjuk, hogyan tudja egy valaki sok pénz elvételével az összes többit , minimális pénzük megtartásának reményében, egymás ellen kijátszani. :-)
|
| Előzmény: [1822] Lacczyka, 2007-01-26 21:24:37 |
|
|
|
|
|
|
|
| [1828] thukaert | 2007-01-27 18:43:24 |
 Ennek a számnak az első 12 tizedesjegye 9 -es, annak a valsége hogy valaki egy ilyet találjon tízezredrésze annak hogy ötöse legyen a lottón.Ramanujannak sikerült.Vajon hogy csinálta?
|
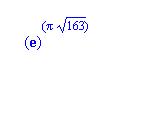 |
|
| [1827] thukaert | 2007-01-27 18:32:06 |
 A gyomos területek összkerületét vizsgáld, rá fogsz jönni, hogy ez változatlan marad , vagy csökken minden esetben amikor egy parcella elgyomosodik.
Kezdetbe az összkerület maximuma 4(n-1) Az elérni kívánt állapotban: 4n
Ez adja a feladat megoldását.
n gyomos parcella képes elgyomosítani az egészet, gondoljunk csak arra hogy keresztben vannak elhelyezve a gyomos parcellák.
Azt is elmondhatjuk, hogy n*n-n gyomos parcella esetén nem biztos hogy elgyomosodik az egész. n*n-n+1 esetén biztos .Ennek átgondolása némi időt igényel
|
| Előzmény: [1824] lorantfy, 2007-01-27 10:57:59 |
|
| [1826] Lóczi Lajos | 2007-01-27 17:28:21 |
 306. feladat. Adjuk meg azokat az n pozitív egészeket, amelyre 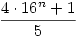 prímszám. prímszám.
|
|
|
| [1824] lorantfy | 2007-01-27 10:57:59 |
 Jó lenne újra számozni a feladatokat! Talán a 304. volt az utolsó számozott. Egy érettségi feladatsorban találtam az alábbi példát:
305. feladat: Egy négyzet alakú földterület n x n kisebb négyzetre van felosztva. Ha egy területrésznek legalább két szomszédja gazos, akkor ez a terület is elgazosodik.
Lássuk be, hogy n db gazos területrész elgazosíthatja az egész táblát, de n-1 db gazos területrész semmiképpen sem.
A feladat bármely általánosítása, továbbfejlesztése vagy hasonló feladat érdekelne. Ha valakinek eszébe jut ilyen, akkor legyenszíves nekem emilben elküldeni. Előre is köszönöm!
|
|
| [1822] Lacczyka | 2007-01-26 21:24:37 |
 Igazad van.. tényleg kimaradt... nem vagyok még gyakorlott TeX -használó, és az 50 százaléknál százalékjelet használtam, és így egy csomó minden kimaradt. Mindenesetre bocsánat a hibáért, itt a feladat:
Van 10 kalózunk, akik szereztek száz aranyat, és egy sajátos osztozkodási eljárással osztják szét. Sorba állítják magukat elvetemültség alapján, és a legelvetemültebb kalóz tesz egy osztozkodási ajánlatot: megmondja, hogy ki mennyit kap a 100 aranyból. Ezek után a kalózok szavaznak, és ha megvan az 50 százalék, akkor elfogadtatik a javaslat, ha nincs meg, akkor a kalózt vízbe dobják, és a második legelvetemültebb tehet ajánlatot, és így tovább. A szavazásnál annak a kalóznak a szavazata is számít, aki a javaslatot tette. A kalózok döntési elvei: 1)leginkább életben akarnak maradni. 2) pénzéhesek, vagyis úgy döntenek, ahogy több arany üti a markukat. 3) vérszomjasak: ha nem származik hátrányuk egy társuk halálából, akkor automatikusan nem szavazzák meg a javaslatát. Kérdés: hány aranyat tud megtartani magának a legelvetemültebb rabló? Egyáltalán, életben maradhat? A feladat megítélésem szerint nagyon jó... ha nem ismerted, akkor határozottan ajánlom figyelmedbe :)
|
| Előzmény: [1819] jonas, 2007-01-26 20:58:40 |
|
| [1821] tomii282 | 2007-01-26 21:09:40 |
 akk hogy is van ez a kalozos pelda?
|
|
| [1820] S.Ákos | 2007-01-26 21:05:42 |
 Legyen adott egy egységsugarú k1 kör a síkban. Hol van azon pontok mértani helye a síkban, amelyekből adott r sugárral rajzolt körnek és k1-nek a közös része éppen k1 területének a fele? 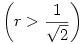
|
|
|
| [1818] tomii282 | 2007-01-26 20:38:19 |
 a kalozos feladatot h kell megoldani?
|
|