|
| [1867] Mhari | 2007-02-04 20:28:38 |
 Sziasztok! ...hát gyerekek, én csak ámulok és bámulok a sok rajzszög láttán, de nekem sokkal prózaibb gondom van már megint. Ahogy elnézlek benneteket, az én problémám nem is probléma (csak nekem). Szóval a probléma: 3*x*x+4*x*y+y*y=p Ahol x,y egészek, p pedig prím szám. Mi a megoldás?
Van ennek egy édestestvére, x*y*y+2*x*y+x-243*y=0 ahol x,y pozitív természetes szám, de azt simán meg lehet oldani, nehézség nélkül.(Még nekem is sikerült!)
De az elsővel sehogyan sem boldogulok. Próbáltam megoldani, mint felületet, még ábrázoltam is a Derive-val, jól is nézett ki, de nem sokra mentem vele. (Megjegyzem tudom a megoldást, 4 pár van belőle, de megoldani nem tudom.) Ha valaki tud, segítsen megoldani!
Üdv: Attila
|
|
| [1866] jonas | 2007-02-02 15:02:52 |
 Pontosan.
Továbbá az olcsóbb rajzszögeknél a tűt a fej lemezéből vágják ki és hajlítják ki, tehát ilyenkor a körlapból hiányzik egy szakasz, ami ugyanonnan indul, mint ahonnan a tű. Ilyen rajzszögekből is elfér kontinuum sok.
|
| Előzmény: [1865] Sirpi, 2007-02-02 13:36:53 |
|
| [1865] Sirpi | 2007-02-02 13:36:53 |
 Ha a tű nem indulhat kerületi pontból, akkor ez nem jelent általánosítást, hiszen minden rajzszög feje nyeshető úgy, hogy a tű a középpontból induljon.
Ha meg indulhat kerületi pontból (de továbbra sem lehet a fej síkjában), akkor simán el lehet kontinuum sokat helyezni.
|
| Előzmény: [1864] Csimby, 2007-02-02 10:38:55 |
|
| [1864] Csimby | 2007-02-02 10:38:55 |
 A hétvégén áttanulmányozom amiket írtál, csak most vizsgáztam és nem volt rá időm. Amúgy még egy általánosítási lehetőség, ha a tű nem a fej középpontjából indul.
|
| Előzmény: [1863] jonas, 2007-02-01 21:22:08 |
|
|
| [1862] jonas | 2007-02-01 21:16:38 |
 Ha ez működik így, akkor a gombás vagy T betűs ennek speciális esete. Sőt, a szállodásnak is, hiszen minden ember lenyelhet egy rajzszöget. Csak a nyolcasos feladatra nem ad semmit.
|
| Előzmény: [1861] jonas, 2007-02-01 21:11:53 |
|
| [1861] jonas | 2007-02-01 21:11:53 |
 Még egy ábra a bizonyítás második feléhez: a kék vonal (valójában gúla) fölé nem nyúlhat másik rajzszög, ezért ahol a kék és a piros vonal metszi egymást, a fölé nem érhet az adott rajzszög alatti másik rajzszög közepe.
(Megjegyzem, nem feltétlenül van egy rajzszög alatti következő rajzszög, a rajzszögek fölfele torlódhatnak.)
|
 |
| Előzmény: [1860] jonas, 2007-02-01 21:02:26 |
|
| [1860] jonas | 2007-02-01 21:02:26 |
 Akkor most a változatosság kedvéért én próbálok meg egy bizonyítást a rajzszögesre (307. feladat).
Azt látom be, hogy megszámlálható soknál nem lehet több rajzszög. Tegyük fel ennek ellenkezőjét.
Először vegyünk egy olyan egyenes irányt, amivel megszámlálhatónál több rajzszög feje nem párhuzamos. Ilyen irány biztosan van: három páronként merőleges irány közül legalább az egyik biztosan ilyen.
Irányítsuk az összes fejet a szerint, hogy a kiválasztott irány mindegyiknek ugyanarra az oldalára mutasson. Két részre oszthatjuk a rajzszögeket a szerint, hogy a fejnek az előbbi irányítás szerint melyik oldalára áll ki a tűje. Vegyük a kettő közül csak a nagyobb csoportot.
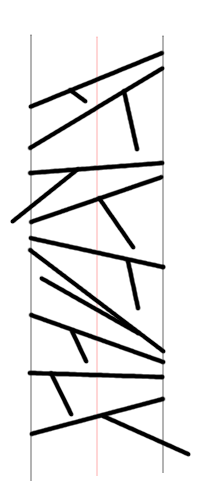
Most vetítsük a rajzszögek fejét a kiválasztott irányban egy merőleges síkra -- kivéve azokat a rajzszögeket, amik párhuzamosak az iránnyal, tehát a vetületük lapos lenne. Vegyünk a síkon egy koordináta-rendszert, és vágjuk le az összes fejet olyan paralelogrammává, aminek ez a vetülete egy racionális koordinátájú téglalap, de azért a tű továbbra is a fej belsejéből induljon ki. Ilyen racionális koordinátájú vetületből csak megszámlálható sok van, tehát van megszámlálhatónál több olyan fej, aminek azonos a vetülete. (Lásd az ábrát.)
Vágjuk még le a rajzszögek tűit úgy, hogy ne lógjon ki a vetületük a fejek vetületéből.
Mármost nézzük a fejek közepét (ahol a piros egyenes metszi őket). Könnyen látható, hogy ha van egy rajzszögünk, akkor ehhez a tű irányában nem lehet akármilyen közel másik rajzszög, mert az nem metszheti sem a tűt, sem a fejet. Valójában ha a tű vége a vetítés irányában bizonyos távolságra van a fejtől, akkor a fej közepe a következő rajzszögek közepétől legalább fele ekkora távolságra van.
Ezért aztán mindegyik rajzszög közepétől a tűk irányában van egy pozitív hosszúságú szakasz, amin nincs másik rajzszög közepe. Ezen a szakaszon vehetünk egy racionális pontot, ezek mind különböznek, tehát csak megszámlálhatóan sok rajzszögünk lehet.
|
 |
| Előzmény: [1842] Csimby, 2007-01-31 12:23:56 |
|
|
| [1858] Lóczi Lajos | 2007-01-31 19:27:30 |
 Ha nem mértékelmélettel fogalakozó könyvet nézel, a Baire-tétel nem a végén lesz. A "Baire category theorem"-re rákeresve meg a neten a bizonyítást is könnyűszerrel felleled.
|
| Előzmény: [1854] jonas, 2007-01-31 15:08:11 |
|
| [1857] HoA | 2007-01-31 16:38:22 |
 Azt hiszem jó nyomon járok, ezek nálam is speciális esetek: Hogyan lehet egy biztos halálraitélt szavazatával éppen megúszni?
Ha a kalózhajót egy olyan rendszernek tekintjük, melynek állapotait a kalózok száma szerint A1,A2,..- vel jelöljük, akkor A2-től A204-ig bezárólag A203 az egyetlen instabil állapot: az ajánlattevőt vízbe dobják és A202 lép életbe. Jelöljük a kalózokat a sor végéről számolva K1,K2,...-vel. A204 azért is érdekes állapot, mert itt először nem egyértelmű, ki kap az aranyból. K204 számára az A202-es állapot 102 vesztese közül bármelyik 100 megfelel. Ezekkel, valamint a saját és a halálraítélt K203 szavazatával megvan az 50%-a. A kisebb indexű állapotokban mindig a megelőző állapot veszteseinek kellett adni, hiszen ha valaki csak ugyanannyit kap , mint a kalóz vízbedobása esetén biztosan, akkor a 3) szabály szerint ellenszavazóvá válik. Ha a szabályok pontosak, ez szerintem azt eredményezi, hogy a következő stabil állapotban (A208) - és a nagyobb indexűekben is - az osztó saját magán (K208) és a három "halálraítélten" (K205,K206,K207) kívül bármelyik 100-nak adhat 1-1 aranyat, hiszen A202 nyertesei ( = A204 biztos vesztesei ) valamint K203 és K204 biztosan jobban járnak vele, mint A204-ben; ha pedig A202 egyik vesztese kap, nem lép be a 3) szabály, hiszen ő nem lehet biztos benne, hogy K204 adna-e neki, a biztos esemény áll szemben egy kb. 98%-os valószínűséggel.
Itt abba is hagyom. Nyilván a feladatot már kielemezték, csak azt jelezd, ha valahol tévedek.
|
| Előzmény: [1840] Lacczyka, 2007-01-30 21:50:22 |
|
|
| [1855] Sirpi | 2007-01-31 15:25:56 |
 Hú, efölött valahogy elsiklottam, szemléletesen bennem egy egyenes rajzszög képe volt, és így hirtelen nem is látom, hogyan javítható a megoldásom. Mert akármennyire el lehet görbíteni. Ráadásul ezek a rajzszögek nem javíthatók úgy, mint az egyenesek, hogy nyesek belőlük, és akkor már csak megszámlálhatóan sok lehet, mert a kör és a szakasz szöge kontinuum értéket felvehet.
|
| Előzmény: [1853] jonas, 2007-01-31 15:05:14 |
|
| [1854] jonas | 2007-01-31 15:08:11 |
 A tétel a Baire-féle kategóriatétel volt, a könyv a Járai: Mértékelmélet, az okos ember Garay tanár úr, a verseny pedig, azt hiszem, a BME matematikaverseny két évvel ezelőtt.
A feladat és az állítás már nagyobb gond. Megpróbálok utánanézni.
|
| Előzmény: [1850] Csimby, 2007-01-31 14:25:51 |
|
| [1853] jonas | 2007-01-31 15:05:14 |
 Ügyes megoldás. Nem is gondoltam rá, hogy a különböző méretűeket külön vagyük.
Persze úgy, ahogy leírod, csak akkor működik, ha a rajzszögek tűje merőlegesen áll a fejére. Nézd:
|
 |
| Előzmény: [1851] Sirpi, 2007-01-31 14:41:18 |
|
|
| [1851] Sirpi | 2007-01-31 14:41:18 |
 Akkor a rajzszögesre belátom, hogy csak megszámlálható sokat lehet. Tegyük fel, hogy van egy olyan kitöltés, ahol a rajzszögek száma több, mint megszámlálható. Ekkor minden rajzszöget "nyessünk" meg. Vegyük a szár hosszát (l), és a kör sugarát (r), és mindkettőt csökkentsük le 1/n-re, ahol n egész. Ekkor továbbra is jó kitöltést kapunk.
Ezek után elég belátni, hogy minden n-re, ezekből az r=1/n, l=1/n méretű rajzszögekből csak megszámlálható sok fér el, ekkor az összes n-re együttesen is.
Ezt elég n=1-re belátni, a többi n-re csak hasonlóságot kell alkalmaznunk. Vegyük minden rajzszögön a szárnak a körhöz csatlakozó végpontjához közelebbi mondjuk 10-edelőpontját, és rajzoljunk köré 1/10 sugarú gömböt. Nem megyek bele a technikai részletekbe, de "szemléletesen látszik", hogy ezek a gömbök diszjunktak, aki akarja, beláthatja egzaktul. Mindben van rac. pont, így készen vagyunk.
|
| Előzmény: [1842] Csimby, 2007-01-31 12:23:56 |
|
|
| [1849] jonas | 2007-01-31 14:23:22 |
 Hát, a könnyűeket még a gimnáziumban tanultam Tünde nénitől.
A nehéz akkor merült fel, amikor egy versenyen beadtam egy feladatra egy félig jó megoldást, aminek a végén kijött az, hogy az állítás teljesül ha ez és ez a számosságos állítás igaz. Ez a megoldás (mivel csak egyirányú implikáció jött ki) csak akkor ér pontot, ha az a számosságos dolog tényleg igaz, ezért utólag megkérdeztem okos embereket, hogy igaz-e.
|
| Előzmény: [1848] Csimby, 2007-01-31 14:20:44 |
|
|
| [1847] jonas | 2007-01-31 14:15:33 |
 Ilyen számosságos feladatokból találkoztam már olyannal is, aminek a megoldását nem is értettem meg, mert valami tételt használt, ami csak a tankönyvek leghátában van benne, és ott is bizonyítás nélkül.
|
|
|
| [1845] jonas | 2007-01-31 13:39:06 |
 Aki akar gondolkozni a szállodás feladaton, az ne olvassa el ezt.
Az emberesre valami olyasmi volt a megoldás, hogy veszünk miden ember belsejében egy racionális koordinátájú pontot, és mivel ilyenből csak megszámlálható sok van.
Ilyen pont létezését persze csak akkor könnyű garantálni, ha az emberek tisztességes alakúak, mondjuk Borel-halmazok.
|
| Előzmény: [1844] Csimby, 2007-01-31 13:33:49 |
|
|










