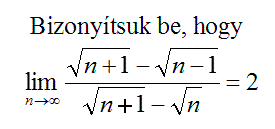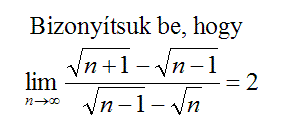|
| [1956] Cckek | 2007-03-31 20:27:37 |
 Bizonyítsuk be, hogy ha egy gyűrűben az 1-(xy)2 elem invertálható, akkor 1-(yx)2 is invertálható.
|
|
|
|
| [1955] Cckek | 2007-03-29 20:11:02 |
 Hány számjegye van 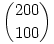 -nak? -nak?
|
|
|
|
|
| [1949] Cckek | 2007-03-27 10:19:18 |
 Bizonyítsuk be, hogy az (R,+) és (C,+) csoportok izomorfak.
|
|
| [1948] Lóczi Lajos | 2007-03-24 21:55:34 |
 Deriváljuk az integrált az x paraméter szerint, majd használjuk a jól ismert 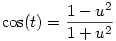 helyettesítést, ahol u=tan (t/2). Ekkor az u változó szerint egy racionális törtfüggvényt kapunk, aminek van elemi primitív függvénye. Visszahelyettesítve a t változót az alábbit kapjuk: helyettesítést, ahol u=tan (t/2). Ekkor az u változó szerint egy racionális törtfüggvényt kapunk, aminek van elemi primitív függvénye. Visszahelyettesítve a t változót az alábbit kapjuk:
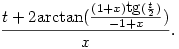
Ennek a megváltozása kell t=0 és t= között. A függvény t=0-ban 0, a t között. A függvény t=0-ban 0, a t  - határesetben pedig x-től függően kétféle értéket vesz fel: vagy nullát vagy 2 - határesetben pedig x-től függően kétféle értéket vesz fel: vagy nullát vagy 2 /x-et. Már csak x szerint kell a primitív függvényt visszakeresni, ami persze triviális. (Az x=0, x=1, x=-1 eseteket persze külön meg kell vizsgálni az eredeti határozott integrálban.) /x-et. Már csak x szerint kell a primitív függvényt visszakeresni, ami persze triviális. (Az x=0, x=1, x=-1 eseteket persze külön meg kell vizsgálni az eredeti határozott integrálban.)
Végeredmény: az eredeti integrál értéke 0, ha -1 x x 1, míg 2 1, míg 2 log |x|, ha x>1 vagy x<-1. log |x|, ha x>1 vagy x<-1.
|
| Előzmény: [1947] Cckek, 2007-03-24 19:44:40 |
|
| [1947] Cckek | 2007-03-24 19:44:40 |
 312.feladat Ha már integráloknál tartunk:
Számítsuk ki a következő integrált:
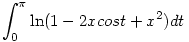
|
|
|
| [1945] Lóczi Lajos | 2007-03-20 03:00:23 |
 311. feladat. Mekkora a tangensfüggvény négyzetgyökének görbe alatti területe 0 és  /4 között? /4 között?
|
|
|
| [1943] Csimby | 2007-03-11 13:39:10 |
 309.feladat Van e olyan valós szám amelynek bármely egész számrendszerben felírt alakjában minden számjegy szerepel legalább egyszer.
310.feladat Igaz-e, hogy additív halmazfüggvények szorzata is additív?
Amúgy nincs kedvetek visszatérni a feladatok sorszámozásához? Szerintem az olyan jól bejött eddig...
|
|
|
| [1941] Lóczi Lajos | 2007-03-10 18:10:09 |
 Elképzelhető, hogy mi nem tudjuk megoldani a feladatot, mert nehéz; azért írtam be csak, mert meglepően egyszerű s szép a végeredménye. Inkább sejtsük meg numerikusan, vagy keressük meg az interneten az értékét, illetve, hogy ki az, aki rátalált erre a formulára. (Bár azt is el tudom képzelni, hogy igazából nem is számít, hogy pontosan prímekről van benne szó, és esetleg elég lenne egy alsó/felső becslés az n-edik prímszámra, és abból is ugyanaz az érték jönne ki?)
|
| Előzmény: [1940] Cckek, 2007-03-10 17:25:37 |
|
|
| [1939] Lóczi Lajos | 2007-03-09 23:53:09 |
 Jelölje pn az n-edik prímszámot.
Határozzuk meg a 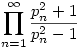 végtelen szorzat értékét. végtelen szorzat értékét.
|
|
|
|
|
|
|
| [1933] Doom | 2007-03-06 07:29:59 |
 Legutóbb rossz helyre tettem, remélem itt már jó...
Egy 'a' oldalú szabályos háromszög minden csúcsában 1-1 kutya áll (A, B és C), majd egyszerre elkezdenek futni egymás felé azonos sebességgel: A B felé, B C felé és C pedig A irányában. Mennyi idő múlva találkoznak?
Segítségként egy "sejtés": egy furcsa "spirál-alakot" megtéve a háromszög középpontjában fognak találkozni, mégpedig egyszerre.
|
|






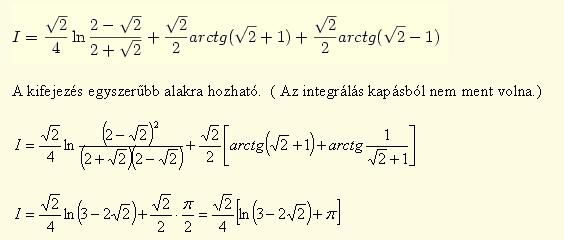
 között. A függvény t=0-ban 0, a t
között. A függvény t=0-ban 0, a t
 x
x