| [2269] Csimby | 2007-09-12 22:29:10 |
 Szia!
Lehet, hogy nem jól értem a feladatot, de pl., ha n=3 és az egyenesek a következőek: (z=0,x=0); (z=0,x=1); 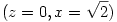 , akkor véges sok egyenessel nem lehet megoldani, hiszen ha az egyenlőközű párhuzamosok távolsága: L, akkor egyrészt 1=kL másrészt , akkor véges sok egyenessel nem lehet megoldani, hiszen ha az egyenlőközű párhuzamosok távolsága: L, akkor egyrészt 1=kL másrészt 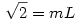 ahol n és m poz. egész, tehát L egyrészt rac. másrészt irrac. kell, hogy legyen. Meg azt sem értem, hogy mit jelent az, hogy egyenlőközű ha az egyenesek nem esnek egy síkba, csak mert 3-nál több párhuzamost nem tudsz úgy elhelyezni a térben, hogy bármely 2 ugyanakkora távolságra legyen egymástól. (Síkban gondolom azt jelenti, hogy egymás után mindig ugyanakkora távolságra következnek, de térben mi a sorrend?) ahol n és m poz. egész, tehát L egyrészt rac. másrészt irrac. kell, hogy legyen. Meg azt sem értem, hogy mit jelent az, hogy egyenlőközű ha az egyenesek nem esnek egy síkba, csak mert 3-nál több párhuzamost nem tudsz úgy elhelyezni a térben, hogy bármely 2 ugyanakkora távolságra legyen egymástól. (Síkban gondolom azt jelenti, hogy egymás után mindig ugyanakkora távolságra következnek, de térben mi a sorrend?)
|
| Előzmény: [2266] Cckek, 2007-09-10 22:53:29 |
|
| [2268] rizsesz | 2007-09-12 19:57:31 |
 a skatulya-elv alapján minden helyiértékhez létezik legalább 2 olyan szám a 11 közül, amelyekre igaz, hogy az adott helyiértéken ugyanaz a szám áll. mivel végtelen sok helyiérték van, és a 11 szám közül véges sokféleképpen lehet kettőt kiválasztani (55 módon), ezért ha bármelyik 2 számhoz hozzárendeljük az egyező helyiértékek számát, akkor ezek egyinkének végtelennek kell lennie, lévén az összes egyezések száma végtelen.
|
|
| [2267] Lbandi | 2007-09-12 19:47:24 |
 Bizonyítsuk be, hogy az 1pi, 2pi, 3pi ... , 11pi számok között van két olyan, mely végtelen sok számjegyben megegyezik.
|
|
| [2266] Cckek | 2007-09-10 22:53:29 |
 Nagyon sajnálom ezt a feladatom itt kitűzni, ám legyen:) Adott n darab nemegyenlőközű párhuzamos (nyaláb) a térben. Legkevesebb hány párhuzamost (m darab, m=f(n)) kell húzni hozzájuk, hogy egyenlőközű párhuzamosokat (nyalábot) kapjunk?
|
|
| [2265] Cckek | 2007-09-05 16:08:11 |
 Ez azt hiszem valós elemű mátrix esetén is igaz amennyiben az diagonizálható, az-az n darab különböző sajátértékkel rendelkezik. Legalábbis ezt a Jordan féle kanonikus alakból be tudom bizonyítani. A legnagyobb probléma akkor van ha vannak többszörös sajátértékek. Jó úton haladok???
|
| Előzmény: [2254] ilozagrav, 2007-08-26 21:30:33 |
|
|
|
|
|
| [2260] Yegreg | 2007-09-04 18:20:14 |
 Szerintem a legelegánsabb megoldás pl. a X+XXX X :oD X :oD
Ha megengedjük a "ferde" egyest, akkor -XI+XXI=X. Jobb ötletem most nincs.
|
|
| [2259] parizsi | 2007-09-04 17:59:51 |
 szeretném a nagyérdemű segítségét kérni az alábbi feladat megoldásához:XI + XXX = X egy gyufaszálat lehet elmozdítani a feladat megoldásához.
|
|
| [2258] Doom | 2007-09-03 16:40:54 |
 3 kitérő él: semelyik 2 nem metsző és semelyik 2 nem párhuzamos (pl. az egy csúcsból induló 3 él NEM kitérő, pedig különböző irányúak).
|
| Előzmény: [2256] HoA, 2007-09-03 15:25:28 |
|
| [2257] rizsesz | 2007-09-03 16:40:14 |
 a., a 3 kitérő él azt jelenti, hogy 3 közös ponttal nem rendelkező élre gondolok. ha a hagyományos kockavázat nézzük, akkor egy él alulról, egy oldalsó él és egy felülről, úgy, hogy semelyik két élhez nem tartozik közös csúcs; forgatással és tükrözéssel egybevágóság erejéig egy ilyen élhármas létezik.
b., igazából véges henger, olyan értelemben, hogy megoldást a kocka síkjában keresünk.
|
| Előzmény: [2256] HoA, 2007-09-03 15:25:28 |
|
| [2256] HoA | 2007-09-03 15:25:28 |
 Kérdések:
a) a 3 kitérő él úgy értendő, hogy 3 különböző irányú? b) egy éltől adott távolságra lévő pontok halmaza végtelen henger vagy két félgömbbel lezárt véges henger?
|
| Előzmény: [2255] rizsesz, 2007-09-02 20:52:05 |
|
| [2255] rizsesz | 2007-09-02 20:52:05 |
 Helló! Nem tudom, hogy hanyadik feladat sajna, de itt a szöveg:
Egy kocka 3 kitérő élétől egyenlő távolságra levő pontok halmaza micsoda?
|
|
| [2254] ilozagrav | 2007-08-26 21:30:33 |
 Sziasztok!
Komplex elemű mátrix főátlón kívüli elemeit rögzítjük. Bizonyítsuk be, hogy megválaszthatók a főátlóbeli elemek úgy, hogy a mátrix sajátértékei előre adottak,és hogy a mátrix sajátértékei az adott értékek legyenek.
|
|
| [2253] Q | 2007-08-26 09:25:09 |
 Köszi mindenkinek, rajta vagyok.
|
|
| [2252] Lóczi Lajos | 2007-08-26 00:57:11 |
 De a http://mathworld.wolfram.com/NewtonsIteration.html és http://mathworld.wolfram.com/LogisticMap.html oldalak igazi gyöngyszemek, amelyekből nemhogy órai előadást, de egész éves kurzust lehet tartani...
|
| Előzmény: [2251] Lóczi Lajos, 2007-08-26 00:53:37 |
|
| [2251] Lóczi Lajos | 2007-08-26 00:53:37 |
 Ebben a topikban több érdekes, rekurzióval kapcsolatos feladatot (és megoldást) találsz. (Javaslom, állítsd 200-ra a megjelenített hozzászólások számát és akkor elég hamar megtalálod az összeset.)
|
| Előzmény: [2247] Q, 2007-08-25 21:33:53 |
|
|
|
| [2248] ilozagrav | 2007-08-25 21:48:28 |
 Szia!
Pl. Pell egyenlet és másodrendű rekurzív sorozatok kapcsolata, elmehetsz a vektorterek irányába is,számtalan dolog lehet.Fibonacci sorozat stb.Nagy az irodalma üdv Zoli
|
| Előzmény: [2247] Q, 2007-08-25 21:33:53 |
|
| [2247] Q | 2007-08-25 21:33:53 |
 Sziasztok! Tudtok valami érdekes feladatot rekurzív sorozatokkal kapcsolatban? Órai előadáshoz kéne.
|
|
|
| [2245] ilozagrav | 2007-08-24 14:14:31 |
 Szia!
Én kreatív ötleteket várok.Egyébként egy normális halmazelmélet könyvben le van írva a válasz: Egy A halmaz számossága a legkisebb A-val ekvivalens rendszám. A kérdés az lenne inkább hogy találunk-e ilyen operációkat ami az előzőből nem triviálisan keletkezik.
|
| Előzmény: [2244] jonas, 2007-08-24 13:56:56 |
|








 X :oD
X :oD 



