|
|
| [2456] Sirpi | 2007-11-26 15:38:24 |
 Igazad van, ez kimaradt. Én úgy vettem, hogy lehet tükrözni. Bár az is érdekes lehet, hogy milyen különbség adódhat egy adott alakzat esetén, ha megengedjük, illetve ha nem engedjük meg a tükrözést.
És igen, én is 10-est találtam még az 1,2,4-en kívül. Vajon van más?
|
| Előzmény: [2454] Hajba Károly, 2007-11-26 14:26:42 |
|
|
|
| [2453] Sirpi | 2007-11-26 12:53:02 |
 Felmerült bennem egy probléma, egyelőre csak ízlelgetem. Az egyszerűség kedvéért nevezzünk rácsidomnak rácsnégyzetekből álló, élek mentén illeszkedő, összefüggő alakzatokat (gondoljatok a tetrisre, de nem feltétlen kell 4 kis négyzetből állnia az alakzatnak). Ezek között vannak olyanok, amiket többször felhasználva ki lehet rakni egy téglalapot, másokból meg nem. Az előbbiekhez rendeljük hozzá az ehhez szükséges minimális darabszámot. Tehát ha az alakzat eleve téglalap, akkor 1-et, a tetrisben pedig pl. az L-alakhoz 2-t, a T-alakhoz 4-et rendelünk.
A kérdés az, hogy mekkora lehet maximálisan ez a szám? Vagy egyáltalán, milyen más értékek adódhatnak így?
Mindenesetre találtam 4-nél nagyobbat már, innen jött az ötlet.
|
|
| [2452] Lóczi Lajos | 2007-11-25 22:46:37 |
 Nem olyan nehéz ez.
Tudjuk, hogy x, y és z pozitívak. Az x g(x,y,z) egy pozitív főegyütthatós másodfokú polinom. A gyökképlettel fejezzük ki a gyökeit, és mondjuk végezzük el az Y:=y2, Z:=z2, továbbá az A:=Y+Z, B:=YZ helyettesítéseket. Nyilván A2-4B g(x,y,z) egy pozitív főegyütthatós másodfokú polinom. A gyökképlettel fejezzük ki a gyökeit, és mondjuk végezzük el az Y:=y2, Z:=z2, továbbá az A:=Y+Z, B:=YZ helyettesítéseket. Nyilván A2-4B 0, A>0, B>0. 0, A>0, B>0.
Azt kapjuk, hogy
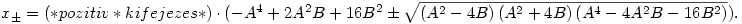
Ki akarjuk zárni, hogy g<0 pozitív x-ekre.
Ha a diszkrimináns negatív, készen vagyunk.
Ha a diszkrimináns A2-4B miatt nulla, szintén készen vagyunk, mert ez annak felel meg, ha y=z, de 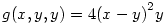 . .
Elég tehát az A4-4A2B-16B2 0 esetben megvizsgálni, hogy a nagyobbik gyök, x+ lehet-e pozitív. 0 esetben megvizsgálni, hogy a nagyobbik gyök, x+ lehet-e pozitív.
Elemi módon látszik, hogy A4-4A2B-16B2 0 és -A4+2A2B+16B2 0 és -A4+2A2B+16B2 0 és A2-4B 0 és A2-4B 0 egyszerre nem teljesülhetnek a pozitív számpárok körében. 0 egyszerre nem teljesülhetnek a pozitív számpárok körében.
Az kell tehát csak megnézni, mi van, ha -A4+2A2B+16B2 0 (a diszkrimináns előjelére nem is kell most figyelni). Ekkor átrendezve és négyzetre emelve az x+>0 egyenlőtlenséget (mindkét oldal nemnegatív!), azt kapjuk, hogy A4B2<0, ami nem lehet. A bizonyítás készen van. 0 (a diszkrimináns előjelére nem is kell most figyelni). Ekkor átrendezve és négyzetre emelve az x+>0 egyenlőtlenséget (mindkét oldal nemnegatív!), azt kapjuk, hogy A4B2<0, ami nem lehet. A bizonyítás készen van.
|
| Előzmény: [2450] Lóczi Lajos, 2007-11-25 20:32:12 |
|
| [2451] Róbert Gida | 2007-11-25 20:51:55 |
 Igen, ezt kell belátni, nem szabadott volna négyzetre emelnem, mert a jobb oldal negatív is lehet, köszönhetően annak, hogy: igaz, hogy R 2*r teljesül, de R bármekkora lehet rögzített r mellett. 2*r teljesül, de R bármekkora lehet rögzített r mellett.
Egyébként szabályos háromszögre egyenlőséggel, ez megfelel x=y=z-nek és g(x,x,x)=0
|
| Előzmény: [2450] Lóczi Lajos, 2007-11-25 20:32:12 |
|
|
|
| [2448] Róbert Gida | 2007-11-25 16:29:22 |
 Hm, a polinom lexikografikusan legnagyobb tagjának negatív az együtthatója, ergó számtani-mértani egyenlőtlenségekkel ezt nem lehet belátni.
A polinom egyébként homogén hatodfokú, így feltehető például, hogy x=1 teljesül. (Kicsivel rövidebb lesz akkor a képlet.)
|
| Előzmény: [2446] Róbert Gida, 2007-11-25 16:14:49 |
|
|
| [2446] Róbert Gida | 2007-11-25 16:14:49 |
 A következőkkel próbálkoztam:
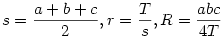
Majd egy háromszögekre való egyenlőtlenség bizonyításának ismert technikája: legyen
x=s-a,y=s-b,z=s-c
Ekkor x,y,z>0 teljesül, megfordítva minden pozitív x,y,z-re tartozik pontosan egy háromszög. (oldalaira a háromszög-egyenlőtlenség teljesül). Ezt beírva és négyzetre emelve és rendezve az oldalt kapjuk: f(x,y,z)=4yz(x+z)2(x+y)2-(16xyz-(x+y)(y+z)(z+x))2 kell teljesülnie minden pozitív x,y,z számokra. Ez a polinom viszont a maple szerint irreducibilis a racionális többváltozós test felett. Egy nehéz módszer ilyenkor, hogy számtani-mértani egyenlőtlenségek tucattyaival igazolni, hogy f(x,y,z) pozitív, de ennek a megtalálása egyáltalán nem triviális, illetve van amikor nem is lehetséges, annak ellenére, hogy az egyenlőtlenség igaz.
|
| Előzmény: [2443] Gyöngyő, 2007-11-25 13:26:07 |
|
|
|
| [2443] Gyöngyő | 2007-11-25 13:26:07 |
 Sziasztok!
Lenne egy kis feladatom,amivel nem nagyon tudok megbirkozni:
adva van egy általános háromszög ahol r,R a szokásos dolgok.p=kerület fele,a,b,c az oldalak hossza. Bizonyítsuk be,hogy:
a/2*((4r-R)/R)=<gyok((p-b)(p-c).
Köszönettel:
Zsolt
|
|
| [2442] Python | 2007-11-25 12:37:22 |
 a.) Nem lehet. Ha A-t csak 2 ember, B és C győzte le, akkor A-t és B-t mindkettőjüket csak C győzhette le, így B-t C legyőzi, de A-t és C-t csak B győzhette le, így C-t B legyőzi, de ez ellentmondás, így mindenkit legalább 3-an legyőznek, de ehhez 6.3=18 meccs kell, de csak 15 meccs van.
|
| Előzmény: [2439] rizsesz, 2007-11-23 10:23:55 |
|
| [2441] kisevet7 | 2007-11-23 15:26:42 |
 Sziasztok! Köszönöm a megoldásokat! Sajnálom, hogy nem voltam gépnél az előző 2 napban, így nem tudtam válaszolni a kérdésekre, de természetesen a szimmetria miatt (mármint hogy mindenki kaszabolja a másikat, csak más hatákonysággal) igaz a másik összefüggés is. Sirpi! Esetleg találkoztál azzal az ese4ttel is, ahol az egyik csapat hagyományosan kaszabol, a másik gerillaharcot folytat (amikoris a gerillákat meg is kell keresni), és ahol az összefüggés x'(t)=bx(t)y(t)? (x harcol hagyományosan, y a gerilla)
|
|
| [2440] Sirpi | 2007-11-23 14:25:47 |
 Az integrálással kapott egyenleted átrendezve:
ay2(t)-bx2(t)=ay2(0)-bx2(0)
Vagyis az f(t)=ay2(t)-bx2(t) függvény igazából nem függ t-től, és értéke ugyanannyi, mint kezdetben.
Ebből pl. kijön az a szerintem meglepő dolog, hogy egy 5000-es és egy 4000-es sereg ütközetekor (azonos tudású katonákat feltételezve) a győztes csapatnak 3000(!) katonája marad életben. 13000 vs. 12000 esetén pedig 5000.
Én biztos, hogy magamtól sokkal kevesebbre tippeltem volna (korábban magam is felvetettem és megoldottam ezt a feladatot, és már akkor megdöbbentett az eredmény).
|
| Előzmény: [2434] wernerm, 2007-11-21 22:19:43 |
|
| [2439] rizsesz | 2007-11-23 10:23:55 |
 Sziasztok!
Lehetséges-e az egy a., 6, b., 7 fős társaságban, ahol mindenki játszik mindenkivel (mondjuk sakkoznak) hogy bármely 2 emberhez található egy olyan 3., aki megverte mindkettejüket?
|
|
| [2438] nadorp | 2007-11-23 08:10:45 |
 Bocs, helyesen:
Gondolom a feladat úgy van modellezve, hogy az y sereg egy katonája mondjuk percenként "a" darab ellenséget tud legyőzni, az x sereg egy katonája pedig percenként "b" darabot és feltesszük, hogy ezt egyenletesen teszik.
|
| Előzmény: [2437] nadorp, 2007-11-23 08:06:15 |
|
| [2437] nadorp | 2007-11-23 08:06:15 |
 Gondolom a feladat úgy van modellezve, hogy az y sereg mondjuk percenként "a" darab ellenséget tud legyőzni, az x sereg pedig percenként "b" darabot és feltesszük, hogy ezt egyenletesen teszik.
|
| Előzmény: [2436] wernerm, 2007-11-22 22:22:09 |
|
| [2436] wernerm | 2007-11-22 22:22:09 |
 Ha nem lenne az az egyenlet, akkor tetszőleges y(t)-t beírhatnék, és abból x(t)-t integrálással kapnám.
A feladat kitűzője valóban nem írt y'(t) és x(t) közötti összefüggésről, de mivel két hadseregről van szó, a dolog elég szimmetrikusnak tűnik, ezért tettem fel egy ilyen alakú egyenletet.
üdv: Miklós
|
| Előzmény: [2435] Lóczi Lajos, 2007-11-22 11:44:44 |
|
|
| [2434] wernerm | 2007-11-21 22:19:43 |
 Nézzük meg, hogy az idő elteltével egymáshoz viszonyítva hogyan változnak a hadseregek. (A pontos időbeli lefutás nem lényeges, csak az a lényeg, ki nyer.)
x'(t)=-ay(t)
-bx(t)=y'(t)
Szorozzuk össze a két egyenletet!
ay(t)y'(t)=bx(t)x'(t)
Integráljuk mindkét oldalt 0-tól t-ig határozottan.
ay2(t)/2-ay2(0)/2=bx2(t)/2-bx2(0)/2
.
Átrendezve ez az x-y síkon egy hiperbola egyenlete. A végső állapotot az jelenti, ha elmetszük valamelyik tengelyt. Amelyik tengelyt elmetszettük, az a sereg győzött. (Nekik maradt katonájuk).
Az x csapat győz, ha bx2é(0)-ay2(0)>0, fordított relációnál az y csapat.
Érdekes a helyzet az egyenlőségnél. Ekkor a két sereg kölcsönösen lekaszabolja egymást.
A katonák kis létszáma esetén lényegessé válik az, hogy a katonák száma egész.
|
| Előzmény: [2433] kisevet7, 2007-11-21 20:48:07 |
|





 g(x,y,z) egy pozitív főegyütthatós másodfokú polinom. A gyökképlettel fejezzük ki a gyökeit, és mondjuk végezzük el az Y:=y2, Z:=z2, továbbá az A:=Y+Z, B:=YZ helyettesítéseket. Nyilván A2-4B
g(x,y,z) egy pozitív főegyütthatós másodfokú polinom. A gyökképlettel fejezzük ki a gyökeit, és mondjuk végezzük el az Y:=y2, Z:=z2, továbbá az A:=Y+Z, B:=YZ helyettesítéseket. Nyilván A2-4B 0, A>0, B>0.
0, A>0, B>0.  0 (a diszkrimináns előjelére nem is kell most figyelni). Ekkor átrendezve és négyzetre emelve az x+>0 egyenlőtlenséget (mindkét oldal nemnegatív!), azt kapjuk, hogy A4B2<0, ami nem lehet. A bizonyítás készen van.
0 (a diszkrimináns előjelére nem is kell most figyelni). Ekkor átrendezve és négyzetre emelve az x+>0 egyenlőtlenséget (mindkét oldal nemnegatív!), azt kapjuk, hogy A4B2<0, ami nem lehet. A bizonyítás készen van. 



