| [2495] Cckek | 2007-12-14 22:43:57 |
 Krimirajongóként, anélkül hogy kötekedni akarnék, megkérdem, hogy nem Moriarty professzorról van szó? Amúgy nagyon érdekes feladat, én léggyel meg pókhálóval tudom, a pók útolérheti a legyet ha a pókháló tartalmaz háromszöget.
|
| Előzmény: [2492] Enkidu, 2007-12-12 12:45:22 |
|
|
| [2493] Lóczi Lajos | 2007-12-14 00:04:44 |
 Van-e olyan kétváltozós f függvény, hogy 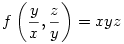 , azaz kifejezhető-e xyz, mint y/x és z/y függvénye? , azaz kifejezhető-e xyz, mint y/x és z/y függvénye?
|
|
| [2492] Enkidu | 2007-12-12 12:45:22 |
 A megoldásod teljesen jó! A 15-ös korlátot csak azért adtam, mert matekórán játszottunk párat gyerekekkel, én sem tudom pontosan, mennyi a legkevesebb lépés (ha Mortimer jól játszik); a lényeg az, hogy ha Holmes áthalad Rejkjavikon, akkor (állandóan közelítve Mortimerhez) 7-8 lépés alatt elkapja.
Szóval ez tényleg csak egy egyszerű játék volt, és nagyon hasonló a megoldása (Rejkjavik nélkül a gráf 2-színezhető lenne - Rejkjavikkal a kromatikus szám 3) is mint a korábbi példának, azért gondoltam, hogy megmutatom.
Sziasztok!
|
| Előzmény: [2491] HoA, 2007-12-11 14:19:06 |
|
| [2491] HoA | 2007-12-11 14:19:06 |
 A Holmes vs. Mortimer feladatban [2479] ezek után világos, hogy ha Rejkjavikot egyik sem érinti, Holmes Pétervárról, Mortimer Párizsból indul és Holmes lép elsőnek, akkor Holmes soha sem léphet abba a városba, ahol éppen Mortimer van. ( Fordítva igen, de Mortimernek ez nyilván nem célja. ) A megoldásnak tehát szükséges feltétele, hogy egyikük érintse egyszer Rejkjavikot. ( Precízen: A két ellenfél rejkjaviki utazásainak száma különböző paritású legyen ) . A továbbiakat nem látom. Hol jön be a 15-ös lépéskorlát? Biztos, hogy nincsenek szigorúbb feltételek? Pl. Mortimer nem mehet kétszer ugyanabba a városba? Az elfogás vége is világos: Ha Mortimer "A" városban van mikor Holmesnak sikerül "B" városba lépnie úgy, hogy "A" minden szomszédja egyben "B" -nek is szomszédja, Holmes nyert. Ilyen például A = Madrid B = Párizs. De hogyan kényszerítheti Mortimert ilyen lépésre? Szabad a gazda.
|
| Előzmény: [2479] Enkidu, 2007-12-05 13:31:00 |
|
| [2490] HoA | 2007-12-07 15:17:43 |
 Én [2476] -ban arra céloztam, hogy ha behúzzuk az AM élt, G gráfunkból egy szép szimmetrikus G' gráfot kapunk, ahol minden csúcs fokszáma 3 vagy 4, és a 8 éves is könnyen észreveheti, hogy 3-adfokú csúcsnak csak 4-edfokú szomszédja van és viszont. Innen adódik a 8 piros - 6 zöld alapú megoldás. És persze ha G' -nek nincs Hamilton útja, akkor G-nek sem lehet.
|
| Előzmény: [2489] Csimby, 2007-12-07 02:21:30 |
|
| [2489] Csimby | 2007-12-07 02:21:30 |
 A színezésből látszik, hogy két piros ill. két zöld csúcs között nem megy él, hanem él csak piros és zöld csúcsok között megy. Így bármely úton/körön felváltva kell hogy következzenek a piros ill. zöld csúcsok. De mivel piros csúcsból 8, zöld csúcsból pedig csak 6 van így váltakozó piros-zöld sorozatból legfeljebb csak 13 hosszút tudunk csinálni. Azt pedig, hogy a gráf kétszínnel színezhető - vagyis páros - lehetett megsejteni abból, hogy benne minden kör páros volt, ez a két állítás ekvivalens. Persze csak abból, hogy a gráf páros még nem következik hogy nincs benne Hamilton út, ehhez még kellett, hogy a két osztály (piros és zöld csúcsok) elemszámának a különbsége 2.
|
| Előzmény: [2488] szbela, 2007-12-07 01:38:08 |
|
| [2488] szbela | 2007-12-07 01:38:08 |
 Sziasztok!
Ez egy olyan megoldás lenne, ahol arra a tételre hivatkozol, hogy ha van a gráfban Hamilton-kör, akkor k csúcs és az ezekből induló élek elhagyásával a gráf legfeljebb k komponensre esik szét? A zöld (6db) pontok elhagyásával a gráf 8 db komponensre esik szét, azaz nincs Hamilton-köre.
|
| Előzmény: [2485] jonas, 2007-12-06 19:41:31 |
|
|
|
|
| [2484] Csimby | 2007-12-06 19:30:59 |
 Nem kell program. Van "szép" megoldás is, tehát nem ilyen esetszétválasztgatós. Mondjuk nekem hogy rájöjjek kellett valami amit véges matekon tanultunk az egyetemen.
|
|
| [2483] jonas | 2007-12-06 19:22:38 |
 Lefuttattam rá egy kimerítő keresést. Nem volt nehéz, mivel csak 14 csúcs van, és minden csúcsból csak legfeljebb három irányba lehet továbbmenni.
Ha helyes a programom, akkor nincs benne Hamilton-út.
Ha megengedjük, hogy egy csúcsot kihagyjunk, akkor pl. a következő útvonal jó: ACHMNLKIJFGBD.
|
| Előzmény: [2467] Csimby, 2007-12-04 01:26:25 |
|
|
|
| [2480] Enkidu | 2007-12-05 13:41:13 |
 A bizonyítás:
Nyolc ember között van olyan, aki legalább négy másikat elvert. Ő lesz a győztesünk. Vizsgáljuk azt a négy embert, akiket megvert. Ezen négyesben van olyan ember, aki a másik három ember közül kettőt elvert, ő lesz a "második". Az a két ember, akiket ez az utóbbi elvert eldöntik egymás között, ki a harmadik és a negyedik. Ezzel kész.
Ha hét emberre vizsgálnánk, akkor már nem feltétlenül teljesül; ha pl (megszámozva a versenyzőket) mindenki elveri a nála 1,2 és 4-gyel nagyobb sorszámút (modulo 7 gondolkozva - ennyi pontatlanság talán belefér:)), akkor az egy ellenpélda.
|
| Előzmény: [2466] Csimby, 2007-12-04 01:19:45 |
|
| [2479] Enkidu | 2007-12-05 13:31:00 |
 Egy ezzel a példával kapcsolatos aranyos (bár elég egyszerű) példa a következő:
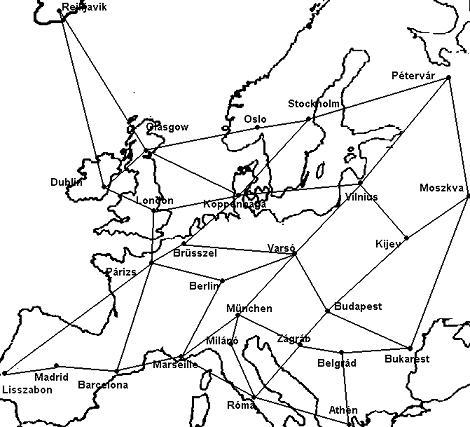
Sherlock Holmes ősi ellenfele Mortimer ellopta a Mona Lisát a párizsi Louvre-ból. Holmes éppen Péterváron volt és rögtön repülőre ült, hogy elkapja a gazfickót. (Európa repülőtereit a lenti ábra mutatja; egy lépésben csak egy szomszédos repülőtérre repülhetünk, azaz pl Pétervárról közvetlenül csak Moszkva, Vilnius és Stockholm érhető el.) Miután Holmes lépett egyet Mortimernek is lépnie kell (ha túl sokáig maradna egy helyen elkapnák a rendőrök). Vagyis a két játékos felváltva lép. Ha Holmesnak sikerül ugyanabba a városba repülnie, ahol éppen akkor Mortimer tartózkodik, akkor elkapja és vége a játéknak. Ha Mortimer 15 lépés után is szabad, végleg megmenekült. El lehet-e fogni Mortimert? Ha igen, hogyan?
|
 |
| Előzmény: [2468] rizsesz, 2007-12-04 08:45:58 |
|
|
|
| [2476] HoA | 2007-12-05 11:11:43 |
 Nem is tudom, most örüljek-e, hogy sikerült rájönni egy megoldásra, amihez valóban elég egy 8 éves tudása. Az ebben a megoldásban felhasznált tulajdonság felismeréséhez nem a 10 négyszög léte, hanem az segít, ami hiányzik az ábráról :-)
|
| Előzmény: [2474] rizsesz, 2007-12-04 14:05:10 |
|
|
|
| [2473] Hajba Károly | 2007-12-04 14:01:11 |
 A vonalak 10 db négyszöget határoznak meg. Ha ezeket átalakítjuk egy újabb gráffá úgy, hogy a négyzetek a gráfcsúcsok és a csatlakozó él az új gráf élei, akkor ebben a gráfban is meg kellene tudni csinálni az összekötést. Ha nem sikerül, akkor az eredetiben sem lehet.
Persze tudom ez nem bizonyítás. Inkább csak morfondíroztam egyet. :o)
|
| Előzmény: [2471] Csimby, 2007-12-04 12:47:51 |
|
| [2472] rizsesz | 2007-12-04 13:58:02 |
 Akkor gondolj arra, hogy a hivatalos megoldás tulajdonosa 2. osztályos volt. És nem középiskolás, hanem általános iskolás, azaz 8 éves. Szóval érdemes elrugaszkodni egy kicsit attól, amit az ember tud, és olyan fejjel gondolkodni, mintha csak nagyon alapvető eszközeink lennének. :)
|
| Előzmény: [2470] Hajba Károly, 2007-12-04 12:38:43 |
|
| [2471] Csimby | 2007-12-04 12:47:51 |
 Szerintem is egy szép feladat :-) Ha alég sokáig nézi az ember a gráfot, akkor észre lehet venni valamit ami nagyon sokat segít.
|
|