|
| [2883] Tibixe | 2009-03-11 18:09:52 |
 Ha jól látom, a lenti megoldás általánosítható 2c sok színre, mert egy színt meghatároz az, hogy melyik együtthatót követeljük nemnegatívnak és melyiket negatívnak. És kontinuum sok együttható van.
Színek egyesítésével pedig megkaphatunk bármilyen ennél kisebb számosságot.
Jól látom?
|
|
|
| [2881] jenei.attila | 2009-03-11 12:03:31 |
 Válaszolnék az alábbi valóban érdekes feladatra:
"Ki lehet-e színezni a pozitív valós számokat pirosra és kékre(mindkét színt kell használni), hogy pirosak összege piros, kékek összege kék legyen?"
Sokat agyaltam rajta, és úgy tűnik van ilyen színezés. A "valaki mondja meg" topikban feltettem néhány valós számokra vonatkozó algebrai kérdést, azokat is ez a feladat hozta elő. Tekintsük a valós számok testét a racionális számok teste feletti vektortérnek. Ennek a vektortérnek a bázisát Hamel bázisnak nevezik. Vagyis igaz az, hogy létezik a valós számok halmazának olyan H részhalmaza (ez a Hamel bázis), amellyel minden valós szám egyértelműen áll elő
r1h1+...+rnhn
alakban, ahol az r együtthatók racionális számok, a h számok pedig H elemei és n véges de függ az előállítandó számtól. Feltehetjük, hogy H tartalmazza az 1-et, és r1 az 1 együtthatója. Minden így előállított valós számot színezzünk pirosra, ha a h1 együttható (a szám "racionális része") nem negatív, kékre, ha r1 negatív. Így nyilván a valós számoknak egy jó színezését adjuk meg, és lesz kék pozitív szám is (pl. 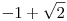 , ha a , ha a 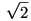 is eleme H-nak). is eleme H-nak).
|
| Előzmény: [2804] kutasp, 2009-01-07 22:02:55 |
|
| [2880] sakkmath | 2009-03-07 17:03:18 |
 Igazoljuk, hogy ha 1 < a < b < c, akkor
loga(logab) + logb(logbc) + logc(logca) > 0.
|
|
|
|
| [2877] Tibixe | 2009-02-16 19:38:07 |
 A
z1=i z2=-i
esetben nálam
|z1|=1
|z2|=1
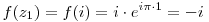
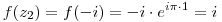
Tehát
f(i)-f(-i)=-2i
és
i-(-i)=2i
ezek aránya -1.
Abszolút értékeik aránya pedig 1.
És ez a két arány csak előjelben különbözik.
Elrontottam volna valamit?
|
| Előzmény: [2876] Cckek, 2009-02-15 21:12:42 |
|
|
|
|
|
|
| [2871] psbalint | 2009-01-26 17:02:35 |
 megnézed azt a kis nyilacskás részt, és mindegyik elemhez hozzárendeled a tőle jobbra, három nyilacskára álló elemet :)
|
|
|
| [2869] S.Ákos | 2009-01-25 21:17:30 |
 63=12.5+3, szóval: P63=P60+3=(P5)12.P3=P3 A párosítás pedig abból adódott, hogy külön-külön megnézzük az egyes elemeknél, hogy P háromszori elvégzése mit rendel hozzá az adott elemhez.
|
| Előzmény: [2868] mmarta, 2009-01-25 19:02:42 |
|
|
|
| [2866] mmarta | 2009-01-25 11:53:47 |
 Sziasztok! Segítséget szeretnék én is kérni a köv. feladathoz. 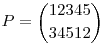 Adja meg a P63 permutációt. Egyszerű, szájbarágós magyarázat, megoldás kellene, hogy meg is értsem :) Adja meg a P63 permutációt. Egyszerű, szájbarágós magyarázat, megoldás kellene, hogy meg is értsem :)
Köszönöm
|
|
| [2865] Kemény Legény | 2009-01-24 02:18:24 |
 Hát, semmi sem elég jó Neked :)
Rendben, akkor az új "tétel": 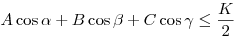
Az ezzel egyenértékű 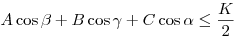 és és 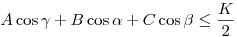
egyenlőtlenségek összege 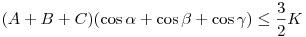
Ismert, hogy 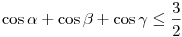
Tehát valamelyik állítás igaz, azaz a "szokásos érvvel" az összes is, a tételt "beláttuk".
Ezt mutatja nyilván az 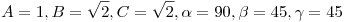 példa is, amikor példa is, amikor 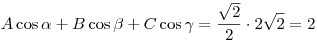
Míg a jobb oldal 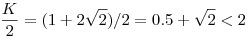
Amit csináltam az eredeti "bizonyítás" kapcsán, hogy lehagytam a 2-es kitevőket, és a koszinuszra cseréltem a kotangenst, és a jobb oldalra a kerület konstansszorosa került. Ha még mindig vannak ellenvetéseid (pl. szép-szép, de egy kontangenses ellenpélda még szebb lenne, sőt miért nem cáfolom meg rögtön az eredetileg kitűzött A-feladatot is), akkor szólj bátran.
|
| Előzmény: [2864] rizsesz, 2009-01-23 23:47:26 |
|
|
| [2863] Kemény Legény | 2009-01-23 17:45:05 |
 Ha csak az kell, tudok én egyenértékű állításokból is ellenpéldát mutatni. Legyenek 2 háromszög oldalai A,B,C és a,b,c, kerületeik K,k. Állítás: 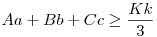 Egyenértékű ezzel: Egyenértékű ezzel: 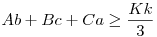 Szintén egyenértékű: Szintén egyenértékű: 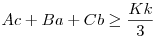
Összeadva a 3 egyenlőtlenséget: a bal oldal (A+B+C)(a+b+c)=Kk azaz valamelyikük igaz, ekkor az "elv" miatt mindhárom igaz.
Ellenpélda: (A=2,B=2,C=3,a=1,b=1,c=0.1,K=7,k=2.1,Aa+Bb+Cc=2+2+0.3=4.3<4.9=Kk/3)
|
| Előzmény: [2862] rizsesz, 2009-01-23 10:55:57 |
|
| [2862] rizsesz | 2009-01-23 10:55:57 |
 Én értem ezt a logikai utat. Pontosan ezért kérdeztem rá. Jelen esetben azonban ha akármelyik igaz, az egyenértékű az állítással.
Ezzel szemben az általad adott példában a 3 állítás nem egyenértékű.
Azt is értem, hogy az eredeti állításból nem juthatunk el a + 2 általam felírt egyenlőtlenséghez.
Szóval már majdnem meggyőztél, de még kötözködöm :)
|
| Előzmény: [2861] Kemény Legény, 2009-01-23 10:11:10 |
|
| [2861] Kemény Legény | 2009-01-23 10:11:10 |
 Az eredeti "bizonyítás" során a 3 állítás bármelyikének igazolása önmagában elegendő lenne a teljes megoldáshoz, de onnantól kezdve, hogy mindhármat felírtuk egyszerre, akkor már csak azt tudjuk belátni, hogy minden háromszögben valamelyik igaz. Abból pedig, hogy egy állítás egy tetszőleges háromszögben igaz az oldalak/szögek valamilyen sorrendjére, nem következik, hogy minden háromszögben az oldalak/szögek tetszőleges sorrendjére igaz lenne.
Az állítások felírásában valóban nincs kitüntetett szerepe semminek, de amikor találunk egyet a 3 közül, ami igaz, abban már az oldalak/szögek egy kitüntetett sorrendben szerepelnek, és épp ez veszi el az általánosítás lehetőségét.
|
| Előzmény: [2856] rizsesz, 2009-01-23 02:06:57 |
|
| [2860] rizsesz | 2009-01-23 09:14:59 |
 Ugyanis ha már az egyik igaz, akkor mivel a szorzók nincsenek meghatározva, így bármilyen formában odapakolhatod őket az oldalak mellé együtthatónak.
Szóval szerintem az én logikám nem alkalmazható az a+b+4c-s példára.
|
| Előzmény: [2858] Valezius, 2009-01-23 06:41:45 |
|




 esetén [C : K] is véges volna, ami az Artin-Schreier tétel szerint csak a K=R esetben lehet. Másrészt, ha A
esetén [C : K] is véges volna, ami az Artin-Schreier tétel szerint csak a K=R esetben lehet. Másrészt, ha A R egy maximális (nyilván
R egy maximális (nyilván 

 intervallumon
intervallumon
 z2 melyeknek az abszolut értéke is különbözik? Amugy itt van még egy kérdés: Bizonyitsuk be, hogy létezik
z2 melyeknek az abszolut értéke is különbözik? Amugy itt van még egy kérdés: Bizonyitsuk be, hogy létezik  >0 úgy hogy, ha
>0 úgy hogy, ha  nem egyidejűleg áll fenn. Tehát vagy baloldal =+ jobboldal vagy baloldal =- jobboldal.
nem egyidejűleg áll fenn. Tehát vagy baloldal =+ jobboldal vagy baloldal =- jobboldal.  1 komplex számok melyekre:
1 komplex számok melyekre: 

 3
3 , ctg
, ctg , ctg
, ctg variálása nem befolyásolja a másik oldalt (T, amely csak A, B és C által meghatározott).
variálása nem befolyásolja a másik oldalt (T, amely csak A, B és C által meghatározott).