| [2922] jenei.attila | 2009-04-20 09:15:07 |
 Először én is a skatulya elvvel hasonló módon próbáltam bizonyítani mint te, mert intuitíve elég nyilvánvalónak tűnik, hogy az {nx} (x rögzített irracionális, n végigfut az egészeken) sűrű [0,1] intervallumban és nem maradnak rések. Egy kicsit tovább gondolva azért rendbe lehet tenni ezt a bizonyítást: osszuk a [0,1] intervallumot N egyenlő részre, ahol 1/N< . Akkor a skatulya elv szerint ahogy írtad, léteznek i és j természetes számok, hogy {ix} és {jx} ugyanabba az 1/N hosszúságú részintervallumba esnek és különbözőek (mivel x irracionális). Ezért {ix}-{jx}< . Akkor a skatulya elv szerint ahogy írtad, léteznek i és j természetes számok, hogy {ix} és {jx} ugyanabba az 1/N hosszúságú részintervallumba esnek és különbözőek (mivel x irracionális). Ezért {ix}-{jx}< , amiből {(i-j)x}< , amiből {(i-j)x}< következik (feltehető hogy i>j). Definíció szerint legyen h:={(i-j)x}. Mivel h< következik (feltehető hogy i>j). Definíció szerint legyen h:={(i-j)x}. Mivel h< , ezért [0,1] minden 1/N hosszúságú részintervallumában megtalálható lesz h-nak valamelyik többszöröse. Tehát tetszőlegesen kiválasztva egy részintervallumot, valamely k természetes számmal kh eleme lesz ennek a részintervallumnak. Azonban kh=k{(i-j)x}={k(i-j)x}, azaz ha m-et k(i-j) -nek definiáljuk, x-nek olyan mx többszörösét kapjuk, amelynek törtésze az előre kiválasztott 1/N hosszú részintervallumban van. Ez pedig már tényleg azt jelenti, hogy {nx} sűrű [0,1]-ben. Visszatérve az irracionális számok másodrendű racionális közelíthetőségére: úgy tűnik, hogy ez és a most skatulyaelvvel bizonyított állítás ekvivalensek. Tehát próbáljuk meg skatulyaelvvel bizonyítani, hogy tetszőleges x irracionális számra végtelen sok a,b természetes szám létezik, hogy , ezért [0,1] minden 1/N hosszúságú részintervallumában megtalálható lesz h-nak valamelyik többszöröse. Tehát tetszőlegesen kiválasztva egy részintervallumot, valamely k természetes számmal kh eleme lesz ennek a részintervallumnak. Azonban kh=k{(i-j)x}={k(i-j)x}, azaz ha m-et k(i-j) -nek definiáljuk, x-nek olyan mx többszörösét kapjuk, amelynek törtésze az előre kiválasztott 1/N hosszú részintervallumban van. Ez pedig már tényleg azt jelenti, hogy {nx} sűrű [0,1]-ben. Visszatérve az irracionális számok másodrendű racionális közelíthetőségére: úgy tűnik, hogy ez és a most skatulyaelvvel bizonyított állítás ekvivalensek. Tehát próbáljuk meg skatulyaelvvel bizonyítani, hogy tetszőleges x irracionális számra végtelen sok a,b természetes szám létezik, hogy 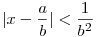
|
| Előzmény: [2920] jonas, 2009-04-19 16:08:39 |
|
| [2921] jenei.attila | 2009-04-19 17:14:21 |
 Sajnos még mindig nem értem. Amikor ezt írod "{floor(np)} sűrű a [0..1] intervallumon"; itt a floor mit jelent? Az alsó egészrész? Ez ugye nem kell. Az állítás szerintem: tetszőleges adott p irracionális számra az {np} alakú számokból álló halmaz (ahol n végig fut az egész számokon) sűrű [0,1]-ben. "Vegyük most a p első 1/ többszörösét, vagyis a p,2p,3p,...,ceil(1/ többszörösét, vagyis a p,2p,3p,...,ceil(1/ )p számokat. Ezek mindegyike 0 és 1 közé esik" ezt szintén nem értem. Ha pl )p számokat. Ezek mindegyike 0 és 1 közé esik" ezt szintén nem értem. Ha pl  , akkor p többszörösei nem esnek 0 és 1 közé. Itt valószínűleg a többszörösök törtrészére gondoltál. "Az np törtrész többszöröseiről nem azt mondom, hogy sűrűek, hanem csak azt, hogy legfeljebb , akkor p többszörösei nem esnek 0 és 1 közé. Itt valószínűleg a többszörösök törtrészére gondoltál. "Az np törtrész többszöröseiről nem azt mondom, hogy sűrűek, hanem csak azt, hogy legfeljebb  távolságra vannak egymástól". Itt szerintem az np többszörösök törtrészeire gondoltál. Azt nem értem, hogy ezekről mi alapján állítod, hogy "legfeljebb távolságra vannak egymástól". Itt szerintem az np többszörösök törtrészeire gondoltál. Azt nem értem, hogy ezekről mi alapján állítod, hogy "legfeljebb  távolságra vannak egymástól". Mert az OK, hogy van olyan távolságra vannak egymástól". Mert az OK, hogy van olyan  hosszú intervallum, amelybe p legalább két többszörösének törtrésze esik, de miből tudjuk, hogy nem marad ki valamely hosszú intervallum, amelybe p legalább két többszörösének törtrésze esik, de miből tudjuk, hogy nem marad ki valamely  hosszú intervallum? Nem akarlak megsérteni, de szerintem ez a bizonyításod így nem jó. Esetleg ha agy numerikus példán mutatnád be... hosszú intervallum? Nem akarlak megsérteni, de szerintem ez a bizonyításod így nem jó. Esetleg ha agy numerikus példán mutatnád be...
|
| Előzmény: [2920] jonas, 2009-04-19 16:08:39 |
|
| [2920] jonas | 2009-04-19 16:08:39 |
 A bizonyítást tényleg nem igazán jól írtam le.
Az np törtrész többszöröseiről nem azt mondom, hogy sűrűek, hanem csak azt, hogy legfeljebb  távolságra vannak egymástól, így bármilyen valós számhoz van legfeljebb távolságra vannak egymástól, így bármilyen valós számhoz van legfeljebb  /2 távolságra egy többszörös. Mivel azonban ez minden /2 távolságra egy többszörös. Mivel azonban ez minden  -ra igaz, ezért a p összes többszörösének törtrészei már sűrűek a [0..1]-ben. -ra igaz, ezért a p összes többszörösének törtrészei már sűrűek a [0..1]-ben.
Azt, hogy p irracionális, ott használtam föl, hogy a p többszöröseinek törtrészei nem esnek egybe, mert ellenkező esetben előfordulhatna, hogy a két egy intervallumba eső egészrész valójában egyenlő, vagyis floor(np)=0, amikor is a bizonyítás nem működik.
|
| Előzmény: [2918] jenei.attila, 2009-04-19 15:47:28 |
|
|
| [2918] jenei.attila | 2009-04-19 15:47:28 |
 Az igaz, hogy lesz olyan epszilon hosszú intervallum amelyikbe két többszörös kerül. De ez még nem biztosítja azt, hogy nem lesz olyan epszilon hosszú intervallum, amibe egy többszörös sem kerül. Márpedig a mindenhol sűrűséghez ez kéne. np többszörösei pedig természetesen nem sűrűek R-ben. Az np+k már igen. Továbbra is fenntartom, hogy a mindenhol való sűrűséghez kell, hogy p mint irracionális szám, elsőrendűnél jobban legyen közelíthető racionálisan. Egyébként a te bizonyításodban hol használjuk ki, hogy p irracionális? Mert ha p racionális, akkor is igaz lehet amit mondasz (lesz két olyan np és kp amelyek egy intervallumba esnek).
|
| Előzmény: [2917] jonas, 2009-04-19 15:14:31 |
|
| [2917] jonas | 2009-04-19 15:14:31 |
 Azt szerintem is ki kell használni, hogy ha p irracionális, akkor {floor(np)} sűrű a [0..1] intervallumon. Erre viszont én egy másik bizonyítást találok természetesnek, mégpedig a következőt.
Rögzítsük a 0< számot. Osszuk fel a [0..1] intervallumot 1/ számot. Osszuk fel a [0..1] intervallumot 1/ egyforma részre: [0.. egyforma részre: [0.. ],[ ],[ ..2 ..2 ],...,[floor(1/ ],...,[floor(1/ ) ) ..floor(1+1/ ..floor(1+1/ ) ) ], mindegyik ], mindegyik  hosszú. Vegyük most a p első 1/ hosszú. Vegyük most a p első 1/ többszörösét, vagyis a p,2p,3p,...,ceil(1/ többszörösét, vagyis a p,2p,3p,...,ceil(1/ )p számokat. Ezek mindegyike 0 és 1 közé esik, és annyi van belőlük, mint intervallum, így kell lennie egy intervallumnak, ahova kettő esik. Ennek a két többszörösnek a különbsége abszolutértékben legfeljebb )p számokat. Ezek mindegyike 0 és 1 közé esik, és annyi van belőlük, mint intervallum, így kell lennie egy intervallumnak, ahova kettő esik. Ennek a két többszörösnek a különbsége abszolutértékben legfeljebb  , legyen ez a különbség mondjuk 0<floor(np)< , legyen ez a különbség mondjuk 0<floor(np)< (ahol n lehet pozitív vagy negatív, de nem nulla). Ekkor vehetjük egyszerűen np többszöröseit, és ezek is (ahol n lehet pozitív vagy negatív, de nem nulla). Ekkor vehetjük egyszerűen np többszöröseit, és ezek is  sűrűek. sűrűek.
|
| Előzmény: [2915] jenei.attila, 2009-04-19 14:17:32 |
|
| [2916] lorantfy | 2009-04-19 15:08:06 |
 500. feladat: Egy bank páncélszekrényén 6 zár van. Kulcsaikat úgy osztották el a 4 pénztáros között, hogy a páncélszekrény kinyitásához legalább hármójuknak jelen kell lennie, de mind a négynek nem. Egy zárhoz többüknél is van kulcs, illetve egy pénztárosnál több kulcs is van. Hány olyan kulcselosztás van, melynél mindegyik pénztáros ugyanannyi kulccsal rendelkezik?
|
|
| [2915] jenei.attila | 2009-04-19 14:17:32 |
 Kíváncsian várom a te megoldásodat. Igazából ez a feladat hasonló állításra épül, mint amit az identitás fv. két periodikus fv. összegeként való előállításakor már említettem. Nevezetesen az np+kq alakú számok halmaza (ahol p,q rögzített nem összemérhető (p/q irracionális) számok, n és k pedig végigfutnak az egész számokon), sűrű a valós számok halmazában. Egyelőre úgy látom, hogy ezt a tényt a feladatod megoldásában ki kell használni, és ez az irracionális számok elsőrendűnél jobb racionális közelíthetőségén múlik.
|
| Előzmény: [2914] forex, 2009-04-19 10:32:27 |
|
|
|
|
|
| [2910] jenei.attila | 2009-04-15 13:07:10 |
 Először egy önmagában is érdekes segéd állítást fogok bebizonyítani: legyenek t valós, x irracionális, h pozitív valós számok adottak. Ekkor léteznek k és m természetes számok, hogy
|t+kx-m|<h
, vagyis a t kezdőértékű, x differenciájú számtani sorozat tagjai tetszőlegesen közel kerülhetnek egész számokhoz. Ismeretes, hogy az x irracionális szám másodrendben jól közelíthető racionális számokkal, ami azt jelenti, hogy végtelen sok a és b relatív prím természetes szám létezik, hogy
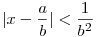
(az x irracionális szám lánctört kifejtésének szeletei ilyenek; ld. Niven Zuckerman: Bevezetés a számelméletbe). Válasszunk olyan b-t, amire 1/b<h/2 teljesül, u pedig definíció szerint legyen u:=[tb] ([] az egészrészt jelöli). Nyilván igaz, hogy 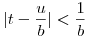 . Mivel a és b relatív prímek, létezik olyan 0 . Mivel a és b relatív prímek, létezik olyan 0 k<b természetes szám, amelyre b osztója u+ka -nak. Definíció szerint legyen k<b természetes szám, amelyre b osztója u+ka -nak. Definíció szerint legyen 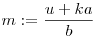 természetes szám. Ezek szerint természetes szám. Ezek szerint
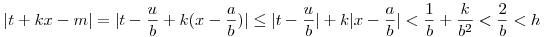
Visszatérve az eredeti feladathoz: tetszőleges n természetes számhoz olyan 2 hatványt kell találnunk, amelynek 10-es számrendszerbeli első néhány jegye éppen n-et adja. Ez azt jelenti, hogy léteznek k és m természetes számok, amelyekre
n10k 2m<(n+1)10k 2m<(n+1)10k
teljesül. Ezzel ekvivalens
log2n+k*log210 m<log2(n+1)+k*log210 m<log2(n+1)+k*log210
Látható, hogy az előző allításunkat kapjuk vissza 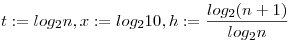 szereposztással, a k és m pedig ugyanaz. Itt a másodrendű racionális közelíthetőség miatt fontos, hogy log210 irracionális. Ezt szintén be kéne bizonyítani. szereposztással, a k és m pedig ugyanaz. Itt a másodrendű racionális közelíthetőség miatt fontos, hogy log210 irracionális. Ezt szintén be kéne bizonyítani.
|
| Előzmény: [2905] forex, 2009-04-04 14:42:56 |
|
| [2909] Cogito | 2009-04-14 16:28:10 |
 Szép, korrekt megoldás (egy apróság: alulról a 9. sorban a harmadik "=" helyére " " írandó). " írandó).
E feladat általánosítása kapcsán vetette fel Vasile Cirtoaje "egyenlőtlenség-szakértő" :) a következő tételt:
"Adottak az x1, x2, ..., xn nemnegatív valós számok, melyekre fennáll, hogy x1 + x2 + ... + xn = konstans1 és x12 + x22 + ... + xn2 = konstans2. Adott még a k > 2 szám.
Az S = x1k + x2k + ... + xnk összeg maximális, ha x1 = x2 = ... = xn-1  xn." xn."
E tétel bizonyítását 'Vasc' sajnos nem közölte. Ismeri valaki ezt a tételt? Érdekelne a bizonyítása, vagy legalább a forrásmű neve, elérhetősége.
|
| Előzmény: [2907] S.Ákos, 2009-04-11 22:33:02 |
|
|
|
| [2906] Cogito | 2009-04-11 20:52:35 |
 Az a, b, c nemnegatív valós számokra a + b + c = 3 és ab + bc + ca = 1. Határozzuk meg az a4 + b4 + c4 kifejezés maximumát.
|
|
| [2905] forex | 2009-04-04 14:42:56 |
 Sziasztok!
Bizonyítsátok be hogy tetszőleges k jegyű pozitív n egész számhoz létezik olyan kettőhatvány, melynek első k jegye rendre megegyezik n első k jegyével.
pl.: n=51 ----> 512 ; n=102 -----> 1024 ; n=20 ----> 2048 ;
|
|
|
| [2903] jenei.attila | 2009-04-04 09:08:53 |
 A jó sorozatokat következőképpen számoljuk össze: egy n hosszúságú jó sorozatban az előző n-1 elemből álló sorozat is jó. Jelöljük an-nel a nem fehér színnel végződő n hosszúságú jó sorozatok számát, bn-nel pedig a fehérrel végződők számát. Ekkor a jó sorozatok száma (amit cn-nel fogunk jelölni) nyilván cn=an+bn és a1=4 b1=1.
an=an-1+4bn-1
, mivel nem fehérre végződő jó sorozatot úgy kapunk, hogy az n-1 -edik elem nem fehér és akkor az n-edik elem ugyanolyan színű, vagy az n-1 -edik elem fehér de akkor az n-edik elem 4 féle színű lehet. Hasonlóan meggondolva
bn=an-1+bn-1
a fehérre végződő jó sorozatok száma annak megfelelően, hogy ekkor a megelőző n-1 hosszú jó sorozatot fehér színnel folytatjuk. Egy kis alakítással kapjuk: c1=5, c2=13
cn=2cn-1+3bn-1
(mivel cn=an+bn)
bn=cn-1
,amiből végül
cn=2cn-1+3cn-2
másodrendű lineáris rekurzió adódik. Meglehet adni zárt alakban is, ezt másra hagyom.
|
| Előzmény: [2894] gubanc, 2009-04-01 11:51:00 |
|
| [2902] jonas | 2009-04-02 19:25:54 |
 Ja értem. Én úgy próbáltam színezni a pontokat, hogy bármelyik két szomszédos vagy különböző színű legyen, vagy az egyik fehér. Te viszont azt mondtad, hogy bármelyik két szomszédos pont legyen vagy azonos színű, vagy az egyik közülük fehér.
Ebben az esetben a megfelelő sorozat szerintem az A046717 lesz.
|
| Előzmény: [2898] gubanc, 2009-04-01 20:22:57 |
|
| [2901] gubanc | 2009-04-02 16:27:50 |
 Látom, a legjobb úton haladsz a feladat általánosítása felé (Pl.: 5 szín helyett k szín ...). Csak dícsérni tudom ezt a kezdeményezést! :))
Előre is köszönet mindkettőtöknek, és az esetleges további hozzászólóknak is. (gubanc)
|
| Előzmény: [2900] BohnerGéza, 2009-04-02 15:19:38 |
|
|
| [2899] BohnerGéza | 2009-04-01 22:07:18 |
 Telhetetlen vagy gubanc!
(: Egy és két szín esetén tudnék segíteni. :)
(Sőt, egyelőre azt hiszem, három vagy több szín esetén lényegében ua. a feladat, esetleg a zárt alak megadásában lehetnek különböző nehézségűek. Azért megpróbálom komolyabban is.)
|
| Előzmény: [2894] gubanc, 2009-04-01 11:51:00 |
|
| [2898] gubanc | 2009-04-01 20:22:57 |
 Sajnos még mindig nem világos számomra a dolog. Hogyan érted azt, hogy "el kell tolni eggyel a sorozatot"? Azt láttuk, hogy a sorozat első tagjának 5-nek kell lennie. Ha ehhez igazodunk, akkor az OEIS-ből belinkelt sorozatot kettővel (és nem eggyel) eltolva a1 = 5 és a2 = 21 adódna. Így meg a2-vel van egy kis probléma ... . Egyébként javasolom, hogy lépjünk túl a rekurziós alakon és n  3-ra próbáljuk megadni (ha lehet) explicit módon is a sorozat n-edik tagját ( és persze előbb az a2 helyes számértékét). 3-ra próbáljuk megadni (ha lehet) explicit módon is a sorozat n-edik tagját ( és persze előbb az a2 helyes számértékét).
(Elnézést, ha valamit félreértettem volna.)
|
| Előzmény: [2897] jonas, 2009-04-01 19:00:06 |
|



 . Akkor a skatulya elv szerint ahogy írtad, léteznek i és j természetes számok, hogy {ix} és {jx} ugyanabba az 1/N hosszúságú részintervallumba esnek és különbözőek (mivel x irracionális). Ezért {ix}-{jx}<
. Akkor a skatulya elv szerint ahogy írtad, léteznek i és j természetes számok, hogy {ix} és {jx} ugyanabba az 1/N hosszúságú részintervallumba esnek és különbözőek (mivel x irracionális). Ezért {ix}-{jx}<

 k<b természetes szám, amelyre b osztója u+ka -nak. Definíció szerint legyen
k<b természetes szám, amelyre b osztója u+ka -nak. Definíció szerint legyen  " írandó).
" írandó). 


