| [2987] Lóczi Lajos | 2009-06-21 00:17:51 |
 Az asztroidot egy differenciálegyenlet megoldásaként is megkaphatjuk.
Ha f jelöli a keresett burkológörbét, akkor felírva az "érintőszakaszok pozitív síknegyedbe eső része konstans" feltételt, az alábbi egyenlet adódik:
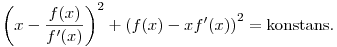
Ezt megoldva (és a triviális eseteket eldobva) éppen az asztroid egyenletét kapjuk.
|
| Előzmény: [2985] HoA, 2009-06-19 15:08:04 |
|
| [2986] leni536 | 2009-06-19 15:52:56 |
 Ennek a burkolónak a neve asztroid. Érdemes megfigyelni, hogy a buszok ajtaja is valahogy hasonlóan nyílik, és mivel az aljukon van egy seprű, ezért a lépcső alján lévő kosznak a burkolója is ugyanez a görbe.
|
|
|
|
| [2983] Alma | 2009-06-18 13:41:26 |
 Látom senki sem írta fel a polárkoordinátás megoldást, és újabb kérdések vetődtek fel, ezért beírom én.
Már az előttem szólók megállapították, hogy a mozgás során szimmetria okokból az eredeti négyzetalak megmarad, csak zsugorodik és elfordul. Jól jellemezhető a rendszer tehát két paraméterrel: az egyik pont középponttól (ez lesz az origó) való r távolságával, ami kezdetben 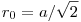 , valamint az origóból a pontba mutató vektor , valamint az origóból a pontba mutató vektor  szögelfordulásával. szögelfordulásával.
Minden pillanatban a pontok sebességvektorának radiális és tangenciális komponense is 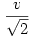 , ami azt jelenti, hogy a következő differenciálegyenleteket írhatjuk fel a sebesség definíciója alapján: , ami azt jelenti, hogy a következő differenciálegyenleteket írhatjuk fel a sebesség definíciója alapján: 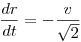 valamint valamint 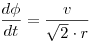 . Az első egyenlet megoldása kezdeti feltétellel: . Az első egyenlet megoldása kezdeti feltétellel:
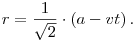
Ebből leolvasható, hogy a pontok 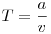 idő mulva találkoznak, vagyis addig a utat tesznek meg. idő mulva találkoznak, vagyis addig a utat tesznek meg.
Ha már eddig leírtam, akkor gyorsan a pályát is levezetem ebből:
A kapott sugár-idő függvényt behelyettesítve a szögre vonatkozó differenciálegyenletre a következőt kapjuk:
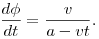
Integrálva az egyenletet, valamint figyelembe véve a kezdeti feltételt 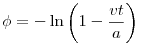 . Az időt kifejezve a pillanatnyi sugárral és behelyettesítve ide megkapjuk a pálya egyenletét: . Az időt kifejezve a pillanatnyi sugárral és behelyettesítve ide megkapjuk a pálya egyenletét:
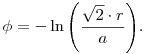
Kicsit szebb alakban:
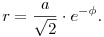
Ez pedig egy logaritmikus spirál.
|
| Előzmény: [2979] Lóczi Lajos, 2009-06-17 22:49:08 |
|
|
|
| [2980] HoA | 2009-06-18 09:53:57 |
 Látszik. Érdemes megfigyelni , hogy [2961] ábráján hogyan változik az időközben teknőcökké előlépett pontok által alkotott négyzet oldalhossza, ha azok  x -et lépnek egymás felé. Különösen hasznos ezt összevetni a [2972]-ben említett háromszöges változat esetével. Szabatos-e az ezekből levezetett eredmény a görbe hosszára azon az alapon, hogy mikorra csökken a futópontok által meghatározott négyzet/háromszög oldalhossza 0-ra? x -et lépnek egymás felé. Különösen hasznos ezt összevetni a [2972]-ben említett háromszöges változat esetével. Szabatos-e az ezekből levezetett eredmény a görbe hosszára azon az alapon, hogy mikorra csökken a futópontok által meghatározott négyzet/háromszög oldalhossza 0-ra?
|
| Előzmény: [2979] Lóczi Lajos, 2009-06-17 22:49:08 |
|
|
|
| [2977] HoA | 2009-06-17 20:20:02 |
 Egy "kapcsolódási pont": Az ábra szimmetrikus az y=x egyenesre, így a keresett függvény saját inverze. Ellenőrizhetjük Ákos megoldását:
y=(1-x2/3)3/2
y2/3=1-x2/3
x2/3=1-y2/3
x=(1-y2/3)3/2
A megoldás tehát akár jó is lehet :-)
|
| Előzmény: [2976] Lóczi Lajos, 2009-06-17 15:33:27 |
|
| [2976] Lóczi Lajos | 2009-06-17 15:33:27 |
 (Persze az egységlétra esetén :)
A feladatot még többféleképp is meg lehet oldani, bizonyára látni fogunk több szép geometriai, illetve differenciálegyenletes kapcsolódási pontot.
|
| Előzmény: [2975] S.Ákos, 2009-06-17 14:47:38 |
|
|
|
| [2973] Lóczi Lajos | 2009-06-17 12:16:38 |
 Itt egy másik rokon klasszikus feladat.
Egy falhoz támasztott létra az ábrán látható módon lecsúszik. (A létra két vége tehát mindig érinti a falat, illetve a padlót.) Írjuk fel az így kialakult burkológörbét.
|
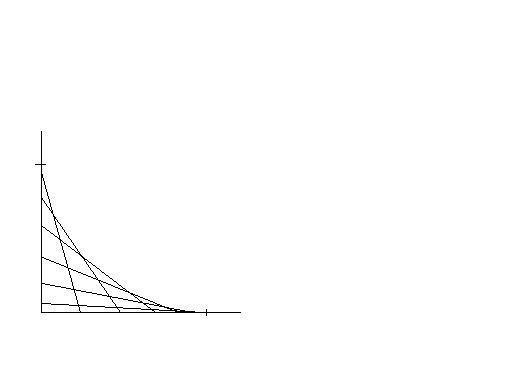 |
|
| [2972] Alma | 2009-06-17 03:19:46 |
 A feladathoz annyit fűznék hozzá, hogy ez fizikus körökben egy nagyon ismert feladat (illetve ennek a háromszöges verziója, mely lényegében ugyanez). Középiskolai módszerekkel jól tárgyalható, nem kellenek komplex számok sem hozzá. A feladaton keresztül be lehet vezetni a polárkoordinátákat, mert messze célravezetőbb használatuk ebben az esetben, mint a Descartes-koordinátáké. Polárkoordinátákban gondolkodva lényegében 3-4 sor a feladat megoldása.
|
| Előzmény: [2961] Lóczi Lajos, 2009-06-16 00:07:09 |
|
|
| [2970] Tibixe | 2009-06-16 22:23:33 |
 Vegyük fel az ábrát a komplex számsíkon, úgy hogy a négyzet középpontja a 0 pont legyen.
Egy kiválasztott teknős pályáját írja le az F(t) függvény, ahol t egy valós paraméter (pl. idő).
Szimmetriaokokból a következő teknős helye a kiválasztott teknős helye 90o-kal elforgatva, azaz i-vel szorozva.
Fk(t)=iF(t)
A teknős sebességének iránya mindig a következő felé mutat, a nagysága a feladat szempontjából lényegtelen, most válasszuk meg kényelmesen.
F'(t)=Fk(t)-F(t)
azaz
F'(t)=iF(t)-F(t)
F'(t)=(i-1)F(t)
Ez egy pofonegyszerű differenciálegyenlet, a megoldásai pedig:
F(t)= e(i-1)t e(i-1)t
alakúak, ahol  tetszőleges komplex szám. tetszőleges komplex szám.
Ha például azt akarjuk, hogy a kiválasztott teknős t=0-nál az (1;1) pontban legyen, akkor
 =1+i =1+i
kell nekünk.
Ezzel nem csak négyzetre, hanem más szabályos n-sokszögekre is fel lehet írni a pályát:
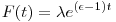
ahol  egy megfelelő n-edik egységgyök. egy megfelelő n-edik egységgyök.
F(t) alakjából látszik, hogy a megoldás logaritmikus spirál lesz, amely az origóba tart.
|
| Előzmény: [2969] HoA, 2009-06-16 21:21:39 |
|
| [2969] HoA | 2009-06-16 21:21:39 |
 Szimmetria okokból a négy pont mindig egy négyzet csúcsaiban helyezkedik el és e négyzetek középpontja közös ( O ) . A pályák érintője kezdetben 45oos szöget zár be az O -ból a görbe pontjába mutató vektorral. A pontnégyes bármelyik későbbi helyzetét is tekinthetjük a további mozgás kiindulópontjának, így ez a tulajdonság a pályák további pontjaira is igaz. A négy pálya tehát négy olyan görbe, melynek minden P pontjára az OP helyvektor 45o -os szöget zár be a P-beli érintővel. A logaritmikus spirálok egyenletének felírását meghagyom a következő hozzászólónak.
|
| Előzmény: [2961] Lóczi Lajos, 2009-06-16 00:07:09 |
|
|
|
|
| [2965] nadorp | 2009-06-16 12:14:11 |
 Ezt a kérdést most nem értem. A rekurzióból látszik, hogy a sorozatot az első elem egyértelműen meghatározza, másrészt "adja magát", hogy generátor függvényt használjunk és hogy ennek a négyzetét kell vizsgálni ( "látszik", hogy a rekurzió két polinom szorzatában az n+1-ed fokú tag együtthatóját tartalmazza).
|
| Előzmény: [2962] Lóczi Lajos, 2009-06-16 00:08:23 |
|
| [2964] sakkmath | 2009-06-16 11:04:40 |
 Csatlakozom rizseszhez annyiban, hogy érdemes pontosítani a szöveget a triviális esetek kiküszöbölése céljából.
Közölni kellene azt, hogy a "szomszéd" a csúcsok mely körüljárási iránya szerint értendő. Ha a rajz a feladat eredeti szövegéhez készült, akkor (a mi nézőpontunkból) az óramutató járásával ellentétes irányt kell még megadni.
|
| Előzmény: [2961] Lóczi Lajos, 2009-06-16 00:07:09 |
|
|





 ;BT=cos2
;BT=cos2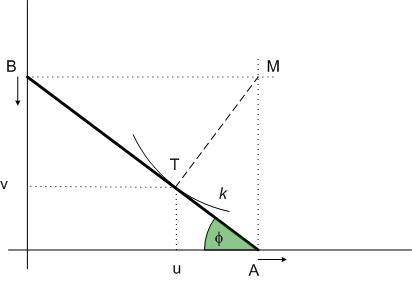





 x0). A derivált és második derivált vizsgálatából következik, hogy
x0). A derivált és második derivált vizsgálatából következik, hogy 


 e(i-1)t
e(i-1)t egy megfelelő n-edik egységgyök.
egy megfelelő n-edik egységgyök. 