| [3089] bily71 | 2009-11-30 23:59:25 |
 Ezek pedig nem csupa páros pithagoraszi számhármasok, miért következne abból, hogy m=2|a, hogy mind páros? Már félek bármit is írni, annyira szigorúan bántok velem...
|
| Előzmény: [3088] bily71, 2009-11-30 23:52:21 |
|
| [3088] bily71 | 2009-11-30 23:52:21 |
 Legyen m=2,a=4,x=1,n=1, ekkor
am+(n+mx)m=(n+a)m
42+(1+(2.1)2=(1+4)2,
vagy m=2,a=12,x=2,n=1, ekkor
122+(1+2.2)2=(1+12)2.
Tehát m=2, és igaz! Én erre gondoltam.
|
| Előzmény: [3087] bily71, 2009-11-30 23:38:47 |
|
| [3087] bily71 | 2009-11-30 23:38:47 |
 Tehát a következő gondolatmenet hamis állításokból áll?
am+(n+mx)m=(n+a)m
(n+a)m nm(mod a) nm(mod a)
am+(n+mx)m (n+mx)m(mod a) (n+mx)m(mod a)
(n+mx)m nm(mod a) nm(mod a)
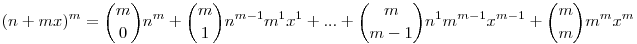
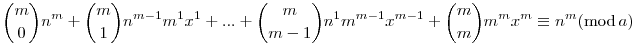
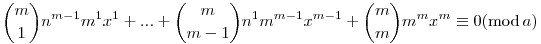
A bal oldali összeg minden tagja osztható m-el, és az összeg a-val osztva 0-át ad maradékul, ebből nem következik, hogy m|a? És ha nem, akkor miért?
|
| Előzmény: [3085] SAMBUCA, 2009-11-30 21:08:02 |
|
| [3086] rizsesz | 2009-11-30 23:00:07 |
 kedves bily71. ilyenkor alapjaiban remeg meg az a hite az embernek, hogy van bármiféle közöd a matematikához.
hogy lehet egy ilyen kérdést feltenni úgy, hogy tudod, hogy sosem igaz az adott állítás? :(
|
| Előzmény: [3083] bily71, 2009-11-30 20:28:42 |
|
|
|
|
| [3082] SmallPotato | 2009-11-30 20:14:27 |
 Legyen n páratlan; ekkor van olyan összekötő szakasz, amely a négyzet oldalaival 45°-os szöget zár be és a származtatás (BD-re vonatkozó) szimmetriája miatt E-ben érinti a szóban forgó burkológörbét. Ha ez a szakasz AB-n az A ponttól a k-adik osztópontból indul, akkor a a másik végpontja a származtatás értelmében BC-n a B-től a k+1-edik osztópont. A 45° miatt viszont ez C-től a k-adik osztópont. A BC szakasz két darabjából tehát 2k+1=n. Ha mármost n a végtelenhez tart, akkor 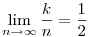 , tehát a jelzett szakasz határhelyzetben AB és BC felezőpontjait köti össze. Az E pont ezek szerint negyedeli a BD átlót. , tehát a jelzett szakasz határhelyzetben AB és BC felezőpontjait köti össze. Az E pont ezek szerint negyedeli a BD átlót.
|
| Előzmény: [3075] bily71, 2009-11-29 18:21:36 |
|
|
|
|
|
|
|
| [3075] bily71 | 2009-11-29 18:21:36 |
 Adott az ABCD négyzet. Osszuk fel az AB és a BC oldalakat n egyenlő részre. Kössük össze az A csúcsot a BC oldal B-hez közelebbi első osztópontjával, azután az AB oldal A-hoz közelebbi első osztópontját a BC oldal B-hez közelebbi második osztópontjával, sít., végül az AB oldal B-hez közelebbi első osztópontját fogjuk összekötni a C csúccsal. A kapott szakaszok egy görbét érintenek, ami az E pontban metszi a BD átlót. Milyen arányban osztja az E pont az átlót, ha n-et minden határon túl növeljük?
|
|
| [3074] Janosov Milán | 2009-11-29 17:27:54 |
 Hahó!
Egy szerintem érdekes (de nem annyira nehéz feladat):
Írjuk fel a 24-et az 1, 3, 4 és 6 számok és az alapműveletek segítségével úgy, hogy mindegyik számot pontosan egyszer kell felhasználni, zárójelet használhatunk, de a számokat közvetlenül egymás mellé írva többjegyű számokat alkotni nem szabad.
(A feladat egy BME-s felvételivel kapcsolatos újságjából való)
|
|
|
|
|
| [3070] bily71 | 2009-11-29 10:07:49 |
 Nem fokozom, csak leírom a választ.
am+bm=cm, mivel c>a, létezik n egész, hogy c=a+n. Fermat tételéből következik, mivel m prím, hogy
cm c c (a+n)m (a+n)m a+n(mod m) a+n(mod m)
, továbbá
am a(mod m) a(mod m)
bm b(mod m) b(mod m)
, ebből
am+bm a+b a+b a+n(mod m) a+n(mod m)
b n(mod m) n(mod m)
, tehát
b=n+xm
, ahol x nemnegatív egész.
|
| Előzmény: [3067] bily71, 2009-11-28 16:05:53 |
|
|
|
|
|
| [3063] bily71 | 2009-11-27 22:41:08 |
 Igaz-e, hogy ha teljesül az am+bm=cm egyenlőség, akkor teljesül az am+(n+mx)m=(a+n)m egyenlőség is, ahol b=n+mx, c=a+n?
(a<b<c és a,b,c,n,m,x nemnegatív egészek.)
|
|



 nm(mod a)
nm(mod a)

 2, akkor én vagyok a római pápa."
2, akkor én vagyok a római pápa."


