| [3103] Lóczi Lajos | 2009-12-13 01:15:16 |
 Következzen végül néhány újabb kérdés és sejtés a C függvény kapcsán, amelyek természetes módon felmerülnek és amelyek között szerintem nehezebbek is vannak. (A saját tippjeimet egyelőre nem írom ide, hogy ne befolyásoljak senkit.)
Egy n szám 2-es ciklus, ha C(n) n, de C(C(n))=n. Hasonlóan definálhatók a k-hosszú ciklusok is. n, de C(C(n))=n. Hasonlóan definálhatók a k-hosszú ciklusok is.
3. feladat. Melyik az a legkisebb n, amely (a C leképezés iterációja során) előbb-utóbb 2-es ciklust eredményez?
4. feladat. Melyik az a legkisebb n, amely rögtön egy 2-es ciklus egyik tagja?
5. feladat. Igaz-e, hogy minden kezdőértékre a C iteráltjaiból alkotott sorozat előbb-utóbb ciklikussá válik? Ha igen, van-e tetszőlegesen hosszú "átmeneti szakasz", mielőtt a sorozat ciklizálni kezd? Van-e maximális ciklushossz, vagy pedig tetszőlegesen hosszú ciklusok előfordulhatnak?
6. feladat. Igaz-e, hogy C-nek van legnagyobb fixpontja? Ha igen, konkrétan melyik szám az?
A fenti C leképezést egyébként a Conway-féle "look and say" sorozat mintájára gyártottam, csak annál egyszerűbb. A Conway-féle sorozat sok érdekes tulajdonsággal bír, különösen meghökkentő a rá vonatkozó "cosmological theorem".
|
| Előzmény: [3096] Lóczi Lajos, 2009-12-12 11:16:37 |
|
| [3102] Radián | 2009-12-12 19:41:48 |
 Ha vesszük a hatjegyűeket, ott 3 db különböző számjegy kell szerepeljen. A szám mindegy jegye kisebb az 5-nél. Ha a számok C(n) alakját akarom felírni az alábbi esetek állhatnak fenn:
1.) 4db x 1db y 1db z (a 4-es és 2 db 1-es sorrendje persze más is lehet, 1,4,1 1,1,4.) Tehát a számban biztosan fog szerepelni az 1,4,q számjegyek. 1-esből biztosan kell legyen legalább 2 db a C(n) felírás alapján, így a számban csak 4 db 1-es fordulhat elő, de ekkor nem az 1. ponti lenne a C(n) alak.
2.) 2db x 2db y 2db z Az 1. ponthoz hasonlóan n kellene tartalmazzon 3 db 2-est ,azaz C(n) alakjába kellene legyen egy 3db q alakú rész. Tehát ez az eset sem állhat elő.
3.) 1db x 2db y 3db z (Az 1,2,3 sorrendje más is lehet.) A szám eredeti alakjába tehát kell szerepeljen 1-es 2-es és 3-as, ezzel meg van az összes különböző jegy. Mivel x,y,z nem egyenlő egymással, így 1-esből 2-esből és 3-masból is több mint egy jegy fog szerepelni a számban, tehát nem lehet a C(n) alakja a 3. pontbeli.
|
| Előzmény: [3101] Radián, 2009-12-12 19:17:27 |
|
| [3101] Radián | 2009-12-12 19:17:27 |
 A négyjegyűeket átfutottam. Egyik se lett jó. Elvileg csak a hatjegyűek között akadhat kisebb, de ezeket nem néztem meg rendesen. 4 jegyűeknél a szám pontosan két különböző számjegyet kell tartalmazzon, ráadásul mindkét jegyből 2-2 db van. E jegyek pedig a 0,1,2 közül kerülhetnek ki. Mivel mindkét jegyből 2-2 db van, ezért a keresett számok csak 2x2x alakúak lehetnek melyek nyilván nem egyenlők a hozzájuk rendelhető C(2x2x)-szel.
|
| Előzmény: [3099] Valezius, 2009-12-12 18:07:21 |
|
| [3100] Sirpi | 2009-12-12 18:17:40 |
 5 perc alatt összeütöttem rá egy progit, amiből kiderült, hogy ez-e a 2. legkisebb... Annyit mindenesetre elárulok, hogy legfeljebb 8 jegyű megoldás 36 db van.
|
| Előzmény: [3099] Valezius, 2009-12-12 18:07:21 |
|
| [3099] Valezius | 2009-12-12 18:07:21 |
 Ha 8 jegyűt keresünk, akkor 10-val kell kezdődnie, a 3. jegy 0,1,2 lehet, amiből a 0 nem lehet, de az 1 sem, hisz ez a helyiérték az egyesek számát mutatja. 1021x2yz alakú számok maradtak. x legalább 3. És ekkor kijön, amit írtál. Amiről elhiszem, hogy kisebb, mint az enyém :) Tehát ha van kisebb, akkor az 4 vagy 6 jegyű lehet.
|
| Előzmény: [3098] Radián, 2009-12-12 16:12:24 |
|
|
|
| [3096] Lóczi Lajos | 2009-12-12 11:16:37 |
 Vezessük be a következő, C-vel jelölt függvényt.
C egy tízes számrendszerbeli pozitív egészhez egy ugyanilyen típusú számot rendel. A számok nem kezdődhetnek 0-val.
Ha n egy pozitív egész, akkor C(n) értéke legyen az a szám, amelyet úgy kapunk, hogy számjegyenként nagyság szerint sorban megszámoljuk, hogy az illető jegyből az n szám összesen hány darabot tartalmaz, ezt leírjuk, majd rögtön utána hozzáírjuk a számjegyet magát, és ezt minden szereplő jegyre megismételjük folytatólagosan leírva.
Például C(2009)=201219, mert 2009-ben (számjegyek szerint növekvő sorrendben) található "2 darab 0", "1 darab 2-es" és "1 darab 9-es".
Egy másik példa: C(31415927)=21121314151719.
Ha valamely számjegy nem szerepel n-ben, azt C nem veszi figyelembe, tehát nem mondunk olyat, hogy pl. "nulla darab egyes".
Egy n szám a C függvénynek fixpontja, ha C(n)=n.
1. feladat: Keressük meg C legkisebb fixpontját.
2. feladat: Keressük meg C második legkisebb fixpontját.
|
|
| [3095] bily71 | 2009-12-02 11:59:04 |
 Valószínűleg megbuktatnának :) Nem okoskodok tovább, igazatok van, inkább sokak örömére visszavonulok, nagyon keveset tudok, én itt esetleg csak kérdezhetek, ide nem elég a matek szeretete, itt tényleg zsenik vannak, valóban ez nem az a fórum... Inkább ezt a pár hónapot a felvételire való felkészüléssel kellene töltenem, elvégre sok bepótolni valóm van.
|
| Előzmény: [3094] nadorp, 2009-12-02 08:52:48 |
|
| [3094] nadorp | 2009-12-02 08:52:48 |
 Nem tudom mit szólnának hozzá egy számelmélet vizsgán
"...ergó n|mx, mivel m prím, ezért n|x"
1) ha 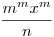 egész, akkor csak az következik, hogy n|mmxm. Az állításod első fele csak akkor igaz ha n prím ( 12|33.143, de 12 egész, akkor csak az következik, hogy n|mmxm. Az állításod első fele csak akkor igaz ha n prím ( 12|33.143, de 12|3.14)
2) 18|3.30, mivel 3 prím ezért 18|30 ?????????????
|
| Előzmény: [3092] bily71, 2009-12-01 12:02:44 |
|
| [3093] bily71 | 2009-12-01 14:21:22 |
 Persze abból, hogy n|x, még nem következik, hogy m|a, csak érdekesnek találtam, így leírtam. Egyébként, ha m=2, akkor igaz minden esetben, hogy 2|a, mivel a és b közül az egyik páros, és igazából nincs jelentősége annak, hogy a két négyzetszám közül, amelyek összege is négyzetszám, melyiket jelöljük a-val, jelölhetjük mindig a párosat.
|
| Előzmény: [3092] bily71, 2009-12-01 12:02:44 |
|
| [3092] bily71 | 2009-12-01 12:02:44 |
 Folytatva:
am+(n+mx)m=(n+a)m
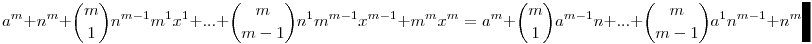
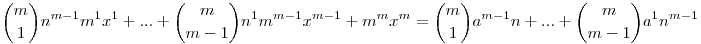
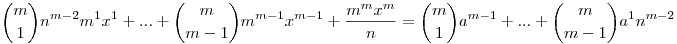
A jobb oldali tört elötti, és a bal oldali összeg értéke egész, ebből következik, hogy a tört értéke is egész, ergó n|mx, mivel m prím, ezért n|x. Tehát
am+(n(my+1))m=(n+a)m
|
| Előzmény: [3087] bily71, 2009-11-30 23:38:47 |
|
| [3089] bily71 | 2009-11-30 23:59:25 |
 Ezek pedig nem csupa páros pithagoraszi számhármasok, miért következne abból, hogy m=2|a, hogy mind páros? Már félek bármit is írni, annyira szigorúan bántok velem...
|
| Előzmény: [3088] bily71, 2009-11-30 23:52:21 |
|
| [3088] bily71 | 2009-11-30 23:52:21 |
 Legyen m=2,a=4,x=1,n=1, ekkor
am+(n+mx)m=(n+a)m
42+(1+(2.1)2=(1+4)2,
vagy m=2,a=12,x=2,n=1, ekkor
122+(1+2.2)2=(1+12)2.
Tehát m=2, és igaz! Én erre gondoltam.
|
| Előzmény: [3087] bily71, 2009-11-30 23:38:47 |
|
| [3087] bily71 | 2009-11-30 23:38:47 |
 Tehát a következő gondolatmenet hamis állításokból áll?
am+(n+mx)m=(n+a)m
(n+a)m nm(mod a) nm(mod a)
am+(n+mx)m (n+mx)m(mod a) (n+mx)m(mod a)
(n+mx)m nm(mod a) nm(mod a)
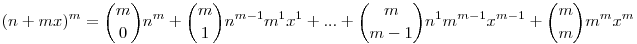
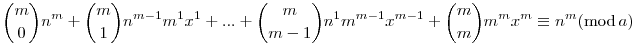
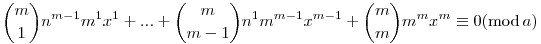
A bal oldali összeg minden tagja osztható m-el, és az összeg a-val osztva 0-át ad maradékul, ebből nem következik, hogy m|a? És ha nem, akkor miért?
|
| Előzmény: [3085] SAMBUCA, 2009-11-30 21:08:02 |
|
| [3086] rizsesz | 2009-11-30 23:00:07 |
 kedves bily71. ilyenkor alapjaiban remeg meg az a hite az embernek, hogy van bármiféle közöd a matematikához.
hogy lehet egy ilyen kérdést feltenni úgy, hogy tudod, hogy sosem igaz az adott állítás? :(
|
| Előzmény: [3083] bily71, 2009-11-30 20:28:42 |
|
|
|
|
| [3082] SmallPotato | 2009-11-30 20:14:27 |
 Legyen n páratlan; ekkor van olyan összekötő szakasz, amely a négyzet oldalaival 45°-os szöget zár be és a származtatás (BD-re vonatkozó) szimmetriája miatt E-ben érinti a szóban forgó burkológörbét. Ha ez a szakasz AB-n az A ponttól a k-adik osztópontból indul, akkor a a másik végpontja a származtatás értelmében BC-n a B-től a k+1-edik osztópont. A 45° miatt viszont ez C-től a k-adik osztópont. A BC szakasz két darabjából tehát 2k+1=n. Ha mármost n a végtelenhez tart, akkor 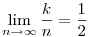 , tehát a jelzett szakasz határhelyzetben AB és BC felezőpontjait köti össze. Az E pont ezek szerint negyedeli a BD átlót. , tehát a jelzett szakasz határhelyzetben AB és BC felezőpontjait köti össze. Az E pont ezek szerint negyedeli a BD átlót.
|
| Előzmény: [3075] bily71, 2009-11-29 18:21:36 |
|
|
|
|
|
|



 n, de C(C(n))=n. Hasonlóan definálhatók a k-hosszú ciklusok is.
n, de C(C(n))=n. Hasonlóan definálhatók a k-hosszú ciklusok is. 


 nm(mod a)
nm(mod a)


