|
|
|
| [3201] sakkmath | 2010-02-05 15:18:09 |
 Lehet, hogy ez túlságosan ismert feladat, ezért beírom a következőt is, amely a Nehezebb matematikai problémák /[652]-ben már szerepelt, de azóta sem érkezett rá teljes értékű megoldás:
Legyen  , ahol 0 , ahol 0 x x y y z és z és   0. Határozzuk meg az 0. Határozzuk meg az  paraméter értékét úgy, hogy paraméter értékét úgy, hogy
a) f(x, y, z) 0, 0,
b) f(x, y, z) 0 0
teljesüljön.
|
| Előzmény: [3200] sakkmath, 2010-02-04 16:40:13 |
|
|
|
|
| [3196] m2mm | 2010-02-02 17:15:01 |
 Szép megoldás, enyémnél biztosan szebb. Egy egy fokkal nehezebb:
Bizonyítsuk be, hogy ha a,b,c valós számok, akkor
a4+b4+c4+3(a2b2+b2c2+c2a2) 2(a3b+b3c+c3a+ab3+bc3+ca3) 2(a3b+b3c+c3a+ab3+bc3+ca3)
|
| Előzmény: [3193] sakkmath, 2010-02-02 13:59:56 |
|
|
| [3194] bily71 | 2010-02-02 14:06:58 |
 Ha nem, hát nem.
Átnézem mégegyszer, hogy rájöjjek, hol hibáztam. Egyébként nem az n=1 behelyettesítésre gondoltam. [3185]-ben megadtam egy rekurzív eljárást: i! aij(mod p), ahol j aij(mod p), ahol j (i-1)!mod p). Nekem hirtelen úgy tűnt, hogy a rekurzió miatt (p-1)!-nek nincs más lehetősége, mint kongruensnek lenni p-1-gyel modulo p. (i-1)!mod p). Nekem hirtelen úgy tűnt, hogy a rekurzió miatt (p-1)!-nek nincs más lehetősége, mint kongruensnek lenni p-1-gyel modulo p.
Lehet, hogy lefelejtettem egy felkiáltójelet?:)
|
| Előzmény: [3188] m2mm, 2010-02-01 21:13:36 |
|
| [3193] sakkmath | 2010-02-02 13:59:56 |
 0 (a+b-c)2(a-b)2+(b+c-a)2(b-c)2+(c+a-b)2(c-a)2= (a+b-c)2(a-b)2+(b+c-a)2(b-c)2+(c+a-b)2(c-a)2=
=2(ab2c+abc2+a2bc+a4+b4+c4-a3b-a3c-ab3-ac3-b3c-bc3).
2-vel elosztjuk az egyenlőtlenséget, majd jobb oldalon az első három tagból kiemelünk abc-vel és kapjuk:
0 abc(a+b+c)+a4+b4+c4-(a3b+a3c+ab3+ac3+b3c+bc3). Az abc=1 behelyettesítése után a kívánt egyenlőtlenség adódik. Végig azonos átalakításokat alkalmaztunk. abc(a+b+c)+a4+b4+c4-(a3b+a3c+ab3+ac3+b3c+bc3). Az abc=1 behelyettesítése után a kívánt egyenlőtlenség adódik. Végig azonos átalakításokat alkalmaztunk.
|
| Előzmény: [3189] m2mm, 2010-02-01 21:32:17 |
|
| [3192] Róbert Gida | 2010-02-02 00:10:01 |
 Igen, de én nem írtam olyanokat, hogy "igazán komoly tételem", sőt azt írtam az én feladatomra, hogy "Ezt könnyű igazolni". De valóban írhattad volna rá, hogy halálismert, az sem zavart volna.
"Nem ugattalak le, pedig én utána érdemben(!) hozzá tudtam szólni a dologhoz (ez most rólad nem mondható el)."
Ja, kb. 18 éve megvan Szalay Mihály számelmélet könyve ( 7 forintba került) Shapiro karakteres bizonyításával. Erre is mondhatnám, hogy halálismert.
|
| Előzmény: [3190] Maga Péter, 2010-02-01 21:37:30 |
|
|
| [3190] Maga Péter | 2010-02-01 21:37:30 |
 1. Sokat téptem a számat a Goldbach-topikon (meg hát mások is), most bily testhezálló dolgot csinált, végre rendesen. Amikor hülyeséget csinált, leszóltuk érte. Most nem csinál hülyeséget, ha ezért is leszóljuk, akkor azt fogja gondolni, hogy igazából mindegy, hogy mit csinál.
2. Amikor te a Goldbach-topikban megtetted a hozzászólást, ami szerint a Dirichletben nem a végtelen sok, hanem a legalább 1 prím a nehéz, akkor arra nem azt írtam, hogy ez halálismert. Nem ugattalak le, pedig én utána érdemben(!) hozzá tudtam szólni a dologhoz (ez most rólad nem mondható el).
3. Ha a gyereked beszélni tanul, gügyögésért ne vágd szájon. Valóban nem gügyögve kell beszélni, de didaktikailag messze nem optimális megoldás a szájonvágás.
|
| Előzmény: [3182] Róbert Gida, 2010-02-01 11:43:16 |
|
| [3189] m2mm | 2010-02-01 21:32:17 |
 Remélem még nem volt, és igaz(saját alkotás): a,b,c valós számokra abc=1. Bizonyítsuk be, hogy a4+b4+c4+a+b+c a3b+b3c+c3a+ab3+bc3+ca3. Ha közismert lenne, akkor elnézést. a3b+b3c+c3a+ab3+bc3+ca3. Ha közismert lenne, akkor elnézést.
|
|
|
| [3187] bily71 | 2010-02-01 20:03:10 |
 Bármely n számrendszerbeli szorzótábla, (tehát nemcsak prím) ha elhagyjuk a 0-át, mint szorzótényezőt, középontosan szimmetrikus, hiszen
ab (n-a)(n-b) (n-a)(n-b) (mod n). (mod n).
Ugyanezen táblázat tengelyesen is szimmetrikus, a maradékok abszolútértékére tekintettel, hiszen
|ab| |(n-a)b| |(n-a)b| |a(n-b)|(mod n). |a(n-b)|(mod n).
Ez nem fontos, de, ha már szóba került: ha a szorzótábla p, azaz prím számrendszerbeli, akkor az a szám csak egyszer fordulhat elő soronként, ugyanis, ha többször szerepelne, akkor vagy a|p, vagy (a,p) 1, egyik sem lehetséges, hiszen p prím, tehát a táblázat latin négyzet. 1, egyik sem lehetséges, hiszen p prím, tehát a táblázat latin négyzet.
Ezen tulajdonságokat immáron bizonyítottnak tekinthetjük.
Most már nincs több teendőnk, csak a behelyettesítéseket kell végrehajtani a
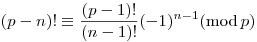
képletbe, és az eredmény a Wilson-tétel.
Egyébként szó sincs arról, hogy ki kellene számolni (n-1)! értékét, vagyis, hogy n-2 darab szorzást kellene eszközölni egy szám Wilson-féle tesztelése során. Legyen 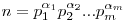 . Legyen k=pi . Legyen k=pi i, azaz a prímek kitevőjükkel vett szorzatok közül a legnagyobb. Ekkor i, azaz a prímek kitevőjükkel vett szorzatok közül a legnagyobb. Ekkor
k! 0(mod n). 0(mod n).
Tehát elég k darab szorzást és k darab osztást, azaz 2k darab műveletet végrehajtani.
De az is lehet, hogy szokás szerint tévedtem, ez esetben elnézést kérek mindenkitől.
|
| Előzmény: [3186] Róbert Gida, 2010-02-01 17:11:09 |
|
| [3186] Róbert Gida | 2010-02-01 17:11:09 |
 "Az előbb felsorolt tulajdonságok ismertek, bizonyításukat most mellőzhetjük."
Életemben nem hallottam, hogy valaki is latin négyzetekkel próbálná bebizonyítani a Wilson tételt. Ne tartsd magadban!
|
| Előzmény: [3185] bily71, 2010-02-01 15:41:23 |
|
| [3185] bily71 | 2010-02-01 15:41:23 |
 Wilson szerint (p-1)! p-1(mod p), ha p prím. p-1(mod p), ha p prím.
Tekintsük a p számrendszerbeli szorzótáblát. Ha a 0-át kihagyjuk, azaz a számokat csak 1-től p-1-ig szorozzuk össze, akkor a táblázat i-edik oszlopának j-edik eleme aij i.j(mod p). i.j(mod p).
Ebből következik, hogy i! aij(mod p), ahol j aij(mod p), ahol j (i-1)!(mod p). (i-1)!(mod p).
A táblázat, mivel p prím, egy latin négyzet, amely nem tartalmazza a 0-át és középpontosan szimmetrikus, azaz aij a(p-i)(p-j)(mod p), továbbá tengelyesen is szimmetrikus oly módon, hogy aij a(p-i)(p-j)(mod p), továbbá tengelyesen is szimmetrikus oly módon, hogy aij p-a(p-i)j(mod p). Az előbb felsorolt tulajdonságok ismertek, bizonyításukat most mellőzhetjük. p-a(p-i)j(mod p). Az előbb felsorolt tulajdonságok ismertek, bizonyításukat most mellőzhetjük.
A fenti szimmetriákból és a 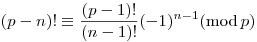 összefüggésből adódik, hogy (p-1)! összefüggésből adódik, hogy (p-1)! p-1(mod p), tehát ez egy speciális eset. p-1(mod p), tehát ez egy speciális eset.
|
| Előzmény: [3184] Fálesz Mihály, 2010-02-01 12:04:48 |
|
| [3184] Fálesz Mihály | 2010-02-01 12:04:48 |
 Úgy látom, kezdenek forrósodni a kedélyek...
Szóval,
(p-1)!=(p-n)!.(p-n+1)(p-n+2)...(p-1) (p-n)!.(-n+1)(-n+2)...(-1)=(p-n)!.(-1)n-1(n-1)! (mod p), (p-n)!.(-n+1)(-n+2)...(-1)=(p-n)!.(-1)n-1(n-1)! (mod p),
és persze egyszerűsíthetünk bármivel, ami nem osztható p-vel.
De hol van ebben a Wilson-tétel?
|
|
|
| [3182] Róbert Gida | 2010-02-01 11:43:16 |
 Halál ismert példa, k=n-1 jelöléssel és osztással azt állítja a feladat, hogy 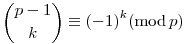 . Ami például Graham Konkrét matematika című könyvében az 5. fejezet 5. példája. És szerinte ez k=0-ra spec. esete a Wilson tételnek. Egy túróst. . Ami például Graham Konkrét matematika című könyvében az 5. fejezet 5. példája. És szerinte ez k=0-ra spec. esete a Wilson tételnek. Egy túróst.
|
| Előzmény: [3179] Maga Péter, 2010-02-01 08:11:25 |
|
| [3181] bily71 | 2010-02-01 09:43:04 |
 Saját! Ez az első "igazán komoly tételem", amit bizonyítanom is sikerült.:)
Ezzel a képlettel felgyorsítható a Wilson-teszt, hisz nem kell p-2 darab szorzást elvégezni, de még így is lassúbb, mint a naív módszer.
|
| Előzmény: [3179] Maga Péter, 2010-02-01 08:11:25 |
|
|
|



 -t meg kellene mondani. :)
-t meg kellene mondani. :)

 x
x 0. Határozzuk meg az
0. Határozzuk meg az 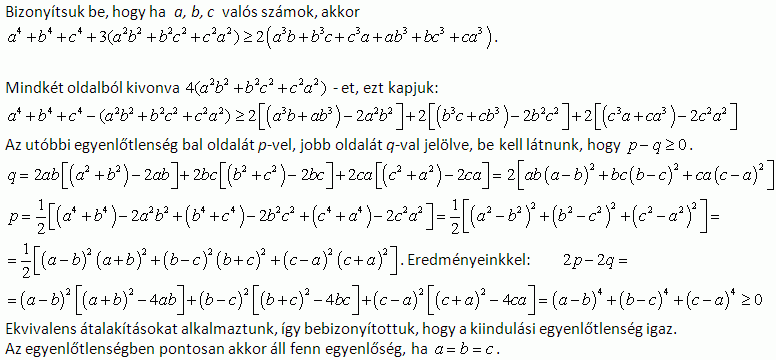


 aij(mod p), ahol j
aij(mod p), ahol j
 1, egyik sem lehetséges, hiszen p prím, tehát a táblázat latin négyzet.
1, egyik sem lehetséges, hiszen p prím, tehát a táblázat latin négyzet. 