| [318] Suhanc | 2004-04-17 22:12:21 |
 Kedves László!
Azt hiszem, van megoldásom a feladatodra... remélem, nem kapkodtam el...
Bárhogyan is választjuk ki a 8 számot /a feladat feltételeinek megfelelően/, mindig azonos lesz a számok összege. Ez az összeg 260.
Jelöljük ugyanis X-szel, ha egy számot kiválasztottunk... Helyezzük el az X-eket, az első oszlopban. Innen az összes kiválasztás elértő, ha a sorokban lévő X-eket /minden sorba 1 van/ 0;1;2;...6;7 mezővel jobbra toltuk, hisz ekkor minden oszlopban pontosan 1 X-lesz. Azaz, minden lehetséges kiválasztásnál az számok összeg kiszámolható úgy, hogy az (1+9+17+25+33+41+49+57)-hez még (0+1+2+3+4+5+6+7)-et adunk. Így tehát a számok összege valóban minden esetben 260 lesz.
|
|
| [317] lorantfy | 2004-04-17 16:46:46 |
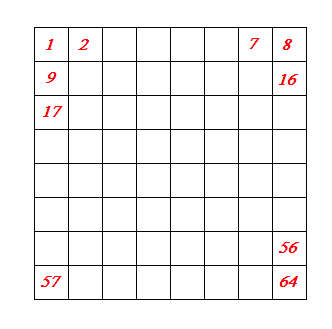
 72. feladat: Számozzuk meg a 8x8-as sakktábbla mezőit balról jobbra, fenntről lefelé.
Kiválasztunk 8 számot úgy, hogy minden sorból és minden oszlopból csak egy számot választhatunk.
Mennyi a 8 szám összegének minimuma és maximuma?
|
 |
|
| [316] Csimby | 2004-04-16 21:46:51 |
 71.feladat Színezzük a sakk tábla mezőit tetszőleges módon két különböző színnel. Bizonyítsuk be, hogy az egyik színre színezett mezők bejárhatók egy királynővel (átlósan, vízszintesen és függőlegesen tud mozogni), úgy, hogy a királynő áthaladhat a másik színre színezett mezők felett, de azokon nem állhat meg! Egy mezőn többször is áthaladhat.
|
|
| [315] lorantfy | 2004-04-15 22:24:35 |
 Kedves NádorP!
A b) rész 2. felében Neked van igazad. Én elkapkodtam. Nem elég a sort és az oszlopot kiválasztani... A bástyás példa szemléletesen mutatja, hogy itt még 72 megoldás van, tehát a páratlan esetben összesen 88.
|
| Előzmény: [313] nadorp, 2004-04-15 14:42:46 |
|
| [314] nadorp | 2004-04-15 14:45:01 |
 Kedves László !
Most láttam, hogy Te is válaszoltál. A páratlan esetben különbözünk, majd én átgondolom a megoldást.
N.P.
|
|
| [313] nadorp | 2004-04-15 14:42:46 |
 Sziasztok !
Egyelőre csak a konkrét esettel foglalkoztam, a szimmetrikus,elforgatott megoldásokat különbözőnek tekintettem.
a) Legyen minden sorban és oszlopban páros sok korong. Ez csak úgy lehet, ha 2 sorban 4 korong és 1 sorban 2 van vagy 1 sorban 4 korong és háromban kettő. Az első eset nem fordulhat elő, mert ekkor két oszlopban is három korong lenne.Ezért marad a második lehetőség, de ekkor ugyanígy egy oszlopban 4 korong és 3 oszlopban 2 korong van. Válasszunk ki egy sort és egy oszlopot, ahol 4 korong lesz. Ezt megtehetjük 16-féleképpen.Tekintsünk egy, a kiválasztott sortól különböző sort. Ide 3 helyre tehetünk korongot.Ezek után még egy, az előzőektől különböző sort tekintve már csak két lehetőség közül választhatunk.Így az összes esetek száma 16.3.2=96.
b)Legyen minden sorban és oszlopban páratlan sok korong. Ez csak úgy lehet, ha 3 sorban és oszlopban 3 korong van, és egy sorban és egy oszlopban egy korong van.Válasszunk ki egy sort és egy oszlopot, ahol 1 korong lesz. Két eset lehetséges. Ha a kiválasztott sorban és oszlopban összesen csak 1 korong van, akkor a maradék összes, nem kizárt 9 mezőre kerül korong. Ez összesen 16 eset.Ha a kiválasztott sorban és oszlopban összesen 2 korong van, akkor könnyen látható,hogy a két korong által meghatározott sorok és oszlopok másik két kereszteződésében nem lehet korong.Így 8 mezőre kell 8 korongot elhelyezni, azaz a kiválasztott 2 korong egyértelműen meghatározza a többi helyzetét. Az esetek száma annyi, ahányféleképpen el lehet helyezni két bástyát egy 4x4 sakktáblán úgy, hogy ne üssék egymást.Egy bástyához 9-féleképpen lehet másikat feltenni, ez összesen 9.16=144 eset, de mindegyiket kétszer számoltuk. Azt kaptuk tehát, hogy páratlan esetek száma 16+72=88.
Remélem nem bonyolítottam ( és nem számoltam) el.
N.P.
|
| Előzmény: [310] lorantfy, 2004-04-15 12:54:58 |
|
| [312] lorantfy | 2004-04-15 14:41:17 |
 Kedves Károly!
Ügyes ki példa ez, csak kevés az időm.
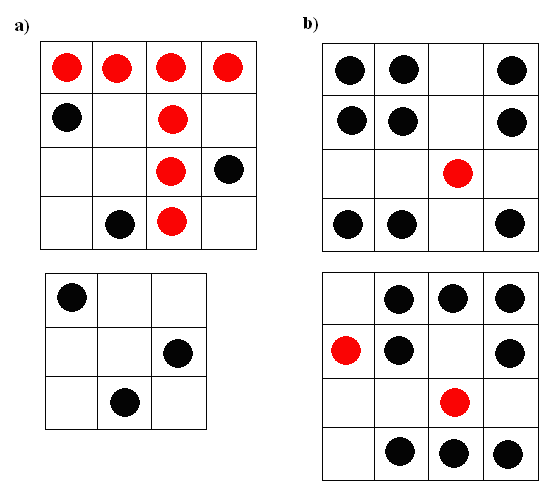
Megoldások száma a 70. feladatnál:
a) esetben 10=4+2+2+2. Nézzük először a 4-es sorok és oszlopok helyzetét. Bármelyik sor bármelyik oszloppal párosítható. Ez 16 lehetőséget jelent, de minden elrendezésnél még 3 korong helyét variálhatjuk. A megmaradó 3x3-as négyzetrácsban kell elhelyeznünk a 3 korongot, úgy, hogy minden sorban és oszlopban csak 1 lehet. Ez 6 féleképpen lehetséges. Így a megoldások száma 6x16=96.
b) esetben, csak a 10=3+3+3+1 felbontás lehetséges, így azokat a megoldásokat könnyen összeszámolhatjuk, ahol a sorban és oszlopban egyedülálló ugyanaz a korong, ami bármelyik mezőben állhat, ez 16 megoldást jelent.
De sajnos vannak olyan esetek is mikor a sorban egyedülálló koron egy oszlopban álló 3-as része és az oszlopban egyedül alló egy sorban álló 3-as része. Ezek az egyedülálló korongok bármelyik sor és oszlop párban állhatnak, ha jól gondolom akkor ez is 16 eset. Összesen 32 megoldás.
Azért jó lenne, ha utánnagondolnátok, mert ez nagyon kapkodva született! Vannak asszimmetrikus megoldások.
|
 |
| Előzmény: [311] Hajba Károly, 2004-04-15 13:05:26 |
|
|
| [310] lorantfy | 2004-04-15 12:54:58 |
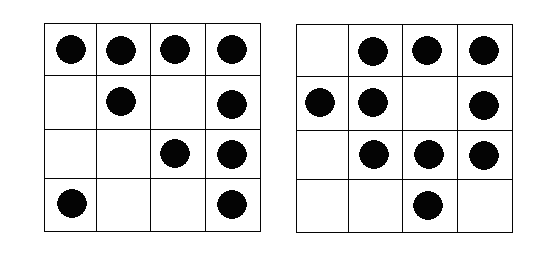
 70. feladat megoldása: Egyenlőre csak beraktam a korongokat a négyzetrácsba. Most még ki kéne találni hány megoldás van! Aztán általánosítani nxn-es rácsra és k<n2 korongra. Mikor oldható meg egyáltalán?
|
 |
| Előzmény: [309] Hajba Károly, 2004-04-15 07:47:30 |
|
| [309] Hajba Károly | 2004-04-15 07:47:30 |
 70. feladat
Adott egy fehér 4*4-es négyzetrács és 10 db fekete korong. Helyezzük el a korongokat egy-egy négyzetre az alábbi feltételek szerint:
a) minden sorban és oszlopban páros korong legyen.
b) minden sorban és oszlopban páratlan korong legyen.
HK
|
|
| [308] Hajba Károly | 2004-04-14 01:37:05 |
 Kedves Sirpi és Csimby!
Köszi a pontosítást, s mivel tetszett a feladat, elmélázatam az általánosításán is. Íme az általános megoldóképlet a maximumértékre, ahol N pozitív egész:
![f(N)=3^{\Big[\frac{N-2}{3}\Big]}*\Big(2+3*\Big\{\frac{N-2}{3}\Big\}\Big)](keplet.cgi?k=2B0BB2181C2EA873)
HK
|
| Előzmény: [307] Sirpi, 2004-04-12 15:16:43 |
|
| [307] Sirpi | 2004-04-12 15:16:43 |
 Valóban a 3668 a maximum, nézzük is, miért.
Tegyük fel, hogy felosztottuk a 2004-et néhány pozitív egész szorzatára.
Ha van a számok közt 1-es, akkor egy másik k számmal összevonva 1.k<1+k miatt növeljük a szorzatot.
Ha van olyan k szám köztük, ami legalább 4, akkor nem rontunk, ha k-t kicseréljük 2.(k-2)-re, sőt, k 4 esetén jav³tunk is. 4 esetén jav³tunk is.
Így feltehető, hogy csupa 2-es és 3-as tényezőkből áll a szorzat. De mivel 2.2.2<3.3 és 2+2+2=3+3, így legfeljebb 2 db. 2-es lehet az optimális szorzatban. De a 2004 osztható 6-tal, ami miatt a 2-esek száma 3-mal osztható kell legyen. De 0 és 2 közt csak a 0 osztható 3-mal, így az optimális szorzatban 0 db 2-es és 668 db. 3-as kell legyen.
Nem láttam be, de triviális, hogy valóban van maximum...
S
|
| Előzmény: [306] Hajba Károly, 2004-04-12 01:45:34 |
|
| [306] Hajba Károly | 2004-04-12 01:45:34 |
 Megoldás a 69.feladatra:
Kezdjük el a 2004-et az n N>2 számokkal elosztani és utána képezni az N>2 számokkal elosztani és utána képezni az  -t. Az Smax-ot az -t. Az Smax-ot az 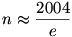 helyen kapjuk, így helyen kapjuk, így  . .
Ültessük most ezt át az egész számokra, azaz a 2004-t osszuk fel 2-es és/vagy 3-as számok összegére. (Várhatóan 738 darabra), majd ezeket összeszorozni. Erre közelítést az alábbi egyenletrendszer megoldásával tehetünk:
2*n+3*m=2004
n+m=738
Innen az S=2210*3528 szám adódik, de érdekes módon nem ez adja a jó megoldást, hanem az S=3668.
HK
Ui: Remélem, jó az elképzelésem, s egyébként kellemes locsolkodást mindenkinek :o)
|
| Előzmény: [305] Csimby, 2004-04-11 21:48:22 |
|
| [305] Csimby | 2004-04-11 21:48:22 |
 69.feladat Számítsuk ki olyan pozitív egész számok szorzatának maximumát, amelyek összege 2004.
|
|
| [304] Sirpi | 2004-04-09 10:05:59 |
 Ezt a feladatot nem ismertem, viszont némi agyalás után rájöttem, hogy a feladat nem más, mint egy többdimenziós Mérgezett csoki játék. Ez alapján az a válasz, hogy ha n 1, akkor az első játékosnak van nyerő stratégiája (viszont ezt a stratégiát nem lehet megadni, általánosan csupán egzisztenciabizonyítás adható). 1, akkor az első játékosnak van nyerő stratégiája (viszont ezt a stratégiát nem lehet megadni, általánosan csupán egzisztenciabizonyítás adható).
Ezután a bevezető után nem is lőnem le (teljesen :-) ) a megoldást, de leírom, hogy mi is az a 2 dimenziós Mérgezett csoki játék:
Van egy n×m méretű csokink, melynek a bal felső kockája mérgezett, valamint egy L alakú késünk, mellyel a csoki rácsai mentén vághatunk. A kést csak úgy forgathatjuk, hogy a levágandó rész jobb alulra essen. A 2 játékos felváltva vág a csokiból, és amit levágnak, azt meg is eszik. Az veszít, akinek a mérgezett kiskocka marad.
Innen már csak azt kell kitalálni, hogy a 2 feladatnak mi köze van egymáshoz, és miért nyer (majdnem) mindig az A játékos...
Remélem, sikerült mindenkit kellően összezavarnom :-)
Könnyű pótfeladat:
a) adjuk meg a nyerő stratégiát, ha a csoki 2×n-es
b) ha n×n-es
Sirpi
|
| Előzmény: [303] Csimby, 2004-04-04 23:25:47 |
|
| [303] Csimby | 2004-04-04 23:25:47 |
 Talán van aki nemismeri:
68. feladat A és B a következő játékot játszák: Kiindulnak egy adott N számból és felváltva mondják N-nek egy-egy osztóját, úgy hogy senki sem mondhat olyan osztót ami az eddig elhangzott osztók egyikének osztója. Az a játékos veszít aki már csak N-et tudja mondani. Mikor, kinek van nyerő stratégiája?
|
|
|
|
|
| [299] Csimby | 2004-03-26 22:12:12 |
 Én is ezt a megoldást ismerem, amit Nadorp és Onogur összehozott, de a másik is érdekes. Szerintem is nagyon szép.
Kicsit feleslegesnek tartottam ennyi miatt hozzászólást írni ezért arra gondoltam megnézem a What's Special About This Number? lapot, mit ír a 300-ról (mivel ez a 300. hozzászólás, ha valaki meg nem előz) és ezt találtam: "300 is the largest possible score in bowling", fantasztikus. Egyébként vannak "tényleg" érdekes(ebb) dolgok is ezen a honlapon.
|
|
|
| [297] Sirpi | 2004-03-26 08:57:09 |
 Na, akkor egy próba:
Tudjuk, hogy 0<a<b<c, és használjuk Onogur szemfüles átalakítását:
f(x)=(a-x)(b-x)c+a(b-x)(c-x)+(a-x)b(c-x)
Ekkor
f(a)=a(b-a)(c-a)>0
f(b)=(a-b)b(c-b)<0
f(c)=(a-c)(b-c)c>0
Az előjelváltások és f folytonossága miatt muszáj lenni gyöknek mind az (a,b), mind a (b,c) intervallumban.
S
|
| Előzmény: [294] Hajba Károly, 2004-03-26 00:57:49 |
|
| [296] nadorp | 2004-03-26 08:54:52 |
 Sziasztok !
Adok egy megoldást a 67. feladatra. A bizonyítás nem elemi, de a feladat alapötlete szerintem innen származik.
Tekintsük a p(x)=abcx3-(ab+ac+bc)x2+(a+b+c)x-1 polinomot. Könnyen látható,hogy 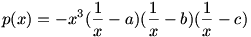 miatt a p(x) gyökei az miatt a p(x) gyökei az 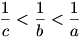 számok. A polinomnak három valós gyöke van, ezért létezik egy lokális maximuma és egy lokális minimuma. Ezeket a szélsőértékeket a polinom az számok. A polinomnak három valós gyöke van, ezért létezik egy lokális maximuma és egy lokális minimuma. Ezeket a szélsőértékeket a polinom az 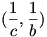 illetve a illetve a 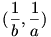 intervallumokon veszi fel. A szélsőértékek helyeit a p'(x)=0 egyenlet gyökei adják.Viszont a intervallumokon veszi fel. A szélsőértékek helyeit a p'(x)=0 egyenlet gyökei adják.Viszont a
p'(x)=3abcx2-2(ab+ac+bc)x+(a+b+c)=0 egyenlet gyökei nyilván a
(a+b+c)x2-2(ab+ac+bc)x+3abc=0 egyenlet gyökeinek a reciprokai, ezért ennek az egyenletnek a gyökei az (a,b) illetve (b,c) intervallumokba esnek.
|
|
|
| [294] Hajba Károly | 2004-03-26 00:57:49 |
 Kedves Csimby!
A 65. feladatnál az alábbi részeredményre jutottam:
A (a+b+c)x2-2(ab+bc+ac)x+3abc=0 egyenletet átrendezve az következő egyenletet kapjuk:
(a-x)(b-x)c+a(b-x)(c-x)+(a-x)b(c-x)=0
a) Ha x<a akkor az összeg mindhárom tagja pozitív lesz, míg ha x>c akkor mindhárom negatív lesz, s ez ellentmondás. Tehát a<x<c.
b) Ha rendre x= a, b, c, akkor az összeg két-két tagja rendre zérus, míg a harmadik nem. Így ez is ellentmondás. Tehát x (a,b,c) (a,b,c)
c) Ha a<x<b vagy b<x<c, akkor az összeg 3. tagja mindig negatív, a másik két tag előjele ellentétes, így mindkét tartományban lehetséges gyök; de eddig még nem leltem meg a megoldást, mellyel bizonyíthatnám, hogy két külön tartományba is kell kerülniük. :o(
HK
|
| Előzmény: [289] Csimby, 2004-03-24 00:40:29 |
|











 4 esetén jav³tunk is.
4 esetén jav³tunk is.  N>2 számokkal elosztani és utána képezni az
N>2 számokkal elosztani és utána képezni az 