| [3483] Sirpi | 2011-10-03 10:36:54 |
 Végiggondoltam ezt az utat is, és tényleg igaz az az állítás, hogy: Ha egy 3x7-es téglalapban elhelyezünk 11 korongot, akkor a korongok közül van 4, amik egy (álló) téglalap 4 csúcsát alkotják.
Amit leírtál, az csak az a rész, amikor az egyik oszlopban 7 korong van, ilyenkor tényleg 9 a maximum. Viszont mi a helyzet, ha a legtöbb korongot tartalmazó oszlopban 6,5,4 korong szerepel? Végig lehet nézni, ilyenkor is kijön, hogy 10 után elakadunk.
Szóval ez az út is járható, de személy szerint macerásabbnak érzem, mint a (3 hosszú) sorok szerinti esetvizsgálatot.
|
| Előzmény: [3481] phoenix, 2011-10-03 01:35:47 |
|
| [3482] Sirpi | 2011-10-03 09:03:01 |
 Ez a feladat konkrétan a Fazekasban volt nálam felvételi feladat, 92-ben, azóta kedvencem.
A bizonyításhoz nem azt érdemes nézni, hogy az egyik színből legalább 11 van, hanem azt, hogy a sorok összesen 8-félék lehetnek. Ha van két azonos sor, készen vagyunk. Ha van egyszínű sor, szintén. Ezeket érdemes végiggondolni, és meg is van a bizonyítás (és az is látszik, hogy 3x6-ra hogy néz ki az ellenpélda).
|
| Előzmény: [3481] phoenix, 2011-10-03 01:35:47 |
|
| [3481] phoenix | 2011-10-03 01:35:47 |
 Gondoltam ilyenre Azért nem lehetséges?, mert 21 négyzet van, és mondjuk optimális esetben 10-10-et tudunk elhelyezni egyik-egyik színből, ha az egyikből több van, akkor szinte garantált hogy négy négyzet összejön ami meghatároz egy téglalapot, elhelyezünk egymás alá 7-et azután legalsóba vízszintesen ez eddig 9 és bárhova tesszük tizediket akkor már meglesz, nem beszélve a másik színről hogy abból jóval több van
|
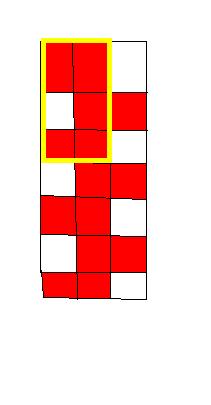 |
| Előzmény: [3480] Róbert Gida, 2011-10-03 01:10:57 |
|
| [3480] Róbert Gida | 2011-10-03 01:10:57 |
 "igazából bármilyen téglalapot színezel is ki, mindig lesz négy olyan négyzet, ami egy téglalapot határoz meg... "
helyesen megkérdezve: igazából bármilyen téglalapot színezel is ki, mindig lesz négy olyan pont, ami egy egyszínű téglalapot határoz meg...
Ez pedig nem igaz.
A feladatot skatulyaelvvel lehet megoldani. Ramsey tipusú problémának is tekintheted. A feladat több színnel és magasabb dimenzióban is érdekes. Tudtommal 2d-ben és 4 színnel is már megoldatlan, hogy mely téglalapokat lehet kiszínezni, hogy ne legyen benne monokromatikus téglalap. Véges sok, de még mindig marha sok színezést kéne végignézni ehhez.
|
| Előzmény: [3479] phoenix, 2011-10-02 18:38:08 |
|
|
|
| [3477] phoenix | 2011-10-02 14:20:22 |
 321. Ha a síkot (tekintsük négyzetrácsosnak) kiszínezzük két fajta színnel, legyen barna és kék, bárhogy is választjuk meg a színeket, mindig lesz négy azonos színű, amelyek egy téglalap csúcsait határozzák meg. A kérdés hogy miért?
|
|
| [3476] Róbert Gida | 2011-09-20 15:16:04 |
 Olyan Tom és Jerry tipusú feladat. 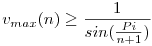 igaz, ez pont a szabályos (n+1) szögben egy oldal hosszának a reciproka. Ezen pontokban jelenjenek meg a morzsák (egy csúcsban legfeljebb egy). Ha a fenti egyenlőtlenség nem teljesül, akkor 1 morzsa gyorsabban jelenik meg, mint ahogyan azt meg tudná enni a hangya (hiszen a szabályos sokszögben csúcsok közti legrövidebb távolság az oldal hossza). Így ekkor véges időn belül olyan helyzet lesz, hogy a hangya egy csúcsban van (éppen megette a morzsát), és a többi n csúcsban morzsa van. 1 percen belül morzsát teszünk le, de ne abba a csúcsba ahol a hangya éppen volt. Így egy morzsát sem tud elérni, és n+1 morzsa lesz a csúcsokban. (egyikben most kivételesen kettő). igaz, ez pont a szabályos (n+1) szögben egy oldal hosszának a reciproka. Ezen pontokban jelenjenek meg a morzsák (egy csúcsban legfeljebb egy). Ha a fenti egyenlőtlenség nem teljesül, akkor 1 morzsa gyorsabban jelenik meg, mint ahogyan azt meg tudná enni a hangya (hiszen a szabályos sokszögben csúcsok közti legrövidebb távolság az oldal hossza). Így ekkor véges időn belül olyan helyzet lesz, hogy a hangya egy csúcsban van (éppen megette a morzsát), és a többi n csúcsban morzsa van. 1 percen belül morzsát teszünk le, de ne abba a csúcsba ahol a hangya éppen volt. Így egy morzsát sem tud elérni, és n+1 morzsa lesz a csúcsokban. (egyikben most kivételesen kettő).
n=1-re még pontos is a formula.
|
| Előzmény: [3475] Sirpi, 2011-09-20 13:30:35 |
|
| [3475] Sirpi | 2011-09-20 13:30:35 |
 Sziasztok!
Tegnap jött egy ötlet, nem lett még belőle egzakt feladat. Azért leírom, hátha másnak is megindítja a fantáziáját.
Szóval induljunk ki egy 1 egység átmérőjű körből. Ebben van egy pontszerű hangya, és percenként véletlenszerűen (vagy direkt szívatós helyen) megjelenik egy-egy morzsa.
Ha a hangya sebessége legalább 1 egység/perc, akkor minden morzsát össze tud szedni, mielőtt a következő megjelenne.
Viszont mi van, ha a hangya lassabb? Tehát mennyire lehet kicsi a maximális sebessége, hogy egyszerre legfeljebb 2, 3 stb. morzsát engedhet meg a körön (minden darabszámra lehetne mondani egy korlátot).
Nem tudom, hogy van-e egyáltalán értelme az egésznek, sokat még nem gondolkodtam rajta, de hátha kijön belőle valami érdekes.
Megjegyzés: az ötletet a Plants vs. Zombies játék adta, amiben van egy Zen garden nevű rész, ahol a virágok pénzeket potyogtatnak, és egy csiga próbálja őket összeszedni (és a csiga csokival gyorsítható). Ha a csiga lassú, a pénzek elszaporodnak... Ezen kezdtem agyalni, hogy mennyire számít a csiga sebessége, és próbáltam "lecsupaszítani" a problémát.
|
|
|
|
| [3472] Kemény Legény | 2011-09-03 07:09:53 |
 Tibixe példája tökéletes ellenpélda, megcáfolja az állítást, azaz "létezik olyan periodikus függvény, amely mindenhol értelmezett, értékkészlete R".
Ha esetleg a folytonosságot is ki akarod kötni, akkor "olyan periodikus folytonos függvény nem létezik, amely mindenhol értelmezett, értékkészlete pedig R". Indirekten ugyanis ha lenne ilyen p periódusú f függvény, akkor annak az értékkészlete ugyanaz lenne, mint a [0,p] intervallumon (kompakt halmazon) felvett értékkészlete, ami folytonos függvény esetén szintén kompakt (korlátos és zárt), ezért nem lehet az a teljes R.
|
| Előzmény: [3470] Paralelepipedon, 2011-09-02 20:22:35 |
|
| [3471] Tibixe | 2011-09-02 23:02:02 |
 Erre többek között lentebbi f függvény cáfolat, mert értelmezési tartománya és értékkészlete egyaránt a valós számok halmaza, továbbá 2 -periodikus és mindenhol értelmezett. -periodikus és mindenhol értelmezett.
A kérdésednek akkor van matematikai tartalma, ha megköveteled, hogy a függvény folytonos legyen.
|
| Előzmény: [3470] Paralelepipedon, 2011-09-02 20:22:35 |
|
| [3470] Paralelepipedon | 2011-09-02 20:22:35 |
 A feladatot elég félreérthetően fogalmaztam meg sajnos. A lényege az lenne, hogy azt bizonyítsuk vagy cáfoljuk, hogy minden valós, periodikus függvény esetén, ahol az értelmezési tartomány és az értékkészlet nem korlátos sem alulról, sem felülről van olyan valós szám, amely nem eleme az értelmezési tartománynak.
|
|
|
|
| [3467] Paralelepipedon | 2011-09-02 17:55:54 |
 Nemrég eszembe jutott az alábbi feladat. Sajnos még bizonyítani és cáfolni sem tudom.
531. Adott egy valós, periodikus függvény, melynek értelmezési tartománya és értékkészlete nem korlátos alulról és felülről sem. Bizonyítsuk (vagy cáfoljuk), hogy van olyan szám, mely nem eleme az értelmezési tartománynak.
|
|
|
|
| [3464] Tóbi | 2011-08-19 12:07:41 |
 530. Tegyük fel, hogy lehetőséget kaptunk arra hogy a következő játékot játsszuk. Mutatnak nekünk két egyforma lezárt borítékot egy asztalon. Elárulják, hogy az egyikben kétszer annyi pénz van, mint a másikban. Ezután arra kérnek, hogy vegyük kézbe az egyik általunk választott borítékot. A játékvezető döntés elé állít minket: Azt a borítékot kérjük, ami nálunk van, vagy cserélünk és inkább a másikat visszük el? Mielőtt döntenénk hárman is adnak tanácsot.
1. Ne cserélj! Legyen p a nálad lévő, q az asztalon lévő összeg. Egyenlő eséllyel lesz p<q vagy p>q. Ha p>q, akkor p=2q, így 2q-q=q pénzt buksz. Ha p<q, akkor p=q/2, így q-q/2=q/2 pénzt nyersz. Tehát többet bukhatsz a cserével, mint amit nyerhetsz.
2. Cserélni kell! Ha p<q, akkor q=2p, így a cserével 2p-p=p pénzt nyersz. Ha viszont p>q, akkor q=p/2, tehát p-p/2=p/2 pénzt vesztesz. Megéri tehát cserélni, hiszen kétszer annyit nyerhetsz, mint amennyit veszíthetsz.
3. Mindegy, hogy cserélsz-e. Legyen ugyanis n a kisebb a két borítékban lévő pénz közül. Ha p>q, akkor q=n és p=2n, tehát n-et vesztünk egy cserével. Ha p<q, akkor p=n és q=2n, így a hasznunk n lesz a csere esetén. Ugyanannyi a hasznunk illetve kárunk a két esetben, így mindegy, hogy cserélünk-e.
Melyik tanácsot fogadjuk meg?
|
|
| [3463] Csimby | 2011-06-23 10:35:35 |
 Amit írtam úgy értettem, hogy ha felhasználjuk az amúgy önmagában is érdekes 529.-et, akkor már szinte semmi se kell (annyi, hogy xpd-cx gyökei test szerinti mellékosztályt alkotnak, GF(pd)-szerintit, de ez triv.). De persze ha 529.-et is bizonyítani akarjuk akkor annál már biztos egyszerűbb az amit te írsz.
|
| Előzmény: [3462] Maga Péter, 2011-06-23 09:23:18 |
|
| [3462] Maga Péter | 2011-06-23 09:23:18 |
 Hmmm... lehet, hogy megint elnézek valamit, de én ennél is kevesebbet használtam fel a véges testekről. Konkrétan azt, hogy egy rögzített, p karakterisztikájú testben 1) minden d 1-re legfeljebb egy pd elemű résztest van; 2) a multiplikatív csoport minden véges rendű eleme egy véges résztestet generál. Meg még annyit, hogy egy véges (additív) csoport egy valódi részcsoportjában legfeljebb az összes eleme fele lehet. 1-re legfeljebb egy pd elemű résztest van; 2) a multiplikatív csoport minden véges rendű eleme egy véges résztestet generál. Meg még annyit, hogy egy véges (additív) csoport egy valódi részcsoportjában legfeljebb az összes eleme fele lehet.
|
| Előzmény: [3459] Csimby, 2011-06-22 13:43:32 |
|
|
|
| [3459] Csimby | 2011-06-22 13:43:32 |
 Igen az a rész elemi, ami nem jelenti azt hogy könnyű rájönni :). Ha jól értem te már megoldottad mindkét részt, tehát talán nem baj ha segítek a végtelenséghez annak akit érdekel. Lehet máshogy is persze, de talán úgy kell a legkevesebbet tudni hozzá véges testekről ha felhasználjuk ezt:
529. Legyen T test p>0 karakterisztikával, A pedig egy véges additív részcsoportja, pd elemszámmal. Ekkor 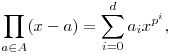 ahol az együtthatók T-ben vannak. ("fundamental theorem of additive polynomials" egyik iránya) ahol az együtthatók T-ben vannak. ("fundamental theorem of additive polynomials" egyik iránya)
|
| Előzmény: [3458] Maga Péter, 2011-06-22 12:41:32 |
|







 /2-ben értelmezett ?
/2-ben értelmezett ?



 1-re legfeljebb egy pd elemű résztest van; 2) a multiplikatív csoport minden véges rendű eleme egy véges résztestet generál. Meg még annyit, hogy egy véges (additív) csoport egy valódi részcsoportjában legfeljebb az összes eleme fele lehet.
1-re legfeljebb egy pd elemű résztest van; 2) a multiplikatív csoport minden véges rendű eleme egy véges résztestet generál. Meg még annyit, hogy egy véges (additív) csoport egy valódi részcsoportjában legfeljebb az összes eleme fele lehet.