| [3546] FlagD | 2012-01-15 13:07:44 |
 Akkor én is lelövöm az én "megoldásom".A két számot a-val, és b-vel fogom jelölni. b=a+k (vagyis a és b között k-1 darab számra kell teljesülnie a feltételnek.)
Az első, ami beugrott, az az ismert feladat, hogy bármely pozitív egész n-re van egymás utáni n darab összetett szám. 6!+1=721 pedig osztható 7-tel, vagyis a=6!, és b=6!+7 jó választás lesz. Azt néztem el, hogy 727 persze nem osztható 7-tel. (No persze annak is be kellett volna ugrani, hogy Wilson-tétele miatt,akkor már pl. 5|4!+1 is igaz, és a=4! is hasonló okok miatt nem megfelelő)
És akkor, hogy lehet jó megoldást adni: Az könnyen látható, hogy a,b>2. Mivel két szomszédos szám legnagyobb közös osztója : (n;n+1)=1, emiatt (a;b-1)>1, és (b;a+1)>1 (és így a-nak, és b-nek kell lennie különböző prímosztójának ). Ha elkezdjük b-1;a-val, illetve b;a+1-gyel az euklideszi-algoritmust, akkor mindkét esetben az első maradék: k-1. Ez a fentiek miatt azt jelenti, hogy k-1-nek legalább két különböző prímosztója van. Nézzük sorba az eseteket (amikor pontosan két prímosztója van k-1-nek!)
1. Ha k-1=2*3. Ekkor b=a+7. (Legyen most 2|a, és 3|b; a fordított eset hasonló!) Ekkor a+1 (=b-6 miatt!); a+2; a+4 (=b-3 is!); a+6 számok "jók", de a+3=b-4 mind a-val, mind b-vel relatív prím. Vagyis ez az eset nem lehet!
2-3. Hasonlóan k-1=2*7 (2|a,7|b) esetre pedig a+7=b-8 "rossz"; míg k-1=2*5 (2|a,5|b) esetre: a+5=b-6 "rossz", amennyiben 3 nem osztója b-nek, és a+9=b-2 "rossz", amennyiben 3 nem osztója a-nak (és persze 3 vagy a-t, vagy b-t oszthatja csak!)
4. Legyen most k-1=3*5 (itt lesz a jó megoldás), illetve 3|a, 5|b! Válasszuk a-t párosnak is (ekkor persze b is az). Így a+1(=b-15 miatt), a+2, a+3,a+4;a+6(=b-10 miatt is);a+8;a+9;a+10;a+11(=b-5 miatt);a+12;a+14;a+15 eleve "jók" (a,és b választása miatt). a+5=b-11; a+7=b-9; a+13=b-3 számokat kell vizsgálnunk csak. Mivel 3 nem osztja b-t, 5 pedig a-t, a fenti három vizsgált szám csak úgy lehet "jó", ha 11|b, míg 7*13|a teljesül. Most ott tartunk, hogy 2*3*7*13=546|a , míg 2*5*11=110|b. Vegyük észre, hogy 5*2*5*11=550 "közel" van 546-hoz. Ha mind 546-t, mind 550-t szorozzuk 4-gyel, akkor megfelelő a-t, b-t kapunk. Vagyis a=2*2*2*3*7*13 = 2184 , és b=2*2*5*5*11 = 2200 valóban jó választás.
Azt még nem látom pontosan, hogy miért ez a legkisebb. Ja és elnézést jonastól (természetesesn Övé az érdem), hogy lelőttem, hogy a megoldása hogy jöhetett ki, a rossz megoldásom miatt próbáltam "kiköszörülni a csorbát"!
Üdv!
|
| Előzmény: [3545] jonas, 2012-01-15 11:16:07 |
|
|
| [3544] jonas | 2012-01-15 11:09:56 |
 Esetleg úgy érted, olyat találtál, ahol a két szám különbsége van 700 és 800 között? Mert olyan megoldás biztosan nincsen, ahol mindkét szám 800 alatt van.
|
| Előzmény: [3543] FlagD, 2012-01-15 10:14:46 |
|
| [3543] FlagD | 2012-01-15 10:14:46 |
 Nekem megvan, de nem lőném le teljesen, csak annyira, hogy van ilyen számpár.
Egy ismert számelmélet feladat jutott rögtön eszembe, és 700, és 800 között találtam jó megoldást (nem tudom ez a számpár-e a legelső).
|
| Előzmény: [3541] Sirpi, 2012-01-15 07:40:05 |
|
|
| [3541] Sirpi | 2012-01-15 07:40:05 |
 Tegnap este találtam ki ezt a feladatot, és szerintem érdekes:
Van-e két olyan nem szomszédos pozitív egész, hogy a köztük lévő minden számra teljesül, hogy nem relatív prím a két szám valamelyikéhez? (pl. a 90, 98 pár jó lenne, ha a 97 nem lenne köztük.) Egyébként sikerült is megoldani.
|
|
|
| [3539] Róbert Gida | 2012-01-12 00:47:15 |
 Első feladatra: ha a háromszög tompaszögű, akkor trivi, mert a szorzat akkor negatív. Egyébként számtani-mértani egyenlőtlenség, majd Jensen egyenlőtlenség a [0,Pi]-n konkáv cos fv-re
Második feladatra nincs tippem.
Utolsó feladat: cos-ra használhatod a cos tételt, 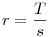 és és 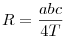 , ahol T a terület, s a félkerület. Továbbá T-re a Héron képletet. Ekkor mindenhol már csak a,b,c szerepel, azaz egy azonosságot kell kapnod, ha mindent behelyettesítesz. (itt már nem is lényeges, hogy ezek egy háromszög oldalai is.) , ahol T a terület, s a félkerület. Továbbá T-re a Héron képletet. Ekkor mindenhol már csak a,b,c szerepel, azaz egy azonosságot kell kapnod, ha mindent behelyettesítesz. (itt már nem is lényeges, hogy ezek egy háromszög oldalai is.)
|
| Előzmény: [3537] onkiejoe, 2012-01-11 23:45:20 |
|
|
| [3537] onkiejoe | 2012-01-11 23:45:20 |
 Sziasztok! Lenne néhány feladatom, amin jó pár napja ülök, de egyszerűen nem tudom lebirkózni őket. Már mindent megpróbáltam, amit tudtam, de nem tudok rájönni a megoldás kulcsára. Két szélsőérték-feladat (igazolni kell minden háromszögre, melynek szögei A, B és C, valamint megmondani, hogy milyen A, B, C esetén van egyenlőség):
cos(A)*cos(B)*cos(C) 1/8 1/8
(itt a * sima szorzásjel akar lenni)
cos(A)+cos(B)+cos(C) 3/2 3/2
A feladat "trükkje" az lenne, hogy nem szabad deriválást alkalmazni. Egyébként innen származnak: (12. és 9. feladat) És van még egy, ez már nem szélsőérték (szintén bizonyítandó, az előzőektől függetlenül):
cos(A)+cos(B)+cos(C)=(r+R)/R
(r: beírható kör sugara, R: körülírt kör sugara)
Minden segítséget, választ, és esetlegesen megoldást is előre köszönök!
(És elnézést kérek, hogy nem igazán ismerem ki magam a program kód- és jelrendszerén.)
O.
|
|
|
|
|
| [3533] jonas | 2011-12-18 18:40:56 |
 Az n pozitív egész számot szeretnénk előállítani. Ehhez keressünk egy p prímet, ahol n<p. Ekkor bármilyen k természetes számra n=(pk+n)-pk. Mármost (pk+n) relatív prím pk-tól, mert az utóbbinak az egyetlen prímosztója a p, az előbbi pedig nem osztható p-vel.
|
| Előzmény: [3529] Sirpi, 2011-12-18 10:51:32 |
|
|
|
| [3530] Róbert Gida | 2011-12-18 11:57:45 |
 Legyen B=4*n2+4*n+1=(2*n+1)2 és A=4*n2+5*n+1=(n+1)*(4*n+1). Ekkor A-B=n, itt A,B összetett a faktorizáció miatt. És relatív prímek, hiszen:
lnko(A,B)=lnko(A-B,B)=lnko(n,4n2+5n+1)=lnko(n,1)=1
|
| Előzmény: [3529] Sirpi, 2011-12-18 10:51:32 |
|
| [3529] Sirpi | 2011-12-18 10:51:32 |
 A feladatom nem teljesen explicit, de sebaj.
Adjunk minél egyszerűbb konstruktív bizonyítást arra, hogy minden pozitív egész szám előáll két relatív prím összetett szám különbségeként.
|
|
|
| [3527] Fálesz Mihály | 2011-12-07 11:05:19 |
 L'Hospital szabállyal:
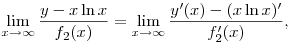
ha 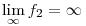 és a jobboldali határérték létezik. és a jobboldali határérték létezik.
Azt már tudjuk, hogy ln y=ln x+ln ln x+o(1).
y'(x)-(x.ln x)'=ln y-ln x-1=ln ln x+O(1).
Olyan f2 kell tehát, aminek a deriváltja kb. ln ln x. Az x.ln ln x ilyen, mert a ln ln x lassan nő, de parciális integrálással is megtalálhatnánk:
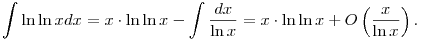
|
| Előzmény: [3526] Lóczi Lajos, 2011-12-07 10:14:29 |
|
|
|
| [3524] Lóczi Lajos | 2011-12-07 04:27:31 |
 Egyelőre én is pont eddig jutottam. Igen, jonas, a bizonyítás talán 1 oldalban összefoglalható lenne, tehát teljesen elemi megfontolásokat használtam csak (az Li függvényről is).
Ha f1(x):=xln (x), akkor tehát eddig azt tudjuk, hogy 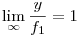 . Az is egyszerűen adódik, hogy . Az is egyszerűen adódik, hogy 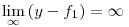 . .
A továbblépéshez keresendő tehát egy f2, hogy  egy véges, nemnulla valós szám legyen. Aztán általában fk, hogy egy véges, nemnulla valós szám legyen. Aztán általában fk, hogy 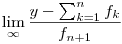 létezik, véges és nemnulla. létezik, véges és nemnulla.
|
| Előzmény: [3521] nadorp, 2011-12-06 15:36:04 |
|
|
|






 R és a harmadik feladatból triviálisan következik a második egyenlőtlenség.
R és a harmadik feladatból triviálisan következik a második egyenlőtlenség.

