| [3771] Micimackó | 2013-08-07 13:22:20 |
 Megsúlyozzuk a mezőket, hogy egy érme mindig egyet érjen. Így 4 mező van, amiből 2-t akarunk üresen és két érmét akarunk a Fálesz verzióban, így ez nem lehet. A b) résznél még a szélső sorra és oszlopra is figyelni kell, mert ott is marad kis plusz üres terület és így nem lesz elég hely.
|
| Előzmény: [3768] w, 2013-08-02 22:28:38 |
|
| [3770] w | 2013-08-03 14:03:32 |
 Egyetértek, csak az eredeti feladatot akartam kitűzni. Lehetne bőven variálni a dolgokat: keressünk kezdő- és célhelyzeteket az (x,y) (x+n,y), (x,y+n) operációra (előbbiből leveszünk, utóbbiakra rárakunk egy-egy zsetont) stb. (x+n,y), (x,y+n) operációra (előbbiből leveszünk, utóbbiakra rárakunk egy-egy zsetont) stb.
Megkérdezném (a feladatot még nem gondoltam át): az (x,y) (x+1,y+1), (x-2,y-1) hasonló változatban legalább hány zsetont kell {(x,y): x,y egész} halmazra rakni, hogy sehogy se lehessen elérni, hogy mondjuk az (1,1)(1,10)(10,10)(10,1) négyzetben ne legyen zseton. (x+1,y+1), (x-2,y-1) hasonló változatban legalább hány zsetont kell {(x,y): x,y egész} halmazra rakni, hogy sehogy se lehessen elérni, hogy mondjuk az (1,1)(1,10)(10,10)(10,1) négyzetben ne legyen zseton.
|
| Előzmény: [3769] Fálesz Mihály, 2013-08-03 05:45:44 |
|
| [3769] Fálesz Mihály | 2013-08-03 05:45:44 |
 Nem értem, hogy az (a) rész miért ennyire bonyolult. Szerintem elég lenne három pont: (0,0), (1,0) és (0,1). Ha kezdetben csak ezeken van zseton, akkor akárhány lépés után is lesz legalább az egyiken.
|
| Előzmény: [3757] w, 2013-07-27 22:52:42 |
|
|
| [3767] Micimackó | 2013-08-02 21:06:06 |
 Nekem úgy tűnik nem lehet, mert nem férnek el. Az első bőven nem fér el (nem is marad elég hely a táblán), a másodikhoz már lenne elég hely, de nincs jól elosztva. Úgyhogy szerintem nem lehet.
|
| Előzmény: [3757] w, 2013-07-27 22:52:42 |
|
|
| [3765] Lóczi Lajos | 2013-08-01 11:04:27 |
 A célkifejezés négyzete azonosan egyenlő a nullára rendezett feltételi egyenletek egy másodfokú polinomjával. A konstans tag 1728-nak adódik, innen egy gyökvonás.
|
| Előzmény: [3762] w, 2013-07-31 12:57:17 |
|
|
|
|
|
|
|
| [3758] w | 2013-07-29 14:59:01 |
 Más. Legyen x,y,z>0. Tudjuk, hogy 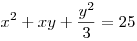 , , 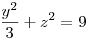 , z2+zx+x2=16. , z2+zx+x2=16.
Számítsuk ki xy+2yz+3zx értékét.
|
|
| [3757] w | 2013-07-27 22:52:42 |
 Egy további érdekes, hasznos, de nem annyira közismert feladat a Városok Viadaláról (1981):
Az első síknegyed rácspontjaira rakunk zsetonokat. Kezdetben (a) az origóban, az (1,0) és (0,1) és (1,1) és (0,2) és (2,0) pontokban van egy-egy zseton, (b) csak az origóban van zseton.
Egy lépésben az (x,y) rácspontból elveszünk egy zsetont - ha az (x+1,y) és (x,y+1) pontokban nincsen - majd utána az (x+1,y) és (x,y+1) pontokra rakunk egyet-egyet.
Elérhetjük-e az (a), illetve (b) esetben, hogy az (a) esetben megnevezett mezők egyikében sem szerepeljen zseton?
|
|
|
| [3755] w | 2013-07-27 21:47:12 |
 Állítás. Létezik c és d konstans a következő tulajdonsággal: tetszőleges a, b pozitív egész számpárhoz létezik pozitív egészekből álló m1,m2,...,mk számsorozat, melyre k<c.ln a+d és
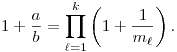
Ha igaz, próbáljunk minél kisebb c és d konstansokat keresni, ha hamis, akkor adjunk ellenpéldá(ka)t.
|
|
| [3754] Róbert Gida | 2013-07-27 21:46:59 |
 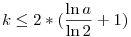 -re teljesül az állítás! Könnyen látható, hogy: -re teljesül az állítás! Könnyen látható, hogy: 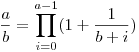 , itt a nevezők egymásutáni egészek; ezt fogjuk használni, hogy rövidebb szorzatot találjunk: vegyü észre, hogy , itt a nevezők egymásutáni egészek; ezt fogjuk használni, hogy rövidebb szorzatot találjunk: vegyü észre, hogy 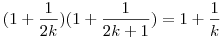 . Ezt az azonosságot alkalmazzuk az (első szinten), ekkor legfeljebb 2 tag marad ki a szorzatból (az első és az utolsó), míg az új . Ezt az azonosságot alkalmazzuk az (első szinten), ekkor legfeljebb 2 tag marad ki a szorzatból (az első és az utolsó), míg az új 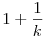 tagokban k egészek itt is egymásutáni egészek lesznek. Így ezt az azonosságot iterative tudjuk újra alkalmazni. Ha 2t-1 tagokban k egészek itt is egymásutáni egészek lesznek. Így ezt az azonosságot iterative tudjuk újra alkalmazni. Ha 2t-1 a<2t akkor t szint van és minden szinten megmarad legfeljebb 2 tag, azaz összesen legfeljebb 2t tag, de (t-1)ln 2 a<2t akkor t szint van és minden szinten megmarad legfeljebb 2 tag, azaz összesen legfeljebb 2t tag, de (t-1)ln 2 ln a, innen triviálisan kapjuk a bizonyítandót. ln a, innen triviálisan kapjuk a bizonyítandót.
|
| Előzmény: [3748] w, 2013-07-27 14:47:25 |
|
|
| [3752] w | 2013-07-27 20:19:56 |
 Jó, bocs, ez most kicsit sötét volt :-)
Kérlek akkor nézz utána a>1 esetének, vagy módosítsd a feladatot úgy hogy értelmes legyen. Felkérlek arra, hogy tégy hozzá valami építő jellegűet is.
|
| Előzmény: [3751] Róbert Gida, 2013-07-27 20:04:10 |
|
|
|
|
| [3748] w | 2013-07-27 14:47:25 |
 Állítás: Létezik c konstans a következő tulajdonsággal: tetszőleges a, b pozitív egész számpárhoz létezik pozitív egészekből álló m1, m2, ..., mk számsorozat, melyre k<c.ln a és
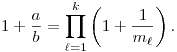
Igazoljuk vagy cáfoljuk.
|
|
| [3747] w | 2013-07-02 07:25:35 |
 Én leginkább erre gondoltam (5. feladat). Lineáris algebrából kb. semmit sem tudok, de úgy látszik, hogy a te megoldásodat írták át elemire. Van viszont lin. algebrakönyvem, előbb-utóbb belenézek. Elnézést a késő válaszért.
Üdv.: w
|
| Előzmény: [3746] jonas, 2013-06-21 21:08:33 |
|




 (x+n,y), (x,y+n) operációra (előbbiből leveszünk, utóbbiakra rárakunk egy-egy zsetont) stb.
(x+n,y), (x,y+n) operációra (előbbiből leveszünk, utóbbiakra rárakunk egy-egy zsetont) stb. 
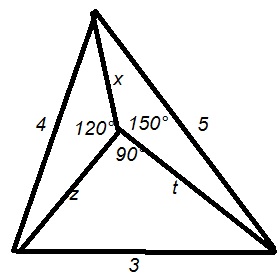

 y2/3+z2=t2+z2=32 Pitagorasz-tétel. A többi már egyértelmű.
y2/3+z2=t2+z2=32 Pitagorasz-tétel. A többi már egyértelmű.


 a<2t akkor t szint van és minden szinten megmarad legfeljebb 2 tag, azaz összesen legfeljebb 2t tag, de (t-1)ln 2
a<2t akkor t szint van és minden szinten megmarad legfeljebb 2 tag, azaz összesen legfeljebb 2t tag, de (t-1)ln 2