| [776] jenei.attila | 2005-02-07 12:07:01 |
 Szia Atosz!
A gyógyszeres feladattal hogy állunk? A rekurzió megoldása elég reménytelennek tűnik. Lehetséges egyáltalán szép zárt alakot adni rá? Vagy esetleg valami ügyes trükkel (ld. őrült légi utasok) egyszerűbben megoldható? Egyébként honnan származik a feladat?
|
|
| [775] Kemény Legény | 2005-02-07 10:44:47 |
 Végtelen sok véletlenszerüen választott 0..1 közti szám között 1 val.szinüséggel lesz végtelen sok a 0..1/2 intervallumban,ekkor pedig a szorzat csak 0-hoz tarthat.Igy 1 a val.szine annak hogy 0 lesz a szorzat.
|
| Előzmény: [774] Atosz, 2005-02-07 09:01:53 |
|
| [774] Atosz | 2005-02-07 09:01:53 |
 Teljesen igazad van, becsapott az an sorozat, ami minden 0 és 1 közötti a esetén 0-hoz tart. Így viszont, jogosnak tűnik Kemény Legény felvetése, miszerint ha véletlenszerűen választunk számokat a (0,1) intervallumból, akkor milyen valséggel lesz a szorzat 0-tól különböző.
|
| Előzmény: [773] Sirpi, 2005-02-07 01:19:36 |
|
| [773] Sirpi | 2005-02-07 01:19:36 |
 Azt viszont furcsálnám, ha 1-nél kisebb számok szorzata nem tartana a nullához.
Miért is? Legyen mondjuk 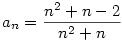 , ami szemlátomást szigorúan 0 és 1 közé esik, ha n legalább 2. Ekkor az an-ek szorzatának határértéke nem nulla lesz. Gyakorlásképpen, akinek van kedve, számolja ki a szorzat határértékét, mondjuk a 2. tagtól kezdve (n=1-re an=0, tehát úgy nem lenne túl nehéz szorzatot számolni). , ami szemlátomást szigorúan 0 és 1 közé esik, ha n legalább 2. Ekkor az an-ek szorzatának határértéke nem nulla lesz. Gyakorlásképpen, akinek van kedve, számolja ki a szorzat határértékét, mondjuk a 2. tagtól kezdve (n=1-re an=0, tehát úgy nem lenne túl nehéz szorzatot számolni).
|
| Előzmény: [772] Atosz, 2005-02-06 23:27:49 |
|
| [772] Atosz | 2005-02-06 23:27:49 |
 Kedves Kemény Legény!
Gratulálok a megoldáshoz! Ez tulajdonképpen egy ujjgyakorlat volt "szörnyűnek" tűnő megfogalmazásban. Szerintem azért ez egy érdekes tulajdonsága a súlypontnak. Azt viszont furcsálnám, ha 1-nél kisebb számok szorzata nem tartana a nullához.
|
| Előzmény: [771] Kemény Legény, 2005-02-06 19:48:18 |
|
| [771] Kemény Legény | 2005-02-06 19:48:18 |
 Legyenek az A0B0C0 csúcsaiba mutató helyvektorok:a,b,és c.Ekkor az A1 pont helyvektora kifejezhető a és b lin.komb.jaként,mégpedig ax+by alakban ahol x+y=1.Ekkor B1,C1 pontok helyvektorai: bx+cy ill.cx+ay lesznek. Az eredeti 3-szög súlypontja (a+b+c)/3,mig az új 3-szögé: (ax+by+bx+cy+cx+ay)/3=(a+b+c)(x+y)/3=(a+b+c)/3 lesz. Igy a müvelet során a háromszögek súlypontjai változatlanul maradnak,és mivel a háromszög súlypontja általában a belsejébe szokott esni,ezért ha a 3-szögek végtelen sorozata egyáltalán konvergál vmely ponthoz(elég ha a területük tart 0-hoz,mivel egymásba skatulyázott zárt halmazok),akkor az a háromszög súlypontja lesz.Az már persze nem geometriai kérdés hogy végtelen sok véletlenszerüen választott 0 és 1 közti szám szorzata milyen eséllyel tart 0-hoz,hiszen csak ekkor konvergálhat a 3-szögsorozat vhová.
|
| Előzmény: [770] Atosz, 2005-02-04 09:52:18 |
|
| [770] Atosz | 2005-02-04 09:52:18 |
 145. feladat Vegyünk egy tetszőleges A0B0C0 háromszöget, majd ennek A0B0 oldalán véletlenszerűen válasszunk ki egy pontot, legyen ez A1. Amilyen arányban felosztja A1 az A0B0 oldalt, ugyanilyen arányban (és megfelelő sorrendben) vegyük fel a B1 és C1 pontokat a megfelelő oldalakon. Így kapjuk az A1B1C1 háromszöget. Az eljárást kezdjük előlről (már az új háromszögön - újra véletlenszerű választással) és folytassuk a végtelenségig. A kérdés az, hogy a háromszögeknek ez a végtelen sorozata az eredeti háromszög mely belső pontjához konvergál?
|
|
| [769] Káli gúla | 2005-01-31 23:30:02 |
 A
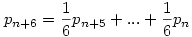
rekurzió megoldására gondoltam (bár elismerem, az "igazi" jelző kicsit erős volt :)
Nézzük, mi lenne, ha nem a (0,0, ... , 1) kezdeti feltételekkel indulnánk. Vegyük az (1,0,...,0)-hoz tartozó 1,0,...,0,1/6, . . . sorozatot. Az első elemet elhagyva a 0,..,0,1/6, . . . sorozatot kapjuk, tehát (1,0,..,0)-ról indulni pontosan ugyanaz, mint (0.0,...,1/6)-ról. Hasonló összefüggést kaphatunk a többi kezdeti feltételre is (felhasználva a megoldásoknak a kezdeti feltételtől való lineáris függését). Jelöljük a (0,..,1,..,0) j-edik egységvektorral induló megoldást Ej-vel. Tegyük fel, hogy létezik a keresett határérték (lim E6(n) = p). Legyen az első elem elhagyása (a léptetés operátor) T. Világos, hogy TEj(6) = Ej(7) = 1/6 (j=1,..,6), ezért
E1 TE1=1/6E6 TE1=1/6E6 1/6p 1/6p
E2 TE2=E1+1/6E6 TE2=E1+1/6E6 2/6p 2/6p
E3 TE3=E2+1/6E6 TE3=E2+1/6E6 3/6p 3/6p
E4 TE4=E3+1/6E6 TE4=E3+1/6E6 4/6p 4/6p
E5 TE5=E4+1/6E6 TE5=E4+1/6E6 5/6p 5/6p
E6 6/6p 6/6p
Ezeket összeadva, E1+...+E6 1 miatt 1 miatt
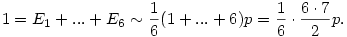
* * *
Be kell még látni, hogy minden megoldás konvergens. Ehhez felhasználhatjuk azt a tulajdonságot, hogy a számtani közép nem kerülhet túl közel a számhalmaz széléhez, pontosabban, ha a xj xj b (j=n+1,...,n+6), akkor a+d/6 b (j=n+1,...,n+6), akkor a+d/6 M M b-d/6, ahol d=b-a és M az xj (j=n+1,...,n+6) számok számtani közepe. Így, ha a sorozat elemeit hatosával blokkokra osztjuk, az egyes blokkok mindig az előző blokk által feszített intervallum középső kétharmadába esnek. b-d/6, ahol d=b-a és M az xj (j=n+1,...,n+6) számok számtani közepe. Így, ha a sorozat elemeit hatosával blokkokra osztjuk, az egyes blokkok mindig az előző blokk által feszített intervallum középső kétharmadába esnek.
|
| Előzmény: [768] Atosz, 2005-01-30 19:21:54 |
|
| [768] Atosz | 2005-01-30 19:21:54 |
 Kedves Káli gúla!
Köszönöm a gratulációt! Egyébként ez volt a te "igazi" megoldásod is, vagy a rekurziós?
|
|
| [767] Káli gúla | 2005-01-30 11:57:12 |
 Kedves Atosz, bocs, újraolvasva, teljesen jó ahogy írtad. Mindegy, hogy időben az első, vagy az utolsó mező szerint számolunk.
Kedves Kemény Legény, kösz a hivatkozást. A konvergencia bizonyítással a végén tényleg nem sokat epszilonozik.
|
|
| [766] Káli gúla | 2005-01-30 10:46:30 |
 Igen, grat! Annyi kiegészítéssel, hogy Ai az az esemény legyen, amikor utoljára mondjuk, hogy most már elég egy dobás.
Általánosabban, 6 helyett k-ra, egy k hosszú szakaszba való bekerülés valószínűsége egy. Az elhagyó (utoljára érintett) mező szerint osztályozva
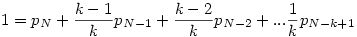
Így, ha tudjuk, hogy lim pN=p létezik, akkor
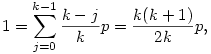
ahonnan p=2/(k+1), éppen a lépéshossz várható értékének a reciproka.
|
| Előzmény: [765] Atosz, 2005-01-30 08:22:27 |
|
| [765] Atosz | 2005-01-30 08:22:27 |
 Sziasztok!
Azt hiszem meg van a megoldás. Káli gúla hozzászólása ébresztett rá arra, hogy egy szomszédos 6-os tartományba lépés valsége nagyobb mint 1, hiszen ezek nem függetlenek egymástól. Az utolsó dobás alapján elkezdtem a rekurziót visszafejteni és kaptam, hogy
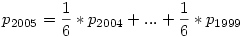
Ez azt jelenti, hogy a sorozat mindig az előző hat átlagával halad tovább és mivel az elejét ismerjük így onnan elindulva kiszámítható, hogy mennyi lesz p2005
Viszont ennél találtam egy gyorsabb megoldást is! Tekintsük azokat az eseményeket, amikor kimondom azt, hogy most már 1 dobással is beérhetek a célba. Ez 6 helyet jelent a 2005-ik előtt. Legyen Ai az az esemény, hogy a (2005-i)-ik helyen szólalok meg (i=1,...,6). Ezen események valségei pAi nem egyeznek meg a rálépés valségével, viszont függetlenek és összegük 1. Legyen ilyen távolságban a mezőre lépés valsége p (feltesszük, hogy már közel egyforma - éppen ezt keressük). A 2004-ik helyen akkor szólalok meg, ha előtte ráléptem az 1998-ikra és ott 6-ost dobtam, azaz 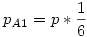 . A 2003-ik helyen akkor szólalok meg, ha az 1998-ik helyről érkezem 5-össel, vagy az 1997-ről 6-ossal, azaz . A 2003-ik helyen akkor szólalok meg, ha az 1998-ik helyről érkezem 5-össel, vagy az 1997-ről 6-ossal, azaz 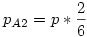 , stb... , stb...
Ha ezt mind felírjuk, kapjuk hogy
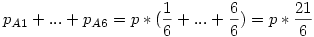
Mivel ez 1, így
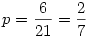
Természetesen ez csak akkor lesz pontosan igaz, ha a kérdéses hely tart a végtelenbe, de a 2005. már "jó közelítéssel" ennek tekinthető.
|
|
| [764] SAMBUCA | 2005-01-29 19:56:25 |
 Hali!
A Kemény Legény által emlegetett cikk megtalálható itt.
SAMBUCA
|
|
| [763] Kemény Legény | 2005-01-29 16:00:57 |
 Na a cikk a KöMaL elektronikus archivumában található meg,pl. rákeresve Kós Géza cikkeire,a Játék mindenkinek -et kiválasztva.A 11-es szám pedig a novemeber hónapot volt hivatott jelölni,kár hogy nem találtátok meg.
|
|
| [762] Atosz | 2005-01-29 13:25:05 |
 Bolond vagyok!
Az előző hozzászólásomat tekintsétek semmisnek, hiszen pont ez a lényeg, a pi-k összege nem 1.
|
|
|
| [760] Atosz | 2005-01-29 13:01:25 |
 Egy újabb gondolat jutott eszembe, s közben láttam Káli gúla a segítségedet. Mindjárt végiggondolom, de közben beírom azt, amit akartam:
Egy szomszédos 6-os tartományba lépés összvalsége 1 kell hogy legyen, azaz p(n-6)+p(n-5)+...+P(n-1)=1. De a mellette lévő 6-os tartományra is ennek igaznak kell lennie, azaz p(n-6)=p(n). Ebből az következik, hogy minden 6. mezőre lépésnél egyforma valségek vannak, azaz P(2005)=p(1)=
Ez vagy jó, vagy nem, de akkor hol van benne a hiba?
|
| Előzmény: [759] Káli gúla, 2005-01-29 11:58:15 |
|
|
| [758] Atosz | 2005-01-29 11:32:25 |
 Pontosan hol van az a cikk, mert nem találom?
Engem leginkább az zavar a saját megoldásomban, hogy ha a 2004, 2003, 2002, 2001 2000, 1999 helyek valamelyikén egyforma valséggel leszünk, akkor miért nem  jön ki a 2005-re? (mert akkor ugyanígy egyforma valséggel lennénk a 2005-2000 helyek valamelyikén is) jön ki a 2005-re? (mert akkor ugyanígy egyforma valséggel lennénk a 2005-2000 helyek valamelyikén is)
|
| Előzmény: [757] Kemény Legény, 2005-01-29 10:23:59 |
|
| [757] Kemény Legény | 2005-01-29 10:23:59 |
 Elnézést a közbeszólásért,de szerintem nem ennyi lesz a végeredmény és a megoldás sem ilyen egyszerű.De a legjobb lesz,ha elolvassátok Kós Géza cikkét az 1994/11. KöMaL-ban,ahol egy elég zuzó megoldást nyomat a problémára.
|
|
| [756] Atosz | 2005-01-29 09:53:17 |
 Én a következőképp okoskodtam (remélem jól).
A dobálások után mindenképpen elérjük azt a helyzetet, amikor azt mondhatjuk, hogy innentől akár egy dobással is nyerhetünk. Ekkor 1,2,3...,6 egység távolságra leszünk a 2005. rácsponttól. Az, hogy milyen valséggel állunk éppen az egyik vagy másik helyen, az "jó közelítéssel" egyformán valószínű, azaz  . (az origótól ekkora távolságban már az, hiszen ez a megfelelő távolságra lévő számok 1-6 számok összegeire való felbontások számától függ, ami közel egyforma) Innen a keresett valség . (az origótól ekkora távolságban már az, hiszen ez a megfelelő távolságra lévő számok 1-6 számok összegeire való felbontások számától függ, ami közel egyforma) Innen a keresett valség 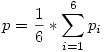
Itt már csak azt kell megvizsgálni, hogy egy adott távolságból hányféleképpen juthatunk célba. pl. 3 egység távolságból bejuthatunk a következő dobásokkal: (3) vagy (1,2) vagy (2,1) vagy (1,1,1). Egy egylépéses győzelem valsége  , míg egy k lépésesé , míg egy k lépésesé 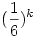 , hiszen k-szor egymás után megfelelőt kell dobnunk. Ha megfigyeljük a megfelelő távolságokról a bejutásokat, akkor látjuk, hogy éppen 6 egylépéses, 15 kétlépéses, 20 háromlépéses, 15 négylépéses, 6 ötlépéses és 1 hatlépéses győzelem van. Ezek a számok éppen a Pascal háromszög megfelelő sorának tagjai (az első 1-es kivételével). Így , hiszen k-szor egymás után megfelelőt kell dobnunk. Ha megfigyeljük a megfelelő távolságokról a bejutásokat, akkor látjuk, hogy éppen 6 egylépéses, 15 kétlépéses, 20 háromlépéses, 15 négylépéses, 6 ötlépéses és 1 hatlépéses győzelem van. Ezek a számok éppen a Pascal háromszög megfelelő sorának tagjai (az első 1-es kivételével). Így
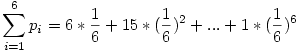
Ami a binomiális tétel szerint ez éppen:
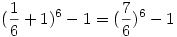
Így a keresett valség:
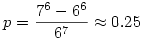
|
| Előzmény: [755] Káli gúla, 2005-01-27 23:18:19 |
|
| [755] Káli gúla | 2005-01-27 23:18:19 |
 Kösz. Én is a rekurziót oldottam meg először.
Erről eszembe jut egy feladat, szintén valszám, és szintén rekurzió, Amikor először hallottam, talán egy egész spirálfüzetet teleírtam, de nem tudtam megcsinálni. Évek múlva jöttem csak rá az "igazi" megoldásra.
144. feladat. Az origóból kiindulva a számegyenes pozitív rácspontjain lépkedünk. Minden lépés előtt feldobunk egy dobókockát, és annyit lépünk előre, amennyit a kocka mutat. Mi a valószínűsége (jó közelítéssel) annak, hogy rálépünk a 2005. rácspontra.
|
|
| [754] jenei.attila | 2005-01-27 21:06:27 |
 Szóval én úgy értelmezem Káli gúla modelljét, hogy kitüntetjük az őrültek helyét, és az utolsó helyet (feltesszük, hogy az utolsó utas nem őrült). Egy kísérlet abban ál, hogy beszállítjuk az összes utast, miközben feljegyezzük, hogy a kitüntetett helyeket milyen sorrendben foglalták el. Nyilván akkor ül az utolsó utas a helyére, ha az utolsó helyet jegyeztük fel utoljára. Egy kísérlet tehát a kitüntetett helyek permutációját adja, amelyek ha egyenlő valószínűséggel fordulnak elő, akkor az utolsó utas valóban 1/(k+1) valséggel ül a helyére. Az hogy ezek a permutációk egyenlő valószínűséggel fordulnak elő, azon múlik, hogy a kitüntetett még el nem foglalt helyek bármelyikét minden pillanatban amikor kitüntetett helyet foglal el egy utas, egyenlő valószínűséggel választja.
Káli gúlának gratulálok ehhez a megoldáshoz, az enyém sokkal körülményesebb. Csak az lenne a kérdésem, ha nem ismerted volna az eredményt, akkor is ezt a megoldást adtad volne-e?
|
| Előzmény: [753] Kós Géza, 2005-01-27 17:01:18 |
|
|
|






 TE1=1/6E6
TE1=1/6E6 1 miatt
1 miatt  xj
xj
