| [826] Atosz | 2005-03-06 18:38:23 |
 Sziasztok!
Már azt hittem, hogy senkit sem fog meg ez a különleges feladvány. A "csavar" Csimby gondolatában van, azt egy picit még tovább lehet fejleszteni. A szélsőérték-probléma nyilván az, hogy meddig menjen előre az első gyerek, meddig vigye vissza a kutya a bicajt, hogy végül mindhárman egyszerre érjenek be. Ennek kidolgozását azért rátok bízom.
A feladatnak egyébként komoly matek-irodalma van, hiszen azt hinnénk elsőre, hogy László megoldása nem javítható - és mégis (lásd Csimby) Ehhez persze meglepő módon viszafelé kellett bicajozni egy szakaszon.
1. Masuda, S. (1970). "The bicycle problem," University of California, Berkeley: Operations Research Center Technical Report ORC 70-35.
2. Chvatal, V. (1983). "On the bicycle problem," Discrete Applied Mathematics 5: pp. 165 - 173.
Remélem az előtte lévő feladatot is megoldjátok! Jó munkát!
|
|
| [825] Csimby | 2005-03-06 15:23:15 |
 Ha a kutya, mikor eléri az otthagyott biciklit, visszaviszi azt annak a gyereknek, aki addig sétált, akkor a gyerekek többet tudnak biciklizni az út felénél. Így nekem kijött egy megoldás, amivel kevesebb mint 2 óra 50 perc alatt megjárják az utat.
|
| Előzmény: [824] lorantfy, 2005-03-06 13:31:57 |
|
| [824] lorantfy | 2005-03-06 13:31:57 |
 Hello Atosz!
154. feladathoz: Ha a kutya nem biciklizik, csak végigsétál, akkor 2 óra 30 perc alatt teszi meg az utat. Jancsi és Juliska felesben használva a bicajt - hogy egyszerre érjenek be - 2 óra 30 perc séta + (5/12)*60=25 perc biciklizés után= 2 óra 55 perc alatt érnek be a célba.
Ha a kutya bicajozna, az csak növelné az időt, hiszen Jancsi és Juliska ezalatt lassabban haladna.
Nekem így túl egyszerűnek tűnik. Lehet hogy valamit félreértettem?
A kerékpár felesben való használatát úgy értettem, hogy pl. Juliska elmegy az út feléig. Ott letámasztja a bicajt egy fához és továbbindul gyalog. Mikor Jancsi odaér a bicajhoz, felpattan rá és azzal megy tovább.
Ha nem hagyhatják el a bicajt, hanem kézből-kézbe kell adni, akkor meg nem tudják vele csökkenteni a menetidőt és csak 5 óra alatt tudnak beérni.
Remélem van benne még valami csavar! Vagy csak az adatokat adtad meg rosszul?
|
| Előzmény: [821] Atosz, 2005-03-04 10:16:30 |
|
| [823] Atosz | 2005-03-04 19:48:42 |
 Szia Csimby!
Most, hogy visszanéztem, tényleg azt beszéltétek egymás közt nadorppal, hogy várakozunk, de nem vettem észre! (legalábbis nem volt eszemben) Mégegyszer bocsi!
|
| Előzmény: [822] Csimby, 2005-03-04 13:14:43 |
|
|
| [821] Atosz | 2005-03-04 10:16:30 |
 Nemrég feltettem [153.] számmal egy "egyszerű" egyismeretlenes egyenlettel is megoldható feladatot. Egyelőre még senki sem írt be megoldást, de addig is itt egy újabb érdekesség:
[154.] feladat Egy fiú, egy lány és egy kutya 10 km-es útra indulnak. A fiú és a lány 2 km/h-val haladnak, a kutya 4 km/h-val. Van azonban egy biciklijük, amit mind a hárman (a kutya is) használhatnak, de egyszerre csak az egyikük. A fiú és a lány 12 km/h-val tud biciklizni, a kutya 16 km/h-val. Mi az a legrövidebb idő, ami alatt mindhárman célba érnek?
|
|
| [820] Atosz | 2005-03-04 09:59:10 |
 Ha jól láttam Csimbynek ez a feladata (127) még megoldatlan. Nekem gyorsan kijött a harmonikus sor és a mértani közép közti egyenlőtlenség, illetve a harmonikus sor és a természetes logaritmus közti kapcsolat alapján. Tényleg nem volt nehéz.
|
| Előzmény: [804] Csimby, 2005-02-27 16:20:12 |
|
| [819] Atosz | 2005-03-02 14:36:37 |
 Szia Nadorp!
Kösz, hogy beláttad, szerintem egyből érezhető volt, hogy a két pont szerepe felcserélhető. Még próbálkozom vele, de egyelőre nincs általános megoldásom. Minden jót!
|
| Előzmény: [815] nadorp, 2005-03-02 08:26:40 |
|
| [818] Eduard Helly (1884-1943) | 2005-03-02 13:42:34 |
 Kedves Nadorp!
A kérdést egyáltalán nem személyeskedésnek szántam. (Tényleg nem állítottad, hogy Te találtad volna ki a feladatot.) Ha mégis így éreznéd, akkor bocs.
A feladat szép példa és jó gyakorlófeladat egy bizonyos tétel alkalmazására, de a tétel ismerete nélkül talán túlságosan nehéz. Ha megmondjuk, hogy kinek a tételéről van szó - egy hét után adhatunk ennyi segítséget -, akkor persze OK. ;-) .
E. H.
|
| Előzmény: [817] nadorp, 2005-03-02 11:39:54 |
|
| [817] nadorp | 2005-03-02 11:39:54 |
 Nem sportszerűtlen, hanem általános formájában nehéz. Sohasem állítottam [796], hogy magamtól oldottam meg, viszont egy középiskolásoknak is szóló szenzációs könyvben olvastam (Reimann: A geometria és határterületei).
|
| Előzmény: [816] Eduard Helly (1884-1943), 2005-03-02 09:41:15 |
|
|
| [815] nadorp | 2005-03-02 08:26:40 |
 Szia Atosz !
Igazad van, úgy látszik a példát nem értettem teljesen, de az egyértelműség miatt úgy fogalmaznám ( bár ez már csak "szőrszálhasogatás" ), hogy AP/BP 2 és BP/AP 2 és BP/AP 2. Egyébként az állítás igaz tetszőleges korlátos,zárt,konvex tartományra. 2. Egyébként az állítás igaz tetszőleges korlátos,zárt,konvex tartományra.
|
| Előzmény: [813] Atosz, 2005-03-01 21:52:49 |
|
| [814] xXx | 2005-03-01 23:40:27 |
 Kösz Csimby! Tetszik..:-)
|
|
| [813] Atosz | 2005-03-01 21:52:49 |
 Szia Nadorp!
Ha jól értem a feladat szövegét, akkor nekem egyenértékűnek tűnik a "középső harmadába esik" kitétel, illetve a Káli gúla által megadott arány, azaz egyiből köv. a másik és fordítva. Addig is amíg ezt kiderítjük, itt van a következő, a [153.] feladat. Ezt középiskolában a szöveges egyenletek végén célszerű bevetni, hogy értik-e a nebulók a témát:
[153.] feladat: A barátom és én, együtt 86 évesek vagyunk. Az én életkorom 15/16-a annak az életkornak, amennyi idős a barátom akkor lesz, amikor az én életkorom 9/16-a lesz annak az életkornak, amennyi idős a barátom akkor lenne, ha kétszer annyi idős lenne, mint én akkor, amikor életkorom éppen kétszerese az ő életkorának. Mennyi idős vagyok?
Természetesen mindezt tovább csűrni csavarni nem érdemes, hiszen rengeteg ilyet lehetne kreálni, de azért egynek nem rossz. Lehet próbálkozni az egyenlettel...
|
| Előzmény: [809] nadorp, 2005-03-01 08:16:01 |
|
| [812] nadorp | 2005-03-01 12:15:48 |
 Én sem arra gondoltam, hogy a becslés elegendő A365-höz, de ha valaki egy kicsit elkezdi élesítgetni egy hasonló módszerrel, mint amit - ezt csak sejtem - Te használtál, akkor abból már kijöhet valami.
|
| Előzmény: [811] Csimby, 2005-03-01 11:11:13 |
|
| [811] Csimby | 2005-03-01 11:11:13 |
 Hát jó, várjunk vele 15.-ig, bár én sajnos nem látom hogyan lehetne felhasználni A.365-ben. (persze lehet, hogy a bizonyításban van valami eszköz ami használható oda is...)
|
| Előzmény: [810] nadorp, 2005-03-01 08:30:18 |
|
|
| [809] nadorp | 2005-03-01 08:16:01 |
 Szia !
Ez nem ugyanaz, mint Káli guláé, mert ebből következik a 146. feladat állítása ( azaz elvileg erősebb az állítás). Azért csak elvileg, mert lehet, hogy ekvivalensek, ezt nem sikerült belátnom.
|
| Előzmény: [796] Atosz, 2005-02-26 08:08:21 |
|
| [808] Csimby | 2005-02-28 21:42:30 |
 A zöld szakaszok hosszának összege a háromszögegyenlőtlenség miatt (10-szer kell használni) nagyobb mint az oldalak hosszának összege.
A kék szakaszok hosszának összege a háromszögegyenlőtlenség miatt (10-szer kell használni) nagyobb mint az oldalak hosszának összege.
A piros szakaszok hosszának összege a háromszögegyenlőtlenség miatt (10-szer kell használni) nagyobb mint az oldalak hosszának összege.
Ha mindegyik lila szakaszt kétszer vesszük, akkor szintén a háromszög egyenlőtlenség miatt (10-szer kell használni) a hosszuk összege nagyobb mint az oldalak hosszának összege (mindegyik lila szakasz két olyan háromszögbe is beletartozik amelynek egyik oldala a 10-szög oldala, másik oldala pedig szintén lila szakasz).
Tehát a kék, zöld, piros és lila szakaszok hosszának a 2-szerese nagyobb mint az oldalak hosszösszegének a 7-szerese.
Világos, hogy a lila, kék, zöld, piros szakaszok hosszának az összege kisebb mint az átlók hosszának az összege. Tehát az átlók hosszösszegének 2-szerese nagyobb mint az oldalak hosszösszegének a 7-szerese. Az egyenlőtlenség mindkét oldalát 70-nel leosztva megkapjuk, hogy az oldalak hosszának számtani közepe kisebb mint az átlók hosszának számtani közepe (hiszen 10*7/2=35 átlója van).
Az ábrán csak esztétikai okokból szerepel szabályos 10-szög, könnyen végig gondolható, hogy a bizonyítás bármely konvex 10-szögre működik.
|
 |
| Előzmény: [807] xXx, 2005-02-28 19:01:59 |
|
| [807] xXx | 2005-02-28 19:01:59 |
 Üdv mindenkinek! Csimby kérésére még két házifeladat:-)
151.feladat: Az ABCDA'B'C'D' és EFGHE'F'G'H' egybevágó kockák. ACC'A' és EGG'E' átlós metszetének a sikja közös és ez a két téglalap közös középpontjuk körül 90 fokos elforditással egymásba vihető át. Fejezzük ki a kockák közös részének térfogatát az AB=a éllel.
152.feladat: Bizonyitsuk be hogy tetszőleges konvex tízszög oldalhosszainak számtani közepe kisebb, mintátlói hosszának számtani közepe.
Dávid
|
|
| [806] lorantfy | 2005-02-27 16:26:41 |
 Az egyesek helyén álló számjegy legyen x, akkor a 10-es helyiértéken álló x+5. A szám értéke: 10(x+5)+x, hiszen a tizes helyiértéken álló értéke 10-szeres. Hasonlóan a felcserélt számjegyű szám: 10x+(x+5). Ezek összege 143 és kész az egyenlet.
|
| Előzmény: [803] Suzy, 2005-02-27 15:59:51 |
|
|
| [804] Csimby | 2005-02-27 16:20:12 |
 Van még valakinek valami házifeladata holnapra? Tényleg NAGYON ÉRDEKESEK... mindenki írja be ide, aztán majd valaki megcsinálja helyette...
Más: 127. feladat Biz. be, hogy
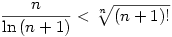
(saját, de nem valami nehéz és nem is ad túl jó becslést, ráadásul egyre pontatlanabb... azért érdekes lehet)
|
| Előzmény: [803] Suzy, 2005-02-27 15:59:51 |
|
| [803] Suzy | 2005-02-27 15:59:51 |
 Köszönöm.Sikerült. 3.Kétjegyű szám tízeseinek jegye 5-tel több mint az egyeseinek a száma.Ha a felcserélt számjegyű számot hozzáadjuk akkor 143-at kapunk.Mekkora az eredeti kétjegyű szám? Ez is egyenletben kéne.De a megoldást tudom.
|
|
| [802] lorantfy | 2005-02-27 15:28:39 |
 Legyen a gyerek most x éves, akkor az apa 3x. 50 év múlva mindketten 50 évvel lesznek idősebbek, tehát x+50 és 3x+50 évesek lesznek. Mivel ekkor az apa éveinek 1/4 részével idősebb a gyermekénél, így az apa életkorának 3/4-e pont a gyerek éveinek számát adja. Megvan az egyenlet!
|
| Előzmény: [801] Suzy, 2005-02-27 14:32:44 |
|







 2 és BP/AP
2 és BP/AP