| [411] Sirpi | 2004-07-14 21:35:09 |
 Még szerencse, hogy nem az a kérdés, Te mit tennél, hanem hogy a kalózok hogyan cselekednének :-). Nekik pedig, racionálisan gondolkodva, el kell fogadniuk az egy aranyat, ugyanis ellenkező esetben a következő kalóz SEMMIT nem adna nekik, tehát még rosszabbul járnának. Feltéve persze, hogy a kalózok nem játszanak össze, mindegyik csak a saját egyéni érdekeit nézi.
Tehát továbbra is fenntartom, hogy ha én kezdenék, 96 0 1 0 1 0 1 0 1 0-val indítanék.
Sirpi
|
| Előzmény: [410] Hajba Károly, 2004-07-14 15:46:41 |
|
| [410] Hajba Károly | 2004-07-14 15:46:41 |
 Kedves Sirpi!
Ha én lennék az 1 aranyas kalóz, bizony az osztó ellen szavaznék ... és zsupsz már a vízben is van.
Szerintem 4 kalóznak meg kell adnia az átlag 10-10 aranyat, hogy mindenképpen mellette szavazzanak, s ekkor már a többi 60 az övé lehet.
HK
|
| Előzmény: [409] Sirpi, 2004-07-14 11:22:59 |
|
| [409] Sirpi | 2004-07-14 11:22:59 |
 Mivel sokáig nem írt megoldást senki, leírom, mire jutottam.
Nézzük meg először, mi a helyzet 2 kalózra. Nyilván aki oszt, az mind a 100-at magának adja, és a másik hiába szavaz ellene, nem tehet semmit.
Három kalóz esetén ezért, ha az osztó a legutolsónak 1 aranyat ad, akkor már maga mellé állítja, mert ha az utolsó a vízbedobásra szavaz, nem kap semmit. Ilyenkor tehát 99 0 1 jó osztás.
4 kalóz esetén 99 0 1 0 megint megteszi (a 3. kalóz ekkor az első mellett fog szavazni, mert különben 0-t kapna, ezzel megvan az 50%).
Stb... 10 kalóz esetén 96 0 1 0 1 0 1 0 1 0 megfelelő leosztás (az egyeseknek érdemes megszavazni a dolgot, különben 0-t kapnának, azaz megvan az 5 szavazat).
Sirpi
Bár, amikor az első kalóz megteszi az ajánlatát, azért nem árt, ha picit aggódik, hogy nem fogtak-e össze néhányan ellene :-)
|
| Előzmény: [408] lorytibi, 2004-07-12 13:15:00 |
|
| [408] lorytibi | 2004-07-12 13:15:00 |
 Matek táborban az egyik tanárom adta fel ezt a feladatot, szerintem érdemes rajta elgondolkozni:
88. feladat: 10 kalóz szerzett 100 aranyat. Egymás közt el akarják osztani, úgy hogy a legkegyetlenebb kalóz osztja szét az aranyat, és ezt megszavaztatják. Ha a kalózok lagalább fele megszavazza, elosztják az ajánlat szerint. De ha a kalózok kevesebb, mint fele szavazza meg, a legkegyetlenebb kalózt vízbe dobják a nyílt tengeren, és a második legkegyetlenebb kalóz folytatja az elosztást. A kalózok egyformán inteligensek. Nincs köztük két egyformán kegyetlen. (A felosztó kalóz szavazata is beleszámít!)
Hány aranyat adjon magának a legkegyetlenebb kalóz, hogy biztosan ne dobják vízbe?
A feladatot lehet hogy nem fogalmaztam elég pontosan, de emlékezetből írtam le. Ha van valami kérdésetek írjatok!
|
|
|
|
| [405] nadorp | 2004-07-02 12:36:16 |
 Nem tudom,hogy szebb-e, de kicsit rövidebb.
Csináljunk az egyenletből egyenletrendszert:
log3(2x+1)=y és log2(3x-1)=y
azaz,
2x+1=3y
3x-1=2y
összeadva a két egyenletet 2x+3x=2y+3y. Mivel az f(x)=2x+3x függvény szigorúan monoton nő, ezért az előző egyenlőség csak x=y esetén teljesül, azaz
log3(2x+1)=x
2x+1=3x
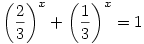
A fenti egyenletnek az x=1 megoldása,és másik nincs is, mert a bal oldalon egy szigorúan monoton csökkenő függvény áll.
|
| Előzmény: [404] Sirpi, 2004-07-02 11:50:23 |
|
| [404] Sirpi | 2004-07-02 11:50:23 |
 Nos, mivel eddig senki nem reagált senki a példára, beírom ide a ronda, favágós megoldásomat. Ha valaki tud szebbet, szóljon.
Legyen f(x)=log3(2x+1), g(x)=log2(3x-1). Olyan x-ek kellenek, amire f(x)=g(x).
Könnyű látni, hogy az x=1 megoldás, továbbá g(x) csak pozitív x-ekre van értelmezve. Ha ezek után megmutatjuk, hogy a közös értelmezési tartományon g(x) "gyorsabban nő", mint f(x), akkor készen is vagyunk, hiszen ebben az esetben az x=1-en kívül nem létezhet más megoldás.
Egyszerú átalakítással, felhasználva a logab=logcb/logca azonosságot, kapjuk, hogy 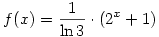 és és 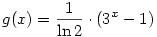 . .
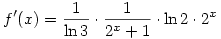
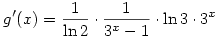
Mindkét derivált pozitív x>0 esetén, továbbá 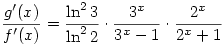 . Itt mindhárom tényező nagyobb, mint 1, vagyis minden x>0-ra g'(x)>f'(x), vagyis a g(x)-f(x) függvény szigorúan monoton nő. . Itt mindhárom tényező nagyobb, mint 1, vagyis minden x>0-ra g'(x)>f'(x), vagyis a g(x)-f(x) függvény szigorúan monoton nő.
|
| Előzmény: [403] lorantfy, 2004-06-30 06:50:07 |
|
| [403] lorantfy | 2004-06-30 06:50:07 |
 86. feladat: Oldjuk meg a köv. egyenletet a valós számok halmazán:
log3(2x+1)=log2(3x-1)
(Hegyi Lajos Emlékverseny 1999. 10.oszt.)
|
|
|
|
| [400] nadorp | 2004-06-28 10:18:27 |
 Újabb kísérlet a 85. feladatra.
Alakítsuk át az egyelet bal oldalát.
(x+y)2-4(x+y)+8y=13
(x+y-2)2=17-8y
Ha bevezetjük a z=x+y-2 jelölést, akkor (sajnos a frac nem működik)
y=(17-z2)/8 és
x=(z2+8z-1)/8.
Most már csak z-re kell kikötés. Látszik, hogy ha z páros, akkor y nem lehet egész, viszont ha z páratlan, akkor y - és így x is - egész lesz. Az egyenlet összes megoldása tehát a fenti két képlettel definiált x,y számok, ahol z tetszőleges páratlan szám.( pld x=8 y=-1 a z=5 esetén adódik)
|
| Előzmény: [397] lorantfy, 2004-06-28 09:19:12 |
|
| [399] Hajba Károly | 2004-06-28 09:57:14 |
 Kedves László és Péter!
Első ránézésre nem tűnt olyan érdekesnek, mint menet közben kiderült. :o)
Megoldás a 85. feladatra:
(1) (x+y)2-4(x-y)=13
Rendezzük y-ra az (1) egyenletet:
y2+2(x+2)y+x2-4x-13=0
azaz
y1,2=-(x+2) GYÖK(8x+17) GYÖK(8x+17)
Akkor kapunk egész megoldást, ha a gyök alatti érték négyzetszám. S itt meglepő fordulat következik. :o) Legyen
8x+17=(2n+1)2
 (n>1) (n>1) N+-re N+-re x. Azaz végtelen sok megoldás létezik. (Remélem jól írtam be a leírást. :o) x. Azaz végtelen sok megoldás létezik. (Remélem jól írtam be a leírást. :o)
Innen a képleteket (x=..., y=...) nem tudom beírni, mivel nem jó jelenleg a TeX értelmezője. :o(
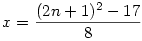
Később folytatom.
HK
|
| Előzmény: [395] lorantfy, 2004-06-27 12:54:37 |
|
| [398] nadorp | 2004-06-28 09:55:12 |
 Kedves László !
Teljesen igazad van, de mire ezt észrevettem, már Te is. A megoldásom teljesen rossz, elkapkodtam és elszámoltam. De vam másik, mindjárt leírom, ha még nem késő.
|
| Előzmény: [397] lorantfy, 2004-06-28 09:19:12 |
|
|
| [396] nadorp | 2004-06-28 08:35:24 |
 Úgyis régen szóltam hozzá. Megoldás a 85. feladatra.
Egészítsük ki az egyenlet bal oldalát teljes négyzetté.Ekkor
(x+y)2-4(x-y)+4(x-y)2=13+4(x-y)2
[x+y-2(x-y)]2=13+(2x-2y)2
(x-3y)2-(2x-2y)2=13
Két négyzetszám különbsége csak a 49 és 36 esetén lesz 13, ezért a
x-3y= 7 7
x-y= 3 3
egyenletrendszereket kell megoldani. Látható, hogy a négy egyenletrendszerből csak y=2 x=-1 esetén kapunk megoldást.
|
| Előzmény: [395] lorantfy, 2004-06-27 12:54:37 |
|
| [395] lorantfy | 2004-06-27 12:54:37 |
 85. feladat: Oldjuk meg az egész számok halmazán a következő egyenletet:
(x+y)2-4(x-y)=13
|
|
| [394] Lóczi Lajos | 2004-06-24 12:55:57 |
 Kedves Mihály!
Ahhoz, hogy egy valós függvény deriváltját a 0-ban kiszámolhassuk, szükséges, hogy a függvény értelmezve legyen legalább egy 0-hoz torlódó pontsorozat mentén.
Nem beszélhetünk tehát "csak az origóban deriválható függvényről, amely ott ráadásul kétszer is deriválható", hiszen a második derivált 0-beli értékének kiszámításához az előző bekezdés értelmében ismernünk kellene az első derivált értékeit egy 0-hoz torlódó pontsorozat mentén. Mivel azonban az első derivált csak a 0-ban van definiálva, ez nem lehetséges.
A válasz tehát, hogy ilyen függvény nincs.
|
| Előzmény: [393] Fálesz Mihály, 2004-06-18 14:06:40 |
|
| [393] Fálesz Mihály | 2004-06-18 14:06:40 |
 Mutassunk példát olyan valós függvényre, ami csak a 0-ban differenciálható, de ott kétszer is.
|
|
|
| [391] Sirpi | 2004-06-17 16:38:57 |
 Komplex számok ismerete nélküli megoldásként én arra gondoltam...
Igen, ez az egyszerű, de a második hozzászólásomban erre már én is rájöttem :-)
Az alapállítást f(1)=-1 jelenti, csak (*)-ból nem jöhet ki az állítás.
Teljesen jogos, pontatlanul fogalmaztam. A megoldás vázlata kb. így néz ki:
f(k+3)=f(k)f(3)-f(k-3)=2f(k)-f(k)=f(k), kihasználva az indukciót, a (*) összefüggést, valamint azt, hogy f(3)=2. Utóbbi pedig könnyen látszik, még ha nem is közvetlenül számolunk, akkor is: f(2)=f(1)f(1)-f(0)=1-2=-1, f(3)=f(1)f(2)-f(1)=(-1)2-(-1)=2
Tudom, túlragoztam a dolgot...
|
| Előzmény: [390] lorantfy, 2004-06-17 16:01:24 |
|
| [390] lorantfy | 2004-06-17 16:01:24 |
 Szia Sirpi!
Tetszik az f(k) függvényed! Az alapállítást f(1)=-1 jelenti, csak (*)-ból nem jöhet ki az állítás.
Komplex számok ismerete nélküli megoldásként én arra gondoltam, hogy mivel a=1 nem megoldása az egyenletnek, be lehet szorozni mindkét oldalt (a-1)-el.
Így (a-1)(a2+a+1)=0 vagyis a3-1=0 és ha a3=1 akkor persze a2004=1, tehát a keresett kifejezés értéke 2.
Persze a megoldás elég "misztikus" annak aki a komplex számokat nem ismeri. Hogy lehet az, hogy a 1 és a3=1? 1 és a3=1?
|
| Előzmény: [388] Sirpi, 2004-06-17 13:01:13 |
|
| [389] Sirpi | 2004-06-17 15:08:06 |
 Lehet, hogy elbonyolítottam...
0=0(a-1)=(a2+a+1)(a-1)=a3-1, ahonnan a3=1. Innen pedig a2004=(a3)668=1, ennek a reciproka is 1, összegük 2, ez tehát a végeredmény. Hogy minek gépeltem az előbb ennyit???
|
| Előzmény: [388] Sirpi, 2004-06-17 13:01:13 |
|
| [388] Sirpi | 2004-06-17 13:01:13 |
 Ez a 84. feladat poénos. A valós számok korében ugyanis nem teljesül a kezdeti feltétel, hiszen 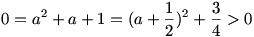 , de ettől pl. a komplex számok körében meg lehet a feladatot oldani. , de ettől pl. a komplex számok körében meg lehet a feladatot oldani.
Viszont az is meg tudja oldani a feladatot, aki nem is hallott a komplex számokról.
Vezessük be a következő jelölést: f(k)=ak+a-k.
Ekkor f(k)f(l)=(ak+a-k)(al+a-l)=(ak+l+a-(k+l))+(ak-l+a-(k-l))=f(k+l)+f(k-l)
Vagyis: f(k+l)=f(k)f(l)-f(k-l) (*)
Mi éppen f(2004)-et akarjuk kiszámolni. Amit tudunk a fenti összefüggésen kívül, az az, hogy f(0)=2, f(1)=-1 és f(k)=f(-k) minden egész k-ra.
Állítás: f(k+3)=f(k) minden k-ra, ez indukcióval bizonyítható a (*) összefüggésből (ezt a részt, ami nem is túl nehéz, rábízom másra). Innen f(2004)=f(0)=2.
/persze tudom, hogy a egy harmadik egységgyök, és innen triviálisan kijön a 2, mint megoldás, de elemi módszerekkel próbáltam a feladatot megoldani./
|
| Előzmény: [387] lorantfy, 2004-06-17 11:35:20 |
|
| [387] lorantfy | 2004-06-17 11:35:20 |
 84. feladat: Ha a2+a+1=0, akkor mennyi az értéke a
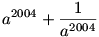
kifejezésnek?
|
|






 +sinSBC
+sinSBC
 GYÖK(8x+17)
GYÖK(8x+17)  (n>1)
(n>1) N+-re
N+-re x. Azaz végtelen sok megoldás létezik. (Remélem jól írtam be a leírást. :o)
x. Azaz végtelen sok megoldás létezik. (Remélem jól írtam be a leírást. :o) 

 1 és a3=1?
1 és a3=1?