Fórum: Matematikai Diákolimpia

[1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15]

Szeretnél hozzászólni? Jelentkezz be.

2008-07-16 16:30:30

2008-as spanyolországi matematikai olimpia első napjának feladatai:

1. Legyen H egy ABC hegyesszögű háromszög magasságpontja. $\gamma$ _A kör középpontja a BC oldalfelezőpontja, és átmegy H-n, BC oldalt A₁ és A₂ pontokban metszi. Hasonlóan definiáljuk a B₁,B₂,C₁,C₂ pontokat. Mutassuk meg, hogy A₁,A₂,B₁,B₂,C₁,C₂ egy körön vannak.

2. x,y,z valós számok mindegyike különbözik egytől és xyz=1. Mutassuk meg, hogy 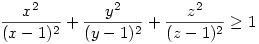$\frac {x^2}{(x-1)^2}+\frac {y^2}{(y-1)^2}+\frac {z^2}{(z-1)^2}\geq 1$ . Továbbá, hogy végtelen sok x,y,z racionális számhármasra az egyenlőtlenség egyenlőséggel teljesül.

3. Mutassuk meg, hogy végtelen sok pozitív egész n számra n²+1-nek van 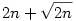$2n+\sqrt {2n}$ -nél nagyobb prímosztója.

[43] Sirpi	2006-08-07 13:36:41
Az M-et a megfelelő helyre beszúrtam, a hiányzó abszolútérték-jellel együtt.
Előzmény: [42] sakkmath, 2006-08-07 11:49:30

[42] sakkmath	2006-08-07 11:49:30
A képlet ugyanis hiányos! A helyes változat: az egyenlőtlenség bal oldalán álló kifejezés abszolútértékjelek között áll, a jobb oldali kifejezést pedig M-mel kell szorozni. Egyébként a mostani IMO honlapján is meg lehet találni a kitűzött feladatok magyar szövegét. A megoldásokat már csak angolul közlik. Üdv Mindenkinek!
Előzmény: [41] nadorp, 2006-08-07 11:17:44

[41] nadorp	2006-08-07 11:17:44
Az I/3 példában nincs M-re való hivatkozás a feltételek közt.
Előzmény: [40] Kós Géza, 2006-08-07 11:03:56

[40] Kós Géza

2006-08-07 11:03:56

A feladatok.

Első nap

1. feladat. Az ABC háromszög beírt körének középpontja legyen I. A háromszög P belső pontja kielégíti a PBA $\angle$ +PCA $\angle$ =PBC $\angle$ +PCB $\angle$ egyenlőséget. Bizonyítsuk be, hogy AP $\ge$ AI, és egyenlőség akkor és csak akkor áll fenn, ha P=I.

2. feladat. Legyen P egy szabályos 2006-szög. P egy átlóját jónak nevezzük, ha a végpontjai P határát két olyan részre bontják, amelyek mindegyike P páratlan sok oldalát tartalmazza. Az oldalakat szintén jónak nevezzük. Tegyük fel, hogy P-t háromszögekre bontottuk 2003 olyan átlóval, amelyek közül semelyik kettőnek nincs közös pontja P belsejében. Határozzuk meg az ilyen felbontásokban előforduló egyenlőszárú, két jó oldallal rendelkező háromszögek számának maximum át.

3. feladat. Határozzuk meg a legkisebb olyan M valós számot, amire az

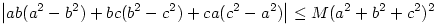
$\left| ab(a^2-b^2) + bc(b^2-c^2) + ca(c^2-a^2) \right| \le M(a^2+b^2+c^2)^2$

egyenlőtlenség teljesül minden a,b,c valós számra.

Második nap

4. feladat. Határozzuk meg az összes olyan, egész számokból álló (x,y) számpárt, amire teljesül 1+2^x+2^2x+1=y².

5. feladat. Legyen P(x) egy egész együtthatós, n>1 fokú polinom, és legyen k egy pozitív egész. Tekintsük a Q(x)=P(P(...P(P(x))...)) polinomot, ahol P k-szor fordul elő. Bizonyítsuk be, hogy legfeljebb n darab olyan t egész szám van, amire Q(t)=t.

6. feladat. Egy P konvex sokszög mindegyik b oldalához hozzárendeljük a legnagyobb területű olyan háromszög területét, aminek egyik oldala b és ami benne van P-ben. Bizonyítsuk be, hogy a P oldalaihoz rendelt területek összege legalább a kétszerese P területének.

Előzmény: [39] Kós Géza, 2006-08-07 10:46:46

[39] Kós Géza

2006-08-07 10:46:46

Úgy látom, a matekolimpikonok kicsit szégyenlősebbek, mert idén nem csillog annyira fényesen az eredmény (de azért mindenki nyert érmet).

	1.	2.	3.	4.	5.	6.	összesen	érem
Kis Gergely	7	3	1	6	7	0	24	ezüstérem
Jankó Zsuzsanna	7	7	0	6	3	0	23	ezüstérem
Erdélyi Márton	7	7	0	7	1	0	22	ezüstérem
Nagy Csaba	7	1	0	6	5	0	19	ezüstérem
Paulin Roland	7	4	0	7	1	0	19	ezüstérem
Tomon István	7	1	0	6	1	0	15	bronzérem

Estélyi István (Szolvákia)	7	1	0	7	0	0	15	bronzérem

Csapatban tizenhetedikek lettünk.

Az eredmények részletesebben itt olvashatók.

[38] rizsesz	2005-08-25 13:17:41
Ja nem :) én úgy gondoltam, hogy kik az idei versenyzők, csak kétféle módon kérdeztem rá, én okos. Agysejtek rulez! És gratula n+1. alkalommal.
Előzmény: [30] Zsuzsy, 2005-07-23 22:20:21

[37] SAMBUCA

2005-08-25 11:38:37

CSáttok Arcok!

GRATULA MINDENKINEK!!!!!!!!!!!!!

Üdv. SAMBUCA ( egy ex HUN1 :P)

[36] Zsuzsy	2005-08-07 18:58:30
Danke, de mi az hogy Alk.?

[35] Edgar

2005-07-30 22:20:17

fizikus csapat == arc. szerintem.

Kár, hogy 1 ponton múlt a 3 magyar arany a matek nyesőn. Nem baj, jövőre Alk. Zsuzsi biztos kivágja a sárgarezet. Roller pedig alap :-D

Edgar 2004/5. példájában nem vitatható pont volt, hanem tetemes lyuk :-D Kétoldalról-csinálós-középen-elsumákolós. Szerintem. Valódi 42 pont azért nem könnyű biznissz, nemcsak mindent meg kell csinálni rendesen, de jó gyorsan is, és aztán tisztán leírni... le a kalappal azelőtt, aki nem koordinátori (javítói) hibából éri el ;-) A 42 ponttal való problémákat talán nem lehet jobban jellemezni, mint hogy az 1997-es aranycsapat két 41-et és egy 40-et is kapott...

[34] Edgar

2005-07-30 22:10:21

2005-ös csapat = arc! Gratulálok! Csak amiatt vagyok kicsit bánatos, hogy ezek szerint nem volt túl hatékony az egyenlőtlenséges arzenál by Davids :'( El kellett volna mondanom a Muirhead-et!! Ha jól tudnék TeX-ben szedni, már fellőttem volna valahova. Ha még nem nyestem volna be, ez egy jókis oldal, tudtommal az egyetlen, ahol a részletes eredmények is ottfeszülnek régi olimpiákról: http://www.srcf.ucam.org/ jsm28/imo-scores/ Innen megtudható, kik milyen azonosítót viseltek, és pontosan mikre kapták a pontokat. 2005 Mérida még nincs rajta :-(

[33] rizsesz	2005-07-26 13:47:54
Hát a fizikások is a papírforma szerint teljesítettek gondolom :) Illetőleg ott egy magyar diák, Halász Gábor holtversenyben a legtöbb pontot szerezte az abszolút versenyben! http://www.sulinet.hu/tart/cikk/ab/0/27409/1 Nekik is nagyon nagy gratula!

[32] Hajba Károly

2005-07-25 13:39:05

Én is gratulálok a csapatnak, főleg hogy megint vannak a fórumon is szereplők a csapatban.

Ui: Mi a helyzet a fizikásokkal? Volt, nem volt diákolimpia?

[31] Yegreg

2005-07-24 21:18:21

Én csatlakoznék Doom-hoz... Gratulálok minden versenyzőnek!

Üdv:

Yegreg

[30] Zsuzsy

2005-07-23 22:20:21

Elég tudni, hogy a kódolás névsor szerint történt, úgyhogy ha felírod a tavalyi résztvevőket, megfejtheted...

És köszi a gratulációt mindenkinek :))

Előzmény: [25] rizsesz, 2005-07-19 03:24:21

[29] Doom

2005-07-22 17:12:34

GRAT MINDENKINEK!!!

Azt hiszem, minimum ennyit megérdemelnek mindenkitől... :)

[28] Observer A

2005-07-19 10:30:55

Szerintem Rolandnak jövőre meg kellene céloznia a 42 pontot. Egy olyan feladaton csúszott el, ami a többieknek jól ment. Elég bosszantó lehet neki. Ezzel nem azt akarom mondani, hogy 42 pontot el kell érni, mert ez nagyon sok apróságon is múlik, de azért mint célt ki lehetne tűzni.

* * *

Tavaly Athénban, amikor a verseny már megvolt, de pontszámok még nem, és még nem lehetett tudni, hogy Edgarnak 39, 40, 41 vagy 42 pontja lesz (az 5. feladatra adott megoldása egy ponton vitatható volt), mondtam neki, hogy neki a harmadik olimpiáján illene 42 pontot szereznie. Egy pillanatra megállt, majd rám nézett, és halkan azt mondta: "Te szemét." :-)))

Előzmény: [27] Kós Géza, 2005-07-19 10:19:27

[27] Kós Géza

2005-07-19 10:19:27

	1.	2.	3.	4.	5.	6.	Összesen	díj
Paulin Roland (HUN4)	7	7	7	7	7	3	38	I. díj
Strenner Balázs (HUN6)	7	7	0	7	7	7	35	I. díj
Jankó Zsuzsa (HUN2)	7	7	0	7	6	7	34	II. díj
Steller Gábor (HUN5)	7	7	0	7	0	7	28	II. díj
Erdélyi Márton (HUN1)	7	7	0	7	0	6	27	II. díj
Mánfay Máté (HUN3)	7	3	0	2	7	0	19	III. díj
Összesen	42	38	7	37	27	30	181

Előzmény: [26] Hraskó András, 2005-07-19 03:47:11

[26] Hraskó András

2005-07-19 03:47:11

Ha jól emlékszem, ez a 2005. évi olimpiai csapat:

Erdélyi Márton, Bp., Fazekas, 11. évf.

Jankó Zsuzsa, Szeged, Radnóti, 11. évf.

Mánfay Máté, Bp., Fazekas, 12. évf.

Paulin Roland, Bp., Fazekas, 11. évfolyam

Steller Gábor, Bp., Radnóti, 12. évf.

Strenner Balázs, Székesfehérvár, Teleki, 12. évf.

[25] rizsesz

2005-07-19 03:24:21

Azt lehet tudni, hogy kik szerepeltek a tavalyi HUN1, HUN2... helyett, illetve kik a bitorlók?

rizsesz :)

[24] lorantfy	2005-07-18 21:03:42
Gratulálok a magyar csapat tagjainak és a felkészítő tanároknak! Nem találtam az országok rangsorát, így gyorsan kigyűjtöttem az élmezőnyt:

Előzmény: [23] Hraskó András, 2005-07-18 14:24:09

[23] Hraskó András

2005-07-18 14:24:09

Az idei olimpia a mexikói Meridában van a Yucatán félszigeten. A verseny már meg is volt, a csapat a még nem hivatalos eredmény szerint 9. lett. Gratulálhatunk nekik, ez remek eredmény.

A verseny honlapja: http://erdos.fciencias.unam.mx/index.htm.

A feladatok angolul: 1. nap, 2. nap.

Az eredmények itt olvashatók.

Infók az épp arrafelé járó Emily hurrikánról (ha jól értem kissé arrébb megy).

[22] Observer A	2004-12-02 12:23:33
Azok a képeim vannak, amiket Athénban már láttatok. Íme egy Mükénéből. A tavalyi eforiei edzőtáborból is szolgálhatok néhánnyal.

Előzmény: [17] SAMBUCA, 2004-11-30 15:53:15

[21] SAMBUCA	2004-11-30 21:04:31
OK, majd megdummer. CSa, SAMBUCA.
Előzmény: [20] Kemény Legény, 2004-11-30 20:58:51

[20] Kemény Legény	2004-11-30 20:58:51
Csa!HUN3 szerint is jo volna feltenni meg par kepet,persz termeszetesen némi cenzura utan.Elore is kosz 30HUN3.
Előzmény: [17] SAMBUCA, 2004-11-30 15:53:15

[1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15]

Már regisztráltál?
Új vendég vagy?