Fórum: Valaki mondja meg!

[1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] [84] [85] [86] [87] [88] [89] [90] [91] [92] [93] [94] [95] [96] [97] [98] [99] [100] [101] [102] [103] [104] [105] [106] [107] [108] [109] [110] [111] [112] [113] [114] [115] [116] [117] [118] [119] [120] [121] [122] [123] [124] [125] [126] [127] [128] [129] [130] [131] [132] [133] [134] [135] [136] [137] [138] [139] [140] [141] [142] [143] [144] [145] [146] [147] [148] [149] [150] [151] [152] [153] [154] [155] [156] [157] [158] [159] [160] [161] [162] [163] [164] [165] [166] [167] [168] [169] [170] [171] [172] [173] [174] [175] [176] [177] [178] [179] [180] [181] [182] [183] [184] [185] [186] [187] [188] [189] [190] [191] [192] [193] [194] [195] [196] [197] [198] [199] [200] [201] [202] [203] [204] [205] [206] [207] [208] [209] [210] [211] [212] [213] [214] [215] [216] [217] [218] [219] [220] [221] [222] [223] [224] [225] [226] [227] [228] [229] [230]

Szeretnél hozzászólni? Jelentkezz be.

[1860] Lóczi Lajos

2013-05-07 17:23:59

Az nem lenne jó, ha itt mindkettőnknek igaza lenne és a területet kétféleképpen is lehetne definiálni.

Konkrétan, melyik részlépéssel nem értesz egyet a levezetésemben? Továbbá képzeljük azt, hogy az egyik processzor a bal oldali területet számolja ki, a másik pedig a jobb oldalit: az egyik nem tud arról, hogy a másik "ugyanannyira közelíti-e a 0-t".

Mi legyen a megoldás?

Előzmény: [1859] polarka, 2013-05-07 17:18:23

[1859] polarka

2013-05-07 17:18:23

Mindkettőnknek!?

Az nyilván igaz, hogy [-1,0) között a fv -1 szerese a (0,1] közötti részének, tehát előjeles összegük 0-ra kell kijöjjön, ha ugyanannyira közelíted a 0-t mindkét oldalról. Ha pedig a feltétel nem teljesül, akkor nyilván nem lesz 0.

Előzmény: [1858] Lóczi Lajos, 2013-05-07 16:53:33

[1858] Lóczi Lajos

2013-05-07 16:53:33

Akkor viszont ellent kell mondjak Neked, mert szerintem a terület

$\int_{-1}^1 \frac{1}{x}dx=\int_{-1}^0 \frac{1}{x}dx+\int_{0}^1 \frac{1}{x}dx=\lim_{\delta\to 0^+}\int_{-1}^{-\delta} \frac{1}{x}dx+\lim_{\delta\to 0^+}\int_{2\delta}^{1} \frac{1}{x}dx=\lim_{\delta\to 0^+}(\ln|\delta|-\ln|2\delta|)=-\ln{2}.$

Most akkor kinek van igaza?

Előzmény: [1857] polarka, 2013-05-07 16:36:30

[1857] polarka	2013-05-07 16:36:30
Igen.
Előzmény: [1856] Lóczi Lajos, 2013-05-07 16:13:32

[1856] Lóczi Lajos

2013-05-07 16:13:32

Egyetértek, a cél nyilván az, hogy ezeket a formulákat pl. területszámításra használjuk. De akkor meg kell kérdezzem, hogy a korábbi c₁=c₂=c választással kapott primitívfüggvény-sereg megfelel-e a területszámítási intuíciónknak:

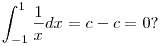
$\int_{-1}^{1}\frac{1}{x}dx=c-c=0?$

Vagyis ebben a példában a szimmetrikus területet valóban 0-nak szeretnénk definiálni?

Előzmény: [1855] polarka, 2013-05-07 16:06:46

[1855] polarka

2013-05-07 16:06:46

Talán, mert ha majdan függvény alatti területként szeretné valaki használni, akkor a következő határozott integrált kapnánk 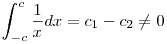$\int_{-c}^{c} \frac{1}{x} dx=c_1-c_2\ne 0$ , ahol c $\in$ R⁺

Ami nem felelne meg a területszámítási intuíciónak.

Előzmény: [1854] Lóczi Lajos, 2013-05-07 15:17:27

[1854] Lóczi Lajos

2013-05-07 15:17:27

Akkor -- továbbra is csak a valós számok körében maradva -- azt kérdezném, hogy mi az oka annak, hogy számos integráltáblázatban azt látom, amit írtál, miszerint

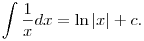
$\int \frac{1}{x} dx=\ln |x| +c.$

Azt írod, hogy az értelmezési tartomány legyen a maximális, azaz a 0-tól különböző valósok halmaza. Ha lerajzoljuk ezeket a függvényeket, akkor látszik, hogy mind tengelyesen szimmetrikusak. Én mondok egy bővebb függvényosztályt eredményül:

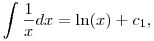
$\int \frac{1}{x} dx=\ln(x) +c_1,$

ha x>0, és

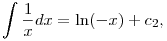
$\int \frac{1}{x} dx=\ln(-x) +c_2,$

ha x<0. Vagyis itt a két ág függőleges eltolása már nem feltétlenül ugyanaz.

Miért nem ezt a bővebb osztályt szokták akkor a könyvek feltüntetni?

Előzmény: [1851] polarka, 2013-05-07 10:52:50

[1853] polarka

2013-05-07 11:56:53

De ezen értékek csak a képzetes részt befolyásolják. Nem látom, hogy miért lenne probléma, ha tudok arról is, hogy az illető milyen úton (jelen esetben hányszor kerüli meg az origót és mekkora két pont közötti szögtávolság).

Mert én úgy látom, hogy az integrál felfogható úgy mint, egy vektor-vektor fv-ben végzett mozgás során végzett vonalintegrál. Ahol a valós rész a szokásos skalárszorzatot, a képzetes rész pedig a vektoriális szorzat értékét hordozza.

Előzmény: [1852] Alma, 2013-05-07 10:58:12

[1852] Alma	2013-05-07 10:58:12
Az a probléma (határozott integrálban gondolkodva), hogy míg valósban két szám között csak egyféle szakaszon tudsz integrálni (a valós tengely megfelelő részén), a komplex síkon két számot különböző görbékkel tudsz összekötni. Így c₁ és c₂ közötti határozott integrált több különböző görbén is értelmezheted, és sajnos ezek bizonyos függvényeknél különböző értékeket adhatnak. Ha a függvényednek nincs pólusa, akkor a különböző görbéken elvégzett integrálok értékei megegyeznek. Az 1/x függvénynek van pólusa x=0-ban.
Előzmény: [1851] polarka, 2013-05-07 10:52:50

[1851] polarka

2013-05-07 10:52:50

De R $\subset$ C, így amit leírtam $\varphi$ =0 vagy $\pi$ (+k2 $\pi$ ) esetén visszaadják a valós értelmezést (annál kicsit többet a fázisok miatt). k $\in$ Z; r $\in$ R⁺; $\varphi$ $\in$ R

Ha x $\in$ R\{0}-ra szorítkozunk, és értékkészletnek is R-et vesszük, akkor az előzőkből Re( $\sim$ )-vel adódik:

$\sim$ =ln |x|+c

Előzmény: [1849] Lóczi Lajos, 2013-05-07 07:01:45

Már regisztráltál?
Új vendég vagy?