| [631] sakkmath | 2008-10-07 11:40:12 |
 Szia! Ez a feladat a The American Mathematical Monthly 2008/júniusi számában jelent meg azzal a "kis" különbséggel, hogy az egyenlőtlenséget az összes valós t-re és az összes   2-re kell bebizonyítani. 2-re kell bebizonyítani.
A megoldásokat a Monthly 2008. október 31-ig kéri a nyomtatott lapban közölt címre. Ez arra utal, hogy (üzleti okokból) elsősorban a lap vásárlóitól várják a megoldásokat. Ezek miatt úgy vélem, az lenne a helyes, ha az esetleges megoldó csak november 1-től tenné nyilvánossá a megoldását bárhol, s így pl. itt, a Fórumban is. Alább mellékelem az interneten talált, idevágó laprészletet.
(Az Érdekes matekfeladatok [2727]-es hozzászólásában általad közölt feladat szintén "él" és egy másik matematikai MAGAZIN várja a megoldását 2008. november 1-ig.)
Üdvözlettel: sakkmath
|
 |
| Előzmény: [602] Gyöngyő, 2008-09-28 13:55:06 |
|
|
| [629] Róbert Gida | 2008-10-06 22:51:05 |
 Nem írtad, de feltételezem, hogy T a természetes egészeken van értelmezve, így a,b 0-t is feltehetem. 0-t is feltehetem.
1. eset: a+b<1. Tetszőleges N0 egészre és elég nagy d számra telejesül, hogy T(n) d*n minden n<N0-ra. Legyen most d*n minden n<N0-ra. Legyen most 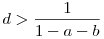 és még olyan nagy, hogy az előbbi feltétel is teljesül, azaz T(n)<d*n, ha n<N0 és még olyan nagy, hogy az előbbi feltétel is teljesül, azaz T(n)<d*n, ha n<N0
Indukcióval tegyük fel, hogy k<n-re T(k) d*k. Ekkor k=n-re is teljesül ez: a feltételt használva: T(n) d*k. Ekkor k=n-re is teljesül ez: a feltételt használva: T(n) n+T(an)+T(bn) n+T(an)+T(bn) n+adn+bdn=(1+d(a+b))n n+adn+bdn=(1+d(a+b))n dn teljesül, mert d(1-a-b)>1 igaz, d-re tett feltevés miatt. dn teljesül, mert d(1-a-b)>1 igaz, d-re tett feltevés miatt.
2. eset: Ha a+b>1, akkor létezik olyan c>1 valós szám, melyre T(n)=nc-vel definiált sorozat esetén T teljesíti a feltételt, továbbá T nyilván nem lineáris (mert c>1). c egyébként az a szám, melyre, ha a,b<1, akkor ac+bc=1 teljesül, ha a 1 vagy b 1 vagy b 1, akkor tetszőleges c>1 jó. 1, akkor tetszőleges c>1 jó.
3. eset Ha a+b=1, ekkor nem tudom mi van.
|
| Előzmény: [623] Algo, 2008-10-06 16:51:21 |
|
| [628] Doom | 2008-10-06 22:47:36 |
 Szia!
Igen, jól gondolkodsz. Annyi megjegyzést fűznék hozzá, hogy figyeld meg a Fibonacci sorozat kialakulását, ez még sokszor jól jöhet...
|
| Előzmény: [627] Algo, 2008-10-06 21:09:15 |
|
| [627] Algo | 2008-10-06 21:09:15 |
 Kedves Jonas és Doom!
A feladat ismertetése előtt 2-es számrendszerben próbáltam felírni a számokat, s ehhez társítani az optimális pénzmennyiséget. Ötleteteket végiggondoltam, s valóban 8 Ft felhasználásával meg tudom mondani, melyik számra gondolt. Egyfajta önmagamat is meggyőzésképpen: 1Ft---> 1 szám 2FT---> 2 szám 3Ft---> 3 szám 4Ft---> 5 szám 5Ft---> 8 szám 6Ft---> 13 szám 7Ft---> 21 szám 8Ft---> 34 szám
A megfelelő pénzek esetén visszavezetjük egy korábbi estre(pl.: 6Ft-ra úgy jön a 13 szám, hogy 8-5 arányban osztjuk szét, s 8 számhoz pedig legfeljebb 5 Ft-ra van szükségem)
Még egyszer köszönöm Jonasnak és Doomnak, hogy ötletüket megosztották.
Üdv.:Algo
Ui.: Remélem helyes a gondolatmenetem.:)
|
|
|
| [625] Doom | 2008-10-06 20:18:23 |
 Szia!
1-eshez egy kis segítség: gondold úgy végig, hogy n forint hány számra elég? Például 1 ft-ból 1 számból tudod kitalálni a megfelelőt, 2 forintból már 2-ből, 3 ft-ból 3-ból, 4-ből már 5 szám közül... és itt megállnék, mert lelőném a poént. :P Ha így se megy, akkor adok még segítséget, de jobb lenne magadtól rájönni.
|
| Előzmény: [623] Algo, 2008-10-06 16:51:21 |
|
|
| [623] Algo | 2008-10-06 16:51:21 |
 Sziasztok! Íme 2 feladat amivel nem tudok mit kezdeni:
1,Jancsi gondolt egy számra 1 és 32 között. Barchobával kell kitalálni a számot. Jani az igen válaszokért 1 Ft-ot, míg a nem válaszokért 2 Ft-ot kér. Legkevesebb hány Ft-ra lesz szükségünk a szám kitalálásához? Személy szerint 9 Ft-ig jutottam, de tudom hogy nem ez az optimális.
2, Milyen a,b számokra kapunk lineáris becslést a T(n)<=n+T(an)+T(bn) rekurzióból?
Aki meg tudja mondani, annak nagyon szépen megköszönném. Sajnos rengeteget foglalkoztam velük, de nem tudtam mit kezdeni velük. Várom válaszotokat. Előre is köszönöm.
Üdv.:Algp
|
|
| [622] Ali | 2008-10-06 10:37:09 |
 Nem azt akartad írni, hogy
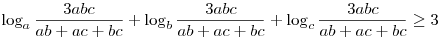
, mert az is igaz ?
A biz. ahogy Jónás elkezdte, utána kihasználni hogy log fv. konkáv, végül pedig a harmonikus és számtani közép közti egyenlőtlenség.
|
| Előzmény: [620] S.Ákos, 2008-10-05 21:37:26 |
|




 2-re kell bebizonyítani.
2-re kell bebizonyítani. 


 d*n minden n<N0-ra. Legyen most
d*n minden n<N0-ra. Legyen most 


