| [75] Doom | 2006-03-25 19:51:48 |
 Ööö nem biztos hogy értem a problémádat, de ha erre gondoltál:
Mivel a3 azt jelenti, hogy a*a*a, így a3=a*a2. Ezt alkalmazva jelen estben is, majd az (n+1)-es szorzót felbontva épp az eredeti azonosság jobb oldalát kapod...
(n+1)3=(n+1)[(n+1)2]=n(n+1)2+(n+1)2
|
| Előzmény: [74] Cybernaut, 2006-03-25 19:07:01 |
|
| [74] Cybernaut | 2006-03-25 19:07:01 |
 Sziasztok!
Az
(n+1)3 = n(n+1)2+(n+1)2
egyenlet megértésében tud valaki segíteni?
Nem tudtam rájönni, hogy az egyenlet jobb oldala milyen összefüggéseken alapul. Miből lehet ezt levezetni?
Azért is hálás lennék ha tudnátok írni olyan linket ahol utána lehet olvasni.
Előre is köszi!
|
|
|
|
| [71] Lóczi Lajos | 2006-01-27 14:32:39 |
 Szerintem ez nagy valószínűséggel be van bizonyítva, mivel a lánctörtre analitikus kifejezés is ismert; a szemifaktoriálisok soráról pedig ezt könnyen el tudom képzelni. Ezt találtam.
Az oldal alján a hivatkozások között lenne érdemes kutakodni a bizonyítások iránt.
|
| Előzmény: [67] Csimby, 2006-01-27 12:45:14 |
|
| [70] Lóczi Lajos | 2006-01-27 13:39:22 |
 Pont ebben a pillanatban akartam én is ugyanezt írni :) Tegnap este nem vettem észre, hogy 2 db 1-essel kezdődik a tört fentről.
Ezért nem Fold[...]-ot, hanem 1/(1+Fold[...])-ot kell írni. Így a kifejezés 2 oldala már 50 tizedesjegyre megegyezik nálam is.
Csimby, próbáld ki a Fold-ot egy a paraméterrel az 1-es szám helyett a Reverse előtt, és rögtön világossá válik a működése (vö. a Help-pel is). Csak előtte a 7000-et vedd le 5-re pl. :)
|
| Előzmény: [68] jonas, 2006-01-27 13:25:55 |
|
|
| [68] jonas | 2006-01-27 13:25:55 |
 Utánaszámoltam én is. A két szélső eredmény stimmel, de nekem a lánctörtre más jött ki:
1/[1+1/(1+2/(1+3/(1+4/(1+5/(1+6/(...))))))] 0.6556795424 0.6556795424
Így kijön az összeg
1.4106861346+0.6556795424=2.0663656771
Szerintem te véletlenül ezt a törtet számoltad helyette:
1/(1+2/(1+3/(1+4/(1+5/(1+6/(...)))))) 0.5251352761 0.5251352761 | (ROSSZ) |
|
| Előzmény: [66] Lóczi Lajos, 2006-01-26 23:54:47 |
|
| [67] Csimby | 2006-01-27 12:45:14 |
 Itt olvastam: Szemjon Grigorjevics Gingyikin: Történetek fizikusokról és matematikusokról 2. javított kiadás (TypoTEX), 396. oldal 3. képlet.
Ismerem a Mathematicát (úgyahogy), de sajnos ezt a Fold-ot még nem használtam, szóval nem teljesen értem, hogy ez mitől lesz az adott lánctört. Csatolom nagyobban is a formulát mert a TeX-es változatban a lánctört nem nagyon látszik...
|
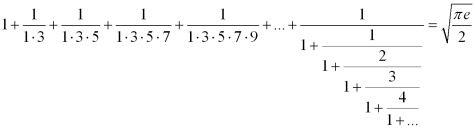 |
| Előzmény: [66] Lóczi Lajos, 2006-01-26 23:54:47 |
|
| [66] Lóczi Lajos | 2006-01-26 23:54:47 |
 Ez egy híres sejtés lenne? Az egyenlőség egyáltalán nem tűnik igaznak, ahogyan azt az alábbi Mathematica-parancs mutatja:
![\sum_{k = 1}^{\infty }\frac{1}{\left( 2k - 1 \right) !!} + {\rm{Fold}}[\left(\frac{\#2}{\#1 + 1}\right) \& , 1, {\rm{Reverse}}[{\rm{Range}}[7000]]]](keplet.cgi?k=C7440DE14B020972)
Itt a lánctörteket 7000 emeletig értékeltem ki, és pl. 40 tizedesjegy pontossággal számoltam. A lánctört értéke stabilizálódni látszik 0.5251352761609812090890905363905787133071 körül [egy-egy emelet hozzáadásakor nő, majd csökken az értéke, úgy viselkedik, mint egy Leibniz-sor]. A végtelen összeg értéke kb. 1.410686134642447997690824711419115041323, így a bal oldal értéke kb. 1.935821410803429206496875309350471575312 -- 40 jegyre.
A jobb oldali gyökös mennyiség viszont kb. 2.066365677061246469234695942149926324723, óriási tehát a különbség.
|
| Előzmény: [65] Csimby, 2006-01-26 20:11:12 |
|






 0.6556795424
0.6556795424