KöMaL Problems in Mathematics, November 2009
Please read the rules of the competition.
Show/hide problems of signs:
 |
Problems with sign 'K'Deadline expired on December 10, 2009. |
K. 223. A bank pays 6% annual interest on fixed deposits. The actual amount paid by the bank is calculated by finding the interest per day (counting 365 days per year), and multiplying by the number of days for which the deposit is fixed. When the locking period is over, the fixed amount is returned to the bank account and the interest is added. In addition, the bank sends letters to the customer informing them about the beginning and the end of the locking period. The letters cost 75 forints each. What is the minimum deposit it is worth fixing for 30 days in this bank? (The bank pays 0% interest on accounts not fixed.)
(6 pont)
solution (in Hungarian), statistics
K. 225. Little Pete is playing with six identical square sheets of plastic on the table. He lays a square on the table, then he lays the next one, always making sure that the newly laid square joins at least one of the previous ones along the full length of an edge. (Vertices always meet vertices.) Show that the perimeters of all those figures obtained that may form the net of a cube unfolded in the plane, is the same.
(6 pont)
solution (in Hungarian), statistics
K. 226. Kate wrote each of the numbers 1, 11, 121, 1331, 14 641 and 161 051 on 10 sheets of paper, and put them in a box. She picked some of the sheets at random, added the numbers on them and got 1 111 111. How many sheets did she pick?
(6 pont)
solution (in Hungarian), statistics
K. 227. Andrew and Bill are preparing for a running race. They train by running around a large regular triangular field several times. They always start simultaneously, and run at uniform speeds. Andrew starts at one vertex, and Bill starts at another. They start running towards each other. Andrew takes 4 minutes and Bill takes 5 minutes to run along one side of the field. Is it possible that they meet at a vertex of the field later on?
(6 pont)
solution (in Hungarian), statistics
K. 228. The length of the diagonal of a cuboid is , where
is a four-digit number. The lengths of the three different edges are three consecutive odd numbers. How long are the edges?
(6 pont)
 |
Problems with sign 'C'Deadline expired on December 10, 2009. |
C. 1005. An intercity train overtakes a freight train travelling on a parallel track. On its way back, the intercity also passes the freight train travelling in the opposite direction. The ratio of the speed of the IC to that of the freight train equals the ratio of the time of overtaking to the time of passing each other in opposite directions. By what factor is the IC faster than the freight train if each train travels at a constant speed?
(5 pont)
solution (in Hungarian), statistics
C. 1006. Prove that six-digit numbers of the form cannot have prime factors of more than two digits.
(5 pont)
solution (in Hungarian), statistics
C. 1007. Prove that the diameter of the inscribed circle of a right-angled triangle is the geometric mean of the difference between the hypotenuse and one leg, and the double of the difference between the hypotenuse and the other leg.
(5 pont)
solution (in Hungarian), statistics
C. 1008. The digits 0, 1, 2, 3, 4, 5, 6 are written in a random order. What is the probability that a seven-digit number divisible by four is obtained? (The number is not allowed to start with zero.)
(5 pont)
solution (in Hungarian), statistics
C. 1009. Given that two perpendicular tangents can be drawn from the origin to the circle x2-6x+y2-2py+17=0, find the possible values of p.
(5 pont)
 |
Problems with sign 'B'Deadline expired on December 10, 2009. |
B. 4212. In a cinema, 80% of the grown-up spectators are men, 40% of the male spectators are children, and 20% of the children are boys. What is the minimum possible number of spectators?
Suggested by J. Pataki, Budapest
(3 pont)
B. 4213. What is the largest possible number of sides of a convex polygon which can be dissected into right-angled triangles with acute angles of 30 and 60 degrees?
(4 pont)
solution (in Hungarian), statistics
B. 4214. We are playing with pawns on a chessboard. The rule is that a pawn is allowed to jump over another to land in a position symmetrical about the pawn it jumped over. Is it possible to transfer nine pawns from the position shown on the left to the position shown on the right in the figure?
(Kvant)
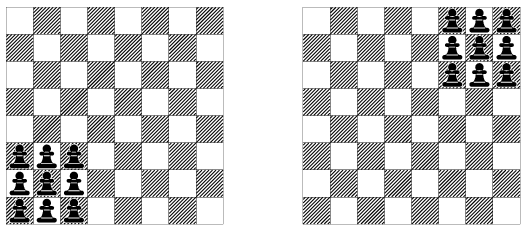
(3 pont)
solution (in Hungarian), statistics
B. 4215. The points \(\displaystyle A\) and \(\displaystyle B\) lie on one side of line \(\displaystyle e\) in the plane. Let \(\displaystyle M\) be the point on the line for which the sum \(\displaystyle AM +MB\) is a minimum, and let \(\displaystyle N\) be the point of the line with \(\displaystyle AN = BN\). Prove that the points \(\displaystyle A\), \(\displaystyle B\), \(\displaystyle M\), \(\displaystyle N\) lie on a circle.
(Kvant)
(4 pont)
solution (in Hungarian), statistics
B. 4216. Find all perfect squares of the form .
(5 pont)
solution (in Hungarian), statistics
B. 4217. Let a, b, c denote the sides of an acute triangle and let 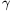 ,
,  ,
,  , respectively, denote the opposite angles (in radians). Show that
, respectively, denote the opposite angles (in radians). Show that .
(4 pont)
solution (in Hungarian), statistics
B. 4218. In a graph, no vertex is connected to all of the others. For any pair of vertices not connected there is a vertex adjacent to both. The sum of the squares of the degrees of vertices is \(\displaystyle n^2-n\) where \(\displaystyle n\) is the number of vertices. What is the length of the shortest possible circuit in the graph?
Suggested by B. Montágh, Memphis
(5 pont)
solution (in Hungarian), statistics
B. 4219. Let \(\displaystyle f\), \(\displaystyle g\), \(\displaystyle h\) be different lines in the space, such that if any line \(\displaystyle e\) in the space that has common points with both \(\displaystyle f\) and \(\displaystyle g\) than also has a common point with \(\displaystyle h\). What can be stated about the mutual position of the lines \(\displaystyle f\), \(\displaystyle g\), \(\displaystyle h\)?
Suggested by G. Mészáros, Kemence
(4 pont)
solution (in Hungarian), statistics
B. 4220. Solve the following simultaneous equations:
\(\displaystyle 1-\frac{12}{3x+y} =\frac{2}{\sqrt{x}},\)
\(\displaystyle 1+\frac{12}{3x+y} =\frac{6}{\sqrt{y}}.\)
Lithuanian competition problem
(4 pont)
solution (in Hungarian), statistics
B. 4221. Let a denote the side of the regular polygon of 18 sides inscribed in a circle of radius r. Show that a3+r3=3ar2.
(4 pont)
 |
Problems with sign 'A'Deadline expired on December 10, 2009. |
A. 491. In the triangle \(\displaystyle A_1A_2A_3\), for each \(\displaystyle i=1,2,3\), the excircle, which is tangent to the side \(\displaystyle A_{i+1}A_{i+2}\), touches the half lines \(\displaystyle A_iA_{i+1}\) and \(\displaystyle A_iA_{i+2}\) at \(\displaystyle P_i\) and \(\displaystyle Q_i\), respectively. (The indices are considered modulo 3, e.g. \(\displaystyle A_4=A_1\) and \(\displaystyle A_5=A_2\).) The lines \(\displaystyle P_iP_{i+1}\) and \(\displaystyle Q_iQ_{i+2}\) meet at \(\displaystyle R_i\); finally, the lines \(\displaystyle P_{i+1}P_{i+2}\) and \(\displaystyle Q_{i+1}Q_{i+2}\) meet at \(\displaystyle S_i\) (\(\displaystyle i=1,2,3\)). Prove that the lines \(\displaystyle R_1S_1\), \(\displaystyle R_2S_2\) and \(\displaystyle R_3S_3\) are concurrent.
(From the idea of Bálint Bíró, Eger)
(5 pont)
A. 492. For every finite, nonempty set \(\displaystyle H\) of positive integers, denote by \(\displaystyle \mathrm{gcd}(H)\) the greatest common divisor of the elements in \(\displaystyle H\). Show that if \(\displaystyle A\) is a finite, nonempty set of positive integers then the following inequality holds:
\(\displaystyle \sum_{\emptyset\ne H\subseteq A} {(-2)}^{|H|-1} \mathrm{gcd}(H) > 0. \)
(5 pont)
A. 493. Prove that
\(\displaystyle \sum_{i=1}^n\ \sum_{j=1}^n \frac{a_ia_j}{{(p_i+p_j)}^c}\ge 0 \)
holds for arbitrary reals \(\displaystyle a_1,a_2,\ldots,a_n\), and positive numbers \(\displaystyle c,p_1,p_2,\ldots,p_n\).
(5 pont)
Upload your solutions above.
