| [757] Kemény Legény | 2005-01-29 10:23:59 |
 Elnézést a közbeszólásért,de szerintem nem ennyi lesz a végeredmény és a megoldás sem ilyen egyszerű.De a legjobb lesz,ha elolvassátok Kós Géza cikkét az 1994/11. KöMaL-ban,ahol egy elég zuzó megoldást nyomat a problémára.
|
|
| [756] Atosz | 2005-01-29 09:53:17 |
 Én a következőképp okoskodtam (remélem jól).
A dobálások után mindenképpen elérjük azt a helyzetet, amikor azt mondhatjuk, hogy innentől akár egy dobással is nyerhetünk. Ekkor 1,2,3...,6 egység távolságra leszünk a 2005. rácsponttól. Az, hogy milyen valséggel állunk éppen az egyik vagy másik helyen, az "jó közelítéssel" egyformán valószínű, azaz 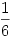 . (az origótól ekkora távolságban már az, hiszen ez a megfelelő távolságra lévő számok 1-6 számok összegeire való felbontások számától függ, ami közel egyforma) Innen a keresett valség . (az origótól ekkora távolságban már az, hiszen ez a megfelelő távolságra lévő számok 1-6 számok összegeire való felbontások számától függ, ami közel egyforma) Innen a keresett valség 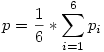
Itt már csak azt kell megvizsgálni, hogy egy adott távolságból hányféleképpen juthatunk célba. pl. 3 egység távolságból bejuthatunk a következő dobásokkal: (3) vagy (1,2) vagy (2,1) vagy (1,1,1). Egy egylépéses győzelem valsége 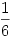 , míg egy k lépésesé , míg egy k lépésesé 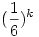 , hiszen k-szor egymás után megfelelőt kell dobnunk. Ha megfigyeljük a megfelelő távolságokról a bejutásokat, akkor látjuk, hogy éppen 6 egylépéses, 15 kétlépéses, 20 háromlépéses, 15 négylépéses, 6 ötlépéses és 1 hatlépéses győzelem van. Ezek a számok éppen a Pascal háromszög megfelelő sorának tagjai (az első 1-es kivételével). Így , hiszen k-szor egymás után megfelelőt kell dobnunk. Ha megfigyeljük a megfelelő távolságokról a bejutásokat, akkor látjuk, hogy éppen 6 egylépéses, 15 kétlépéses, 20 háromlépéses, 15 négylépéses, 6 ötlépéses és 1 hatlépéses győzelem van. Ezek a számok éppen a Pascal háromszög megfelelő sorának tagjai (az első 1-es kivételével). Így
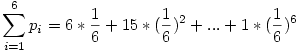
Ami a binomiális tétel szerint ez éppen:
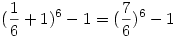
Így a keresett valség:
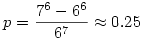
|
| Előzmény: [755] Káli gúla, 2005-01-27 23:18:19 |
|
| [755] Káli gúla | 2005-01-27 23:18:19 |
 Kösz. Én is a rekurziót oldottam meg először.
Erről eszembe jut egy feladat, szintén valszám, és szintén rekurzió, Amikor először hallottam, talán egy egész spirálfüzetet teleírtam, de nem tudtam megcsinálni. Évek múlva jöttem csak rá az "igazi" megoldásra.
144. feladat. Az origóból kiindulva a számegyenes pozitív rácspontjain lépkedünk. Minden lépés előtt feldobunk egy dobókockát, és annyit lépünk előre, amennyit a kocka mutat. Mi a valószínűsége (jó közelítéssel) annak, hogy rálépünk a 2005. rácspontra.
|
|
| [754] jenei.attila | 2005-01-27 21:06:27 |
 Szóval én úgy értelmezem Káli gúla modelljét, hogy kitüntetjük az őrültek helyét, és az utolsó helyet (feltesszük, hogy az utolsó utas nem őrült). Egy kísérlet abban ál, hogy beszállítjuk az összes utast, miközben feljegyezzük, hogy a kitüntetett helyeket milyen sorrendben foglalták el. Nyilván akkor ül az utolsó utas a helyére, ha az utolsó helyet jegyeztük fel utoljára. Egy kísérlet tehát a kitüntetett helyek permutációját adja, amelyek ha egyenlő valószínűséggel fordulnak elő, akkor az utolsó utas valóban 1/(k+1) valséggel ül a helyére. Az hogy ezek a permutációk egyenlő valószínűséggel fordulnak elő, azon múlik, hogy a kitüntetett még el nem foglalt helyek bármelyikét minden pillanatban amikor kitüntetett helyet foglal el egy utas, egyenlő valószínűséggel választja.
Káli gúlának gratulálok ehhez a megoldáshoz, az enyém sokkal körülményesebb. Csak az lenne a kérdésem, ha nem ismerted volna az eredményt, akkor is ezt a megoldást adtad volne-e?
|
| Előzmény: [753] Kós Géza, 2005-01-27 17:01:18 |
|
|
|
| [751] Atosz | 2005-01-27 14:35:01 |
 Kedves attila!
Örülök, hogy tőlem kérsz segítséget, én amikor először találkoztam a feladattal, akkor tulajdonképpen ugyanazt az utat követtem végig, mint te. Káli gúla modelljén most gondolkodom, majd írok. Minden jót!
Atosz
|
| Előzmény: [750] jenei.attila, 2005-01-27 12:28:13 |
|
| [750] jenei.attila | 2005-01-27 12:28:13 |
 Kedves Atosz és Géza!
Segítenétek nekünk? Lehet hogy nekem nehéz a felfogásom, de még mindig nem látom Káli gúla modelljének helyességét. Egy őrült esetén (akiről feltesszük hogy az első utas), ha ő rögtön a saját helyére ül, az a modellben azt jelenti, kihúztuk a fehér golyót. A modellben ez 1/2 valségű esemény, míg az eredeti feladatban 1/n. Szerintem nem ugyanazok az eseményterek (pontosabban nem felelnek meg egymásnak). Géza te nyilván valami rafinált trükkre gondoltál, amellyel sokkal egyszerűbben oldható meg a feladat. Kicsit segítenél ebben? Atosz, te is így gondoltad a k őrült esetét megoldani, ahogy én csináltam?
|
|
| [749] jenei.attila | 2005-01-27 12:14:30 |
 Ezek szerint csak az számít húzásnak, ha az őrült a saját helyére ül, vagy az utolsóra. De honnan tudjuk, hogy ezek a húzások egyenlően valószínűek. A Te modelledben igen, de az eredeti feladatban miért is?
|
| Előzmény: [748] Káli gúla, 2005-01-27 12:06:52 |
|
| [748] Káli gúla | 2005-01-27 12:06:52 |
 Kedves attila
A k+1 kitüntetett hely mellett a többi "normális" helyet úgy képzelem, mintha dobókockával érvénytelent dobnánk: a kocka az "élére" esne, vagy legurulna az asztalról.
k=1 őrültre a legegyszerűbb (ezt Géza figyelmeztetése előtt is láttam):
(1) Ha az örült a saját helyére ül, akkor a játék eldőlt, az utolsó utas nyer. (2) Ha az örült az utolsó utas helyére ül, akkor a játék eldőlt, az utolsó utas vesztett. (3) Minden más esetben nem történt semmi, "új őrült jön" (ld. elgurult dobókocka, vagy élére esett pénz).
|
| Előzmény: [747] jenei.attila, 2005-01-27 10:36:07 |
|
|
| [746] Káli gúla | 2005-01-27 10:22:12 |
 Egy urnában k fehér és 1 fekete golyó van. Sorban kihúzzuk az összes golyót. Legyen p annak a valószínűsége, hogy utoljára fekete golyót húzunk. Ha az eseményt visszafelé történtnek képzeljük, akkor p annak a valószínűsége is, hogy ezeket a golyókat sorban az urnába dobálva elsőre fekete golyót dobunk be, azaz p=1/(k+1).
(Az őrült utasok ülései a fehér golyók, az utolsó utas ülése a fekete golyó.)
|
| Előzmény: [743] Kós Géza, 2005-01-26 18:09:47 |
|
| [745] Kós Géza | 2005-01-26 18:21:09 |
 Egy rokon feladat.
143. / B. 3391. Amikor Bendegúz érvényes helyjegyével felszállt a 78 személyes vasúti kocsiba, döbbenten vette észre, hogy ott már minden hely foglalt. Az történt ugyanis, hogy Dömötör helyjegy nélkül szállt fel. A többi 77 utas pedig - köztük Elek - vásárolt ugyan helyjegyet, de nem feltétlenül ültek oda, ahová a helyjegyük szólt. Bendegúz felállítja azt, aki a helyét elfoglalta. Aki feláll, az most már szintén a saját helyére szeretne leülni, és így tovább. Mindez addig folytatódik, míg végül Dömötör lelepleződik. Mennyi a valószínűsége annak, hogy Elek ülve nézheti végig az eseményeket?
(KöMaL, 2000. december)
|
| Előzmény: [743] Kós Géza, 2005-01-26 18:09:47 |
|
|
|
| [742] Atosz | 2005-01-26 17:43:41 |
 Sziasztok!
Itt az újabb példa, szintén a valség köréből (A feladat Mikulás-probléma néven is ismert).
Egy 'n' fős osztályban Mikulás ünnepségre készülnek a gyerekek. A tanár mindenkinek felírja a nevét egy cetlire, majd beteszi egy kalapba és ezután kezdődik a húzás. Miután mindenki kihúzott egyet, mi a valószínűsége annak, hogy senki sem húzta a saját nevét, azaz nem kell kezdeni mindent előről?
|
|
| [741] jenei.attila | 2005-01-24 16:30:06 |
 Kiegészítés: előzőleg külön kezeltük azt az esetet, amikor az utolsó utas őrült, mondván, hogy a keresett valószínűség ekkor ugyanaz, mint amikor k-1 őrült van. Ugyanis nem befolyásolja az eseményeket, hogy az utolsó utas őrült vagy sem, mivel csak az egyetlen megmaradt helyre tud ülni. Összefoglalva tehát: n utas és ezek közül bármely k őrült utas esetén (n>=k) annak valószínűsége hogy az utolsó utas a helyére ül 1/(k+1), ha az utolsó utas nem őrült, és 1/k, ha az utolsó utas őrült.
|
| Előzmény: [740] jenei.attila, 2005-01-24 15:53:03 |
|
| [740] jenei.attila | 2005-01-24 15:53:03 |
 Tegyük fel, hogy n utas van, és ezek közül az i1,i2,...,ik (ahol 1<=i1<i2<...<ik<=n) sorszámú utasok őrültek. Jelöljük pn(i1,i2,...,ik)-val annak valószínűségét, hogy az utolsó utas a helyére tud ülni. Tegyük fel, hogy a szóban forgó valószínűségeket már ismerjük n-nél kevesebb utas és ezek közül bármely k,k-1,k-2,...,1 őrült esetén. Világos, hogy ekkor már csak a pn(1,i2,...,ik) alakú valószínűségeket kell kiszámolni, mivel i1>1 esetén a keresett valószínűség pn-i1+1(1,i2-i1+1,...,ik-i1+1) (hiszen az első i1-1 utasig rendben mennek a dolgok), amit a feltevés szerint már ismerünk. Természetesen ahhoz, hogy egyáltalán ilyen módon k őrült esetén el tudjunk indulni, ismerni kell a pk+1(1,i2,...,ik) valószínűségeket (ha i1<>1, akkor pk+1(2,3,...,k+1)=pk(1,2,...,k)=pk(1,2,...,k-1) valószínűségről van szó, mivel mindegy hogy az utolsó utas őrült -e vagy sem, úgyis csak az egyetlen üres helyre tud ülni). A továbbiakban egyszerűsítjük a jelölést, mivel indukcióval feltesszük, hogy k-nál kevesebb őrült esetén a valószínűség független attól, hogy pontosan mely utasok őrültek, vagyis pn,m:=pn(i1,...,im) bármely i1,...,im kombináció esetén. Mint azt egy őrült esetén láttuk, a feltevés jogos. Tehát van k+1 utasunk, az első k utas őrült. Feltehetjük, hogy az utolsó utas nem őrült, mert ez nem befolyásolja a keresett valószínűséget (így is úgy is csak az egyetlen megmaradt helyre tud ülni), ha pedig őrült lenne, akkor nyilván eggyel kevesebb őrülttel kellene megoldani a feladatot, amit már a feltevés szerint megoldottunk. Ekkor
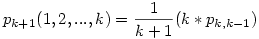
. A fenti képletben az 1. utas (aki őrült) 1/(k+1) valószínűséggel ül bármely helyre. Ha saját vagy másik őrült helyére ül, akkor a leültetendő utasok és az őrültek száma 1-gyel csökken, ezt nyilván k féleképpen teheti meg. Az egyetlen normális utas (utolsó utas) helyére nem ülhet, mert akkor biztos hogy az utolsó utas nem ül a saját helyére. Most teljes indukcióval feltesszük, hogy minden n-re, és minden m<k őrültre a keresett valószínűség 1/(m+1). Ez m=1-re már bizonyított. Ekkor a fenti képlet szerint
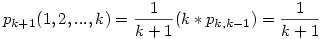
. Most rögzített k őrültszám mellett n szerinti teljes indukcióval haladunk (n>k), és feltesszük, hogy adott k mellett n-1,n-2,...,k+1 utassal a keresett valószínűség utasszámtól és őrültek kombinációjától függetlenül 1/(k+1).
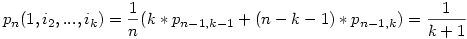
. Az első utas (aki őrült) 1/n valószínűséggel ül bármely helyre, ebből k esetben őrült helyére (a sajátját is beleértve). Ha őrült helyére ült, akkor az utasok és az őrültek száma is 1-gyel csökken, mely esetre ismerjük a valószínűséget (1/k). Ha nem őrült helyére és nem is az utolsó helyre ül (n-k-1 eset), akkor az utasok száma 1-gyel csökken, de akinek a helyére ült, az megőrül, vagyis az őrültek száma marad. Az indukciós feltevés szerint ez esetekben is ismerjük a valószínűséget (1/(k+1)). Innen n utasra és k őrültre (ahol az 1. utas biztos őrült) a keresett valószínűség 1/(k+1) és független az őrültek kombinációjától, ha n-nél kevesebb utasra is fügetlen volt (ez az indukciós feltevés).
|
|
| [739] Kemény Legény | 2005-01-23 20:20:23 |
 Egy nem túl pontos,de elvi becslés a p(k,n) valószinűségre: p(k,n) legfeljebb k/(n+k).Ez (2k+n) szerinti teljes indukcióval triviális. k=0 esetén 0 pontos,k=1 esetén 1/(n+1) pontos,k=2 esetén 2/(n+2),ami nincs messze a pontostól.Sajnos ez csak 'soronként' becsül,azaz csak a nyilvánvaló állitás jön ki,hogy hogy ha felek száma végtelenbe tart,akkor a valószinűség 0-hoz.Sajnos az 'érdekes' p(n,0) határértékről semmit sem mond( csak azt, hogy p(n,0)<1).
|
|
| [738] Atosz | 2005-01-23 15:21:35 |
 Kedves jenei.attila!
Gratulálok a megoldásaidhoz, bár szerintem jó lenne, ha megpróbálnád leírni. (TeX-el vagy nélküle...)
Gyógyszer...
Sikerült a pk,k-hoz hasonló zárt, de sajnos rekurzív képletet felírnom pe,f-re, hátha valamelyikőtöknek sikerül vele valamit kezdeni:
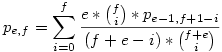
Sok szerencsét az alakítgatásához!
Kedves Kós Géza!
Küldtem neked emilt a honlapodon lévő e-mail címekre. Légyszi nézd meg őket, és írj vissza valamit. Előre is köszönöm!
|
| Előzmény: [737] jenei.attila, 2005-01-22 18:34:34 |
|
| [737] jenei.attila | 2005-01-22 18:34:34 |
 Hasonló gondolatmenettel belátható, hogy k őrült esetén a keresett valószínűség 1/(k+1), ha az emberek száma legalább k+1. Érdekes megfigyelni, hogu a valószínűség nem függ n-től, és attól sem, hogy mely utasok őrültek. Ezt teljes indukcióval lehet igazolni, de leírni kicsit bolnyolult.
|
| Előzmény: [736] Atosz, 2005-01-21 11:14:45 |
|
| [736] Atosz | 2005-01-21 11:14:45 |
 Kedves rizs!
jenei.attila megoldása teljesen jó (és így "hivatalos" is), legfeljebb a vége egy picit elnagyolt.
Amiből kiindulunk az a:
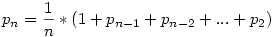
Ez ugye azt jelenti, hogy minden helyre 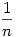 valséggel ül, a zárójelben pedig sorra 1, ha a saját helyére, pn-1 ha a második helyére stb... valséggel ül, a zárójelben pedig sorra 1, ha a saját helyére, pn-1 ha a második helyére stb...
Ha felírjuk ugyanezt n-1 emberre, akkor kapjuk, hogy:
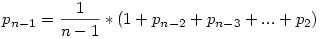
Így az első sorban a zárójelben lévő 1+pn-2+...p2 helyére beírhatjuk, hogy (n-1)*pn-1 és kapjuk, hogy
n*pn=n*pn-1
Ez azt jelenti, hogy minden pi egyforma, azaz 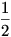
Persze még hiányzik az n utas és k őrült esete.
|
| Előzmény: [734] rizs, 2005-01-20 23:21:37 |
|
| [735] Kemény Legény | 2005-01-21 10:54:00 |
 Ami a határértéket illeti,fogalmam hogy sincs hogy mennyi,vagy hogy létezik-e,de az biztos hogy ha létezik a p(n,0) határérték(n tart végtelenhez),akkor minden rögzitett a esetén létezik a p(n,a) határérték és egyenlő a p(n,0) határértékével(legyen ez P).Ugyanis p(n,0)=p(n-1,1) igy a=1 esetén igaz. Indukcióval p(n,a)=p(n-1,a+1)(n/(n+a))+p(n,a-1)(a/(n+a)) A baloldal P-hez tart, a jobb oldal 2.tagja 0-hoz tart,mert a/(n+a) 0-hoz tart,mig n/(n+a) 1-hez tart,igy p(n,a) határértéke egyenlő p(n-1,a+1) határértékével,igy a p(n,a+1) határértéke egyenlő p(n,a+1) határértékével.
|
| Előzmény: [733] Atosz, 2005-01-20 21:35:33 |
|
| [734] rizs | 2005-01-20 23:21:37 |
 Kedves Attila!
Az őrült emberes feladat "hivatalos" megoldását meg lehet tudni?
|
|
| [733] Atosz | 2005-01-20 21:35:33 |
 Sziasztok!
Megnéztem az Excell által készített pe,f valószínűségi adatokat e és f eseteiben 0-60-ig. A kapott eredmények alátámasztják az előző feltevésemet.
A p1,f, p2,f,.. valószínűségek ahogy 1-1 egész szemet hozzáveszünk növekednek egészen e=f-ig, majd e>f esetén már csökkennek.
p60,0=0,1556486 ám a csökkenése p59,0-hoz képest mindössze 5 tízezred. Ha elindulunk egy kicsit feljebb úgy, hogy a szemek száma 60 maradjon pl. p30,30=0,14771909 és p18,42=0,13021446
Ha messziről nézem a pe,0 grafikont, akkor az úgy néz ki mint egy hiperbola.
p2,k közelítése 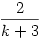 -al nagyon pontosnak tűnik a megfelelő érték eltérése a közelítéstől k=58 esetében mindössze 15 tízezred. Ez is a hiperbola jelleget támasztja alá. -al nagyon pontosnak tűnik a megfelelő érték eltérése a közelítéstől k=58 esetében mindössze 15 tízezred. Ez is a hiperbola jelleget támasztja alá.
Minden jót: Atosz
|
|





