KöMaL Problems in Mathematics, February 2007
Please read the rules of the competition.
Show/hide problems of signs:
 |
Problems with sign 'K'Deadline expired on March 16, 2007. |
K. 115. When more than one files are selected on the computer for copying at the same time, and the process of copying is started, there are two progress bars displayed. The upper one shows what percentage of the file just being copied is done and the lower one shows what percentage of the whole copying task is done (including the files copied before the current file). Suppose there are three files copied in this way. When the first file is being copied and the upper progress bar reads 35%, the lower bar reads 14%. When the upper bar reads 24% during the copying of the second file, the lower bar reads 46%. What does the upper progress bar read when the lower one reads 72%? (The given data are exact values, not approximations.)
(6 pont)
solution (in Hungarian), statistics
K. 116. Let us make 3×3 Latin squares out of a deck of French cards. (There is a card in each field of the Latin square.) Number cards are worth the value printed on them; jacks, queens, kings and aces are worth 11, 12, 13 and 1, respectively. In a Latin square, the sum of the numbers is the same in each row, column and diagonal. Let us call this equal sum the ``magic number'' of the square.
a) What is the largest possible magic number that can be achieved if all the nine cards used are clubs?
b) Is there a square whose magic number is 37 if any 9 cards may be used?
(6 pont)
solution (in Hungarian), statistics
K. 117. A sheet of paper is folded in three along the dotted lines as shown in the Figure. (Each crease may have an arbitrary direction.) The creases divide the two sides of the sheet into six parts altogether. Each of the six parts is coloured in a different colour, and the sheet is folded again along the original lines. Then there will be only two parts that can be seen. How many different pairs of colours may result from different ways of folding the sheet?
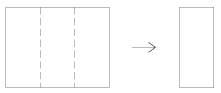
(6 pont)
solution (in Hungarian), statistics
K. 118. Find all five-digit numbers , such that there are exactly a zeros, b ones, c twos, d threes and e fours among the digits. (Different letters do not necessarily denote different digits.)
(6 pont)
solution (in Hungarian), statistics
K. 119. There are two tribes living in Binumeria. The difference between the two tribes is that they write numbers in notations using different bases. A member of each tribe was asked how many members their tribe had. Each of them answered . How many inhabitants are there in Binumeria, given that each tribe consists of more than 100 but less than 1000 members?
(6 pont)
solution (in Hungarian), statistics
K. 120. a) Find a solid bounded by polygonal faces that has 12 vertices and 18 edges.
b) Is there a solid bounded by polygonal faces that has 12 vertices and 16 edges?
(6 pont)
 |
Problems with sign 'C'Deadline expired on March 19, 2007. |
C. 885. The charge of money withdrawal from an ATM is made up of two terms. There is a flat charge independent of the amount withdrawn and another part that is proportional to it. For forints (Hungarian currency, HUF) withdrawn the charge is 221 forints, and for
it is 485 forints. What is the charge for
forints?
(5 pont)
solution (in Hungarian), statistics
C. 886. The wall of a building is decorated by a square with its circumscribed circle drawn. There is a semicircle drawn outwards on each side of the square as a diameter, so that the circular arcs form four crescent shaped figures. What is the length of the side of the square if the area of such a crescent is 1 m2?
(5 pont)
solution (in Hungarian), statistics
C. 887. How many eight-digit numbers are there in which every digit occurs the same number of times as the value of the digit? (Example: .)
(5 pont)
solution (in Hungarian), statistics
C. 888. The measures of the volume and the surface area of a cube with edges of 6 unit lengths are both 216. Find all square based prisms of integer edges that have this property.
(5 pont)
solution (in Hungarian), statistics
C. 889. The Figure shows a truncated pyramid of rectangular bases and height m, viewed from above. Someone found the following formula for the volume of the truncated pyramid:
Is this formula correct?
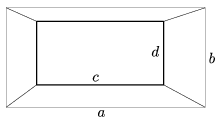
(5 pont)
 |
Problems with sign 'B'Deadline expired on March 19, 2007. |
B. 3972. Let n be a positive integer. Prove that there exist n integers such that their sum is 0 and their product is n if and only if n is divisible by 4.
(3 pont)
solution (in Hungarian), statistics
B. 3973. In how many different ways is it possible to place 14 bishops on a chessboard so that they do not attack each other?
(3 pont)
solution (in Hungarian), statistics
B. 3974. Given a triangle ABC. Find the locus of the points P in the plane for which AP2+BP2=CP2?
(4 pont)
solution (in Hungarian), statistics
B. 3975. N and k are positive integers. We have counted the different ways of expressing N in the form a+b+c, where 1 a,b,c
a,b,c k, and the order of the terms also matters. Is it possible that we got 2007?
k, and the order of the terms also matters. Is it possible that we got 2007?
(5 pont)
solution (in Hungarian), statistics
B. 3976. Through an interior point of a triangle of sides a, b, c a parallel line is drawn to each side. Given that the segments of these lines intercepted by the triangle have the same length, find that length.
(4 pont)
solution (in Hungarian), statistics
B. 3977. Solve the following simultaneous equations on the set of positive real numbers: x2+xy+y2=2, y2+yz+z2=5, z2+xz+x2=3.
(4 pont)
solution (in Hungarian), statistics
B. 3978. Prove that the following relationship is true in every triangle: 2R(sa+sb+sc) a2+b2+c2. (where a, b, c are the sides, sa, sb, sc are the lengths of the medians and R is the radius of the circumscribed circle.)
a2+b2+c2. (where a, b, c are the sides, sa, sb, sc are the lengths of the medians and R is the radius of the circumscribed circle.)
(5 pont)
solution (in Hungarian), statistics
B. 3979. The vertices of triangle ABC are labelled in counterclockwise order. The angles at the vertices A, B, and C are  ,
,  and
and 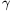 , respectively. The vertex B is rotated about the point A through the angle
, respectively. The vertex B is rotated about the point A through the angle  in clockwise direction. The point B1 obtained is rotated about B through the angle
in clockwise direction. The point B1 obtained is rotated about B through the angle  in clockwise direction. Finally, the point B2 obtained is rotated about C in clockwise direction to the point B3. Given the points B, B3 and O the middle point of the incentre of the triangle ABC, construct the triangle. Investigate how the solution depends on the positions of the three given points.
in clockwise direction. Finally, the point B2 obtained is rotated about C in clockwise direction to the point B3. Given the points B, B3 and O the middle point of the incentre of the triangle ABC, construct the triangle. Investigate how the solution depends on the positions of the three given points.
(Based on a problem from the National Mathematics Competition for Secondary Schools (OKTV))
(4 pont)
solution (in Hungarian), statistics
B. 3980. The Figure shows a polyhedron viewed from above. Its ``bases'' are parallel rectangles, its lateral edges are equal in length, and its height is m. Someone found the following formula for the volume of the polyhedron:
Is the formula correct?
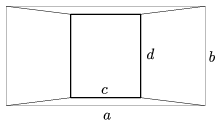
(3 pont)
solution (in Hungarian), statistics
B. 3981. The real numbers ai, bi () satisfy the following inequalities:
, and
, if 1
 k
k n. Prove that
n. Prove that .
(5 pont)
 |
Problems with sign 'A'Deadline expired on March 19, 2007. |
A. 419. The diagonals of a cyclic quadrilateral ABCD meet at X. The circles ABX and CDX meet again at Y. Take point Z such that triangles BZC and AYD are similar. Show that if BZCY is convex, then it has an inscribed circle.
(Russian competition problem)
(5 pont)
A. 420. Find all functions such that |f(x)-f(y)|
 |x-y| for all x,y>0 and there exist positive constants a, b, c satisfying
|x-y| for all x,y>0 and there exist positive constants a, b, c satisfying
for all x.
(Proposed by Edgár Dobribán, Cluj-Napoca (Romania))
(5 pont)
A. 421. Find positive constants  and c such that
and c such that
holds for all positive integer N.
(5 pont)
Upload your solutions above.
